
- •Действия с матрицами
- •Как можно отблагодарить автора?
- •Как вычислить определитель?
- •Как можно отблагодарить автора?
- •Свойства определителя. Понижение порядка определителя
- •Эффективные методы вычисления определителя
- •Определитель выгоднее раскрывать по той строке (столбцу), где:
- •Свойства определителя
- •При транспонировании матрицы величина её определителя не меняется
- •Если две строки (или два столбца) определителя поменять местами, то определитель сменит знак
- •Из строки (столбца) определителя можно вынести общий множитель
- •Если две строки (столбца) определителя пропорциональны (как частный случай – одинаковы), то данный определитель равен нулю
- •Определитель с нулевой строкой (столбцом) равен нулю
- •Какие свойства определителей полезно знать?
- •Понижение порядка определителя
- •К строке определителя можно прибавить другую строку, умноженную на ненулевое число. При этом величина определителя не изменится
- •К столбцу определителя можно прибавить другой столбец, умноженный на ненулевое число. При этом величина определителя не изменится
- •Как можно отблагодарить автора?
- •Как найти обратную матрицу?
- •Как можно отблагодарить автора?
- •Некоторые свойства операций над матрицами. Матричные выражения
- •Некоторые свойства операций над матрицами
- •Можно ли к матрице прибавить число?
- •Как возвести матрицу в квадрат?
- •Немного о некоммутативности матричного умножения и единичной матрице
- •Коммутативность числового множителя относительно умножения матриц
- •Как умножить три матрицы?
- •Как возвести матрицу в куб и более высокие степени?
- •Матричные выражения
- •Как можно отблагодарить автора?
- •Матричные уравнения. Примеры решений
- •Общие принципы решения матричных уравнений
- •Как решить матричное уравнение?
- •Как выполнить проверку?
- •Распространённый алгоритм решения матричного уравнения
- •Решение матричного уравнения вида
- •Решение матричного уравнения вида
- •Как можно отблагодарить автора?
- •Как решить систему линейных уравнений?
- •Решение системы линейных уравнений методом подстановки
- •Решение системы методом почленного сложения (вычитания) уравнений системы
- •Как можно отблагодарить автора?
- •Как решить систему линейных уравнений?
- •Решение системы линейных уравнений методом подстановки
- •Решение системы методом почленного сложения (вычитания) уравнений системы
- •Как можно отблагодарить автора?
- •Правило Крамера. Метод обратной матрицы
- •Решение системы по формулам Крамера
- •Решение системы с помощью обратной матрицы
- •Как можно отблагодарить автора?
- •Метод Гаусса (последовательного исключения неизвестных). Примеры решений для чайников
- •Как можно отблагодарить автора?
- •Решение систем линейных уравнений. Несовместные системы. Системы с общим решением. Частные решения
- •Как можно отблагодарить автора?
- •Как найти ранг матрицы?
- •Что такое ранг матрицы?
- •Как найти ранг матрицы с помощью миноров?
- •Алгоритм нахождения ранга матрицы с помощью миноров
- •Метод окаймляющих миноров
- •Как найти ранг матрицы с помощью метода Гаусса?
- •Какой метод использовать для нахождения ранга матрицы?
- •Как исследовать систему линейных уравнений на совместность?
- •Как можно отблагодарить автора?
- •Однородные системы линейных алгебраических уравнений
- •Что такое однородная система линейных уравнений?
- •Фундаментальная система решений однородной системы уравнений
- •Взаимосвязь решений неоднородной и соответствующей однородной системы уравнений
- •Как можно отблагодарить автора?
- •Метод Жордано-Гаусса. Как найти обратную матрицу с помощью элементарных преобразований?
- •Как найти обратную матрицу методом Гаусса?
- •Как можно отблагодарить автора?
- •Решение системы при различных способах выбора базиса
- •Как можно отблагодарить автора?
- •Собственные значения (числа) и собственные векторы. Примеры решений
- •Сколько у матрицы собственных чисел и собственных векторов?
- •Как найти собственные значения и собственные векторы матрицы?
- •Найти матрицу в базисе из собственных векторов
- •Как решать задачу в случае кратных собственных чисел?
- •Собственные векторы – это в точности векторы фундаментальной системы решений
- •Как можно отблагодарить автора?
- •Комплексные числа для чайников
- •Понятие комплексного числа
- •Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел
- •Тригонометрическая и показательная форма комплексного числа
- •Возведение комплексных чисел в степень
- •Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями
- •Как можно отблагодарить автора?
Решение матричного уравнения вида
Алгоритм решения точно такой же с некоторыми содержательными и техническими отличиями:
Пример 5
Решить матричное уравнение, выполнить
проверку найденного решения.
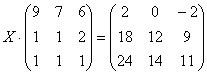
Решение: Уравнение имеет готовый вид , что позволяет сразу же заняться «иксом».
Для разрешения уравнения относительно
умножим
обе его части на
справа:
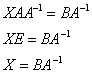
При оформлении можно записать и короче:
«Решение ищем в виде ![]() ».
».
Матрица «бэ» известна. Берём матрицу 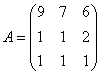 и
без комментариев исследуем обратную
сторону Луны:
и
без комментариев исследуем обратную
сторону Луны:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
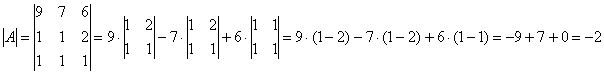
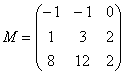 –
матрица миноров соответствующих
элементов матрицы
.
–
матрица миноров соответствующих
элементов матрицы
.
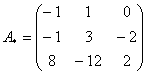 –
матрица алгебраических дополнений.
–
матрица алгебраических дополнений.
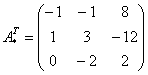 –
транспонированная матрица алгебраических
дополнений.
–
транспонированная матрица алгебраических
дополнений.
Таким образом, обратная матрица:
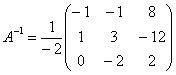 Находим
решение, при этом не забываем
про порядок умножения матриц,
обратная матрица едет во втором вагоне:
Находим
решение, при этом не забываем
про порядок умножения матриц,
обратная матрица едет во втором вагоне:
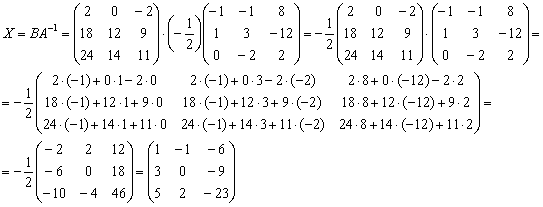
Ответ: 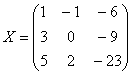
Проверка: Подставим найденное значение
в
левую часть исходного уравнения:
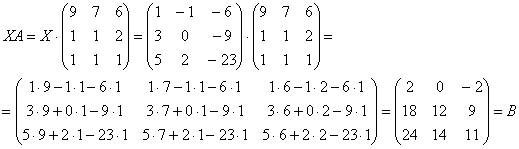
Получена правая часть исходного уравнения. Таким образом, решение найдено правильно.
Усложним задание:
Пример 6
Решить матричное уравнение, сделать
проверку:
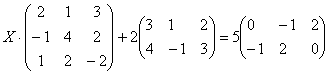
Решение: Незнакомец расположился слева от матрицы, поэтому уравнение сводится к виду . Упаковываем множители, переносим свободную матрицу в правую часть и выполняем вычитание матриц:
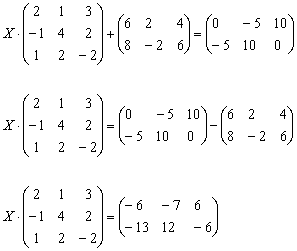
Для разрешения уравнения относительно умножим обе его части на справа:
Обратную матрицу найдем по формуле: , где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
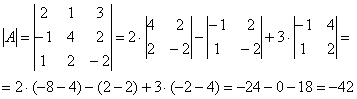
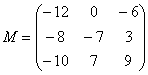 –
матрица миноров соответствующих
элементов матрицы
.
–
матрица миноров соответствующих
элементов матрицы
.
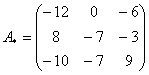 –
матрица алгебраических дополнений.
–
матрица алгебраических дополнений.
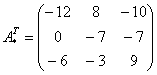 –
транспонированная матрица алгебраических
дополнений.
–
транспонированная матрица алгебраических
дополнений.
Обратная матрица:
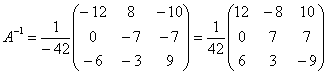
Здесь целесообразно внести минус в матрицу. Возможно, вам надоела однообразная картинка с нахождением обратной матрицы в каждом примере, я бы вполне мог пропускать данный пункт и сразу записывать: «обратная матрица такая-то…». Нет, полное решение приводится не случайно. Это отличная возможность потренироваться! Кроме того, у некоторых студентов действительно очень низкий уровень подготовки и полный трафарет того или иного примера будет как нельзя кстати. Да и сам Гугл, глядишь, научится решать матричные уравнения =)
Находим решение:
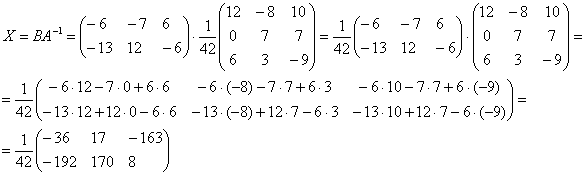
Ответ: ![]()
Проверка: Подставим найденное значение
в
левую часть исходного уравнения:
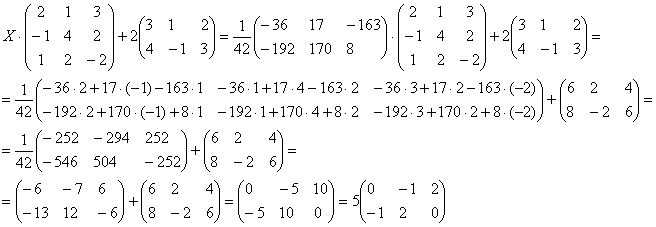 Получена
правая часть исходного уравнения, таким
образом, решение найдено верно.
Получена
правая часть исходного уравнения, таким
образом, решение найдено верно.
Пример 7
Решить матричное уравнение и сделать
проверку:
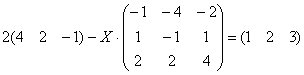
Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.
В заключение коротко рассмотрим ещё
один тип матричного уравнения, который
практически не встречается:
,
где ![]() –
известные матрицы. То есть, наш партизан
залёг между двумя матрицами.
–
известные матрицы. То есть, наш партизан
залёг между двумя матрицами.
Разрешим данное уравнение относительно
.
Сначала умножим обе части на
слева:
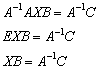
Теперь умножим обе части на ![]() справа:
справа:
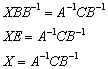
Готового примера у себя в коллекции я
не нашёл, но сейчас всё равно что-нибудь
подберу из этой оперы…. Вот:
![]()
Да, работёнки здесь побольше. Раза в два. Как решить данное уравнение?
– для матрицы ![]() находим
обратную матрицу
;
–
для матрицы
находим
обратную матрицу
;
–
для матрицы ![]() находим
обратную матрицу
;
–
перемножаем три матрицы
находим
обратную матрицу
;
–
перемножаем три матрицы ![]() (см.
статью про свойства
матричных операций).
(см.
статью про свойства
матричных операций).
Желающие могут прорешать данный пример,
верный ответ: ![]() .
.
Поздравляю ещё раз! Если вы читаете эти строки, то Конец Света так и не наступил! Конец Света как деньги – любит тишину =) На самом деле всё было так: летописцы майя составили свой календарь до дня зимнего солнцестояния 2012 года. А потом устали.
Но на всякий случай передаю привет следующей цивилизации. Когда-нибудь они откопают хорошо сохранившийся в вечной мерзлоте сервер и расшифруют нашу клинопись =)
Удачной сдачи зачётов и экзаменов!
Решения и ответы:
Пример 4: Решение:
Приведем уравнение к виду
:
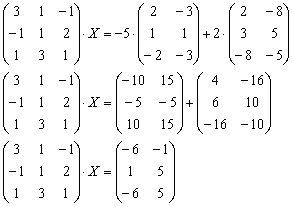 Для
разрешения уравнения относительно
умножим
обе его части на
слева:
Обратную
матрицу найдем по формуле:
,
где
–
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
.
Для
разрешения уравнения относительно
умножим
обе его части на
слева:
Обратную
матрицу найдем по формуле:
,
где
–
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
.
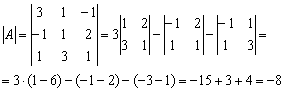
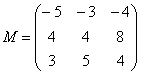 –
матрица миноров соответствующих
элементов матрицы
.
–
матрица миноров соответствующих
элементов матрицы
.
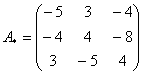 –
матрица алгебраических дополнений.
–
матрица алгебраических дополнений.
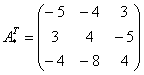 –
транспонированная матрица алгебраических
дополнений.
Обратная
матрица:
–
транспонированная матрица алгебраических
дополнений.
Обратная
матрица:
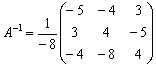 Решение
системы:
Решение
системы:
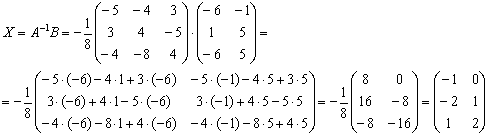 Ответ:
Ответ: 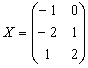 Проверка:
подставим найденное значение
в
левую часть исходного уравнения:
Проверка:
подставим найденное значение
в
левую часть исходного уравнения:
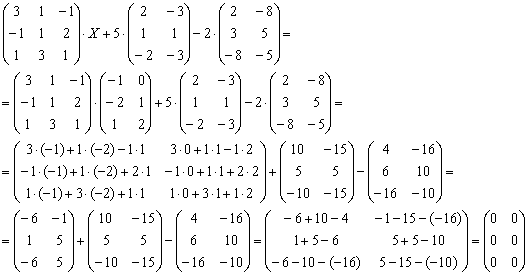 Получена
правая часть исходного уравнения, таким
образом, значение
найдено
верно.
Получена
правая часть исходного уравнения, таким
образом, значение
найдено
верно.
Пример 7: Решение:
Приведем уравнение к виду
:
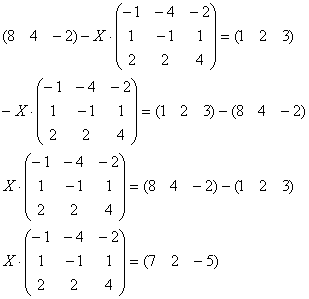 Для
разрешения уравнения относительно
умножим
обе его части на
справа:
Обратную
матрицу найдем по формуле:
,
где
–
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
.
Для
разрешения уравнения относительно
умножим
обе его части на
справа:
Обратную
матрицу найдем по формуле:
,
где
–
транспонированная матрица алгебраических
дополнений соответствующих элементов
матрицы
.
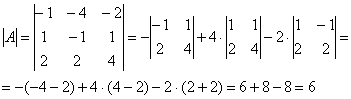
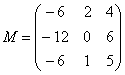 –
матрица миноров соответствующих
элементов матрицы
.
–
матрица миноров соответствующих
элементов матрицы
.
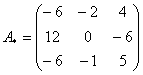 –
матрица алгебраических дополнений.
–
матрица алгебраических дополнений.
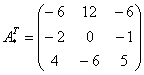 –
транспонированная матрица алгебраических
дополнений.
Обратная матрица:
–
транспонированная матрица алгебраических
дополнений.
Обратная матрица: 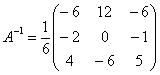 Таким
образом:
Таким
образом:
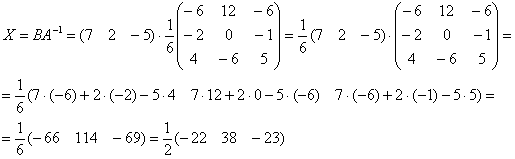 Ответ:
Ответ: ![]() Проверка:
Подставим найденное значение
в
левую часть исходного уравнения:
Проверка:
Подставим найденное значение
в
левую часть исходного уравнения:
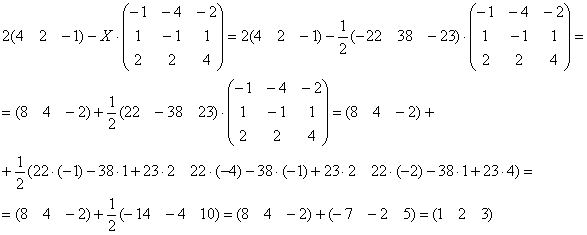 Получена
правая часть исходного уравнения, таким
образом, решение найдено верно.
Получена
правая часть исходного уравнения, таким
образом, решение найдено верно.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
