Матричные выражения

Повторим обычные школьные выражения с числами. Числовое выражение состоит из чисел, знаков математических действий и скобок, например:  . При расчётах справедлив знакомый алгебраический приоритет: сначала учитываются скобки, затем выполняется возведение в степень / извлечение корней, потом умножение / деление и в последнюю очередь – сложение /вычитание.

Если числовое выражение имеет смысл, то результат его вычисления является числом, например:

Матричные выражения устроены практически так же! С тем отличием, что главными действующими лицами выступают матрицы. Плюс некоторые специфические матричные операции, такие, как транспонирование и нахождение обратной матрицы.

Рассмотрим матричное выражение  , где   – некоторые матрицы. В данном матричном выражении три слагаемых и операции сложения/вычитания выполняются в последнюю очередь.

В первом слагаемом   сначала нужно транспонировать матрицу «бэ»:  , потом выполнить умножение   и внести «двойку» в полученную матрицу. Обратите внимание, чтооперация транспонирования имеет более высокий приоритет, чем умножение. Скобки, как и в числовых выражениях, меняют порядок действий:   – тут сначала выполняется умножение  , потом полученная матрица транспонируется и умножается на 2.

Во втором слагаемом   в первую очередь выполняется матричное умножение  , и обратная матрица находится уже от произведения. Если скобки убрать:  , то сначала необходимо найти обратную матрицу  , а затем перемножить матрицы:  .Нахождение обратной матрицы также имеет приоритет перед умножением.

С третьим слагаемым   всё очевидно: возводим матрицу в куб и вносим «пятёрку» в полученную матрицу.

Если матричное выражение имеет смысл, то результат его вычисления является матрицей.

Все задания будут из реальных контрольных работ, и мы начнём с самого простого:

Пример 9

Даны матрицы 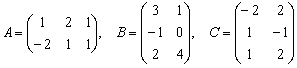 . Найти:

Решение: порядок действий очевиден, сначала выполняется умножение, затем сложение.

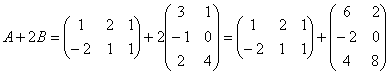Сложение выполнить невозможно, поскольку матрицы разных размеров.

Не удивляйтесь, заведомо невозможные действия часто предлагаются в заданиях данного типа.

Пробуем вычислить второе выражение:

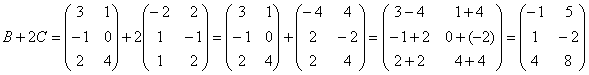
Тут всё нормально.

Ответ: действие   выполнить невозможно,  .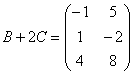

Повысим градус:

Пример 10

Даны матрицы  .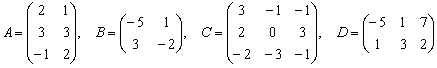

Найти значения выражений: 

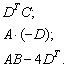
Решение: Разбираемся с произведением  . Сначала транспонируем матрицы «дэ»:

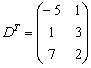
И умножаем матрицы: 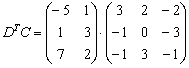Матричное умножение выполнить невозможно, так как число столбцов матрицы   не равно числу строк матрицы  .

А вот с произведением   проблем не возникает:

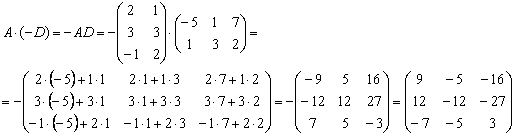
Еще раз заметьте, как на первом же шаге множитель (–1) выносится вперёд, и ноги до него доходят в самую последнюю очередь.

С более сложными выражениями вроде   чайникам рекомендую разбираться поэтапно, чтобы не запутаться:

Сначала находим произведение:

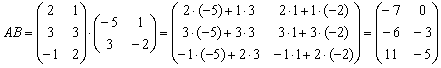
Затем считаем второе слагаемое:

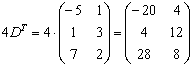
И, наконец, всё выражение:

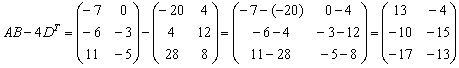
Более подготовленные студенты могут оформить решение одной строкой:

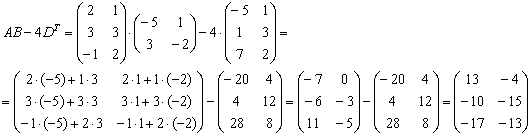
Ответ: действие   выполнить невозможно,   ,  .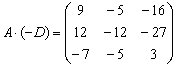

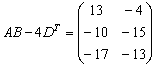Пара заключительных примеров для самостоятельного решения:

Пример 11

Для матриц Примера №10 выполнить действия: 

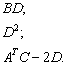
Пример 12

Вычислить значение матричного многочлена  , если  .

В последнем примере решение удобно оформить по пунктам.

Матричные выражения – это просто! И вряд ли на практике вам встретится что-то сложнее, чем разобранные примеры.

Теперь во всеоружии можно приступить к изучению матричных уравнений.

Желаю успехов!

Решения и ответы:

Пример 2: Решение: 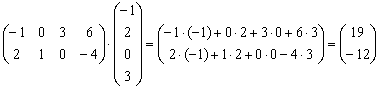Ответ: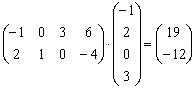 

Пример 5: Решение:  Ответ: 

Пример 7: Решение:  1) Используем формулу  2) Используем формулу  Ответ: 

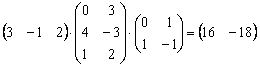
Пример 8: Решение: Сначала возведём матрицу в квадрат: Возведём матрицу в куб: Возведём матрицу в четвёртую степень двумя способами: Ответ: 

Пример 11: Решение:

Возведение в квадрат   невозможно, поскольку операция определена только для квадратных матриц.

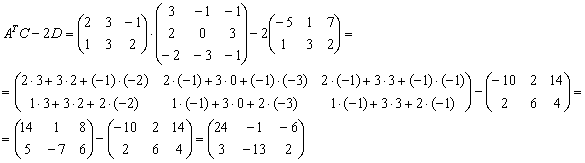
Ответ:  , действие   выполнить невозможно, 

Пример 12: Решение:  1)  2)  3)  4)  5)  Ответ:  Примечание: выражение можно было вычислить и по-другому – предварительно раскрыть скобки: 

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)