5. Початкове ознайомлення учнів з діями додавання та віднімання. Методика вивчення табличних випадків додавання та віднімання одноцифрових чисел.

Теоретичною основою вивчення дії додавання і дії віднімання і розкриття їхнього конкретного смислу є операції об’єднання і різниці (вилучення частини даної множини) множин. Розглядаючи різноманітні предметні множини, діти із двох множин утворюють третю або вилучають частину елементів заданої множини, а потім встановлюють за відомими чисельностями двох множин чисельність новоутворених множин. Як відомо, операція об'єднання двох множин володіє переставною та сполучною властивістю, що створює умови для ознайомлення молодших школярів з відповідними законами додавання.

Існує 3 етапи при розгляді будь-якого питання:

1.Підготовчий. 2.Ознайомлення. 3.Закріплення.

Підготовча робота до ознайомлення дітей з діями додавання і віднімання розпочинається з перших уроків математики в першому класі та завершується з введенням відповідної дії. Мета цього етапу полягає у створенні відповідного підґрунтя для успішного усвідомлення конкретного смислу цих дій та оволодіння відповідними знаннями, уміннями і навичками, тобто в актуалізації опорних знань. Для досягнення поставлених завдань повинна використовуватися, як свідчить аналіз підручників і методичних посібників, така система вправ: 1) практичні вправи на об’єднання предметних множин і на вилучення частини з даної множини з наступним визначенням чисельності утвореної нової множини (використання наочності при виконанні цих вправ дозволяє дітям побачити як чисельність даних множин, так і чисельність новоутвореної множини); 2) вправи, пов’язані з лічбою предметів скінченних множин; 3) вправи на встановлення відповідності між числом і відповідною кількістю предметів, між кількістю предметів і відповідним числом; 4) вправи на визначення попереднього і наступного числа; 5) вправи на запис результатів предметних дій з наочністю з наступним виставленням відповідних карток на набірному полотні; 6) розв’язування задач на збільшення або зменшення числа на кілька одиниць, для практичної ілюстрації яких використовується відповідна предметна чи умовна наочність.

При ознайомленні дітей з діями додавання і віднімання виділяють наступні етапи:

1. Знаходження суми(різниці) двох предметних множин перелічуванням предметів

2. Початкове ознайомлення з діями додавання і віднімання, їх символікою та термінологією, зв’язком між ними.

3. Додавання і віднімання в межах числа, що розглядаються і які виконуються на предметній основі, чи на основі знання складу чисел.

4. Складання і заучування напам’ять таблиць додавання і віднімання в межах 10 з наступним застосуванням цих знань для обчислення значень числових виразів на 2 дії.

5. Ознайомлення з прийомами додавання і віднімання частинами (групами) та переставною властивістю додавання.

Початкове ознайомлення з дією додавання відбувається перед вивченням чисел 6-10, а з дією віднімання – після вивчення числа 10. Такий розрив створено для того, щоб усунути зайві труднощі та полегшити дітям засвоєння відповідних термінів і символів.

Теоретичною основою дії додавання – об’єднання двох скінчених множин, які не мають спільних елементів та знаходження чисельності утвореної множини, якщо відомо чисельність двох перших множин. Наприклад: було 3 білих зірочки і 2 жовтих. Скільки всього зірочок?

В математиці можна записати це прикладом: 3+2 =5.

Способи читання прикладу:

1. До трьох додати два буде п’ять (до числа три додати число два дорівнює п’ять) – за назвою дії.

2. Три плюс два дорівнює п’ять – за назвою знака.

3. Перший доданок - три, другий доданок - два, сума - п’ять – за назвою компонентів дії.

4. Сума чисел три і два дорівнює п’ять – за назвою виразу.

5. Три збільшити на два дорівнює п’ять – за зміною кількості.

Через декілька уроків ознайомлення із дією віднімання. Підготовча робота є аналогічною до додавання.

Теоретичною основою дії віднімання є знаходження потужності різниці двох множин , якщо друга є підмножиною першої.

При ознайомлення з дією віднімання використовують різнорідні множини.

6- 4 = 2 6 - 2 = 4

Однорідні множини

7 – 3 = 4

6- 4 = 2

Способи читання

1. Від шести відняти чотири дорівнює два - за назвою дії.

2. Шість мінус чотири дорівнює два – за назвою знака.

3. Зменшуване - шість, від’ємник - чотири, різниця - два - за назвою компонентів дії.

4. Різниця чисел шість і чотири дорівнює два – за назвою виразу.

5. Шість зменшити на чотири дорівнює два – за зміною кількості.

Формування уявлень про дії додавання та віднімання відбуваються при розгляді таких вправ: 1)розгляд та вивчення напам’ять випадків додавання, пов’язаних з утворенням чисел, наприклад: 5+1, 6+1 тощо; 2) на розкладання чисел на суму двох доданків та на читання прикладів, наприклад: п’ять дорівнює 3 плюс 2, п’ять – це 3 і 2, п’ять складається з 3 і 2 ; 3) на читання прикладів різними відомими на даний час способами; 4) на списування, обчислення та читання прикладів з дошки чи підручника.

Існує взаємозв’язок між дією додавання і віднімання.

Покажемо це на прикладі розгляду такого малюнка (див. малюнок 1).

        

Запропонувавши дітям розглянути малюнок, запитуємо їх: що зображено на малюнку? – квадрати. Які квадрати зображено на малюнку? – білі і чорні. Скільки білих квадратів? – 7. Скільки чорних ? – 2. Скільки всього квадратів? – 9. Якою дією можна знайти їхню кількість? – додавання. Який приклад можна скласти за цим малюнком? – 7+2=9. Прочитайте його різними способами. Чому дорівнює перший доданок? Другий доданок? Сума? Яку дію ми виконаємо, якщо заберемо білі квадрати? – віднімання. Складіть відповідний приклад: 9-7=2. Що позначало у першому прикладі число 9? – суму. Число 7? – перший доданок. Як знайти другий доданок суми? – від суми відняти перший доданок. Отже, якщо від суми відняти один доданок, то одержимо другий доданок. Аналогічна робота проводиться з випадком 9-2=7, а потім вчитель запитує: скільки прикладів на додавання ми мали? – один. Скільки прикладів на віднімання можна скласти з прикладу на додавання? – два. Як знайти перший доданок? Другий доданок? Після цього вчитель, підсумовуючи проведену роботу, формулює загальний висновок: з одного прикладу на додавання можна скласти два приклади на віднімання, якщо від суми відняти один з доданків, то одержимо інший доданок. Відповідно до усвідомлення учнями цього висновку та відповідно до їхніх індивідуальних особливостей поступово переходимо до розв'язування таких завдань без використання наочності.

7+2=9

9-7=2

9-2=7

До табличних випадків додавання відносять додавання одноцифрових чисел 1 + 1 …9 + 9.

Таблиця віднімання – це всі випадки віднімання, які одержують із таблиці додавання.

Табличні випадки додавання і віднімання лежать в основі більшості усних і письмових прийомів обчислень. Без їх знання напам’ять учні відчувають значні труднощі при обчислені. Вчитель повинен забезпечити вивчення таблиць додавання і віднімання напам’ять всіма учнями.

Нині діючою програмою з математики для початкових класів передбачено два етапи вивчення табличних випадків додавання і віднімання. На першому з них складаються і заучуються напам’ять таблиці додавання і віднімання у межах десяти, а на другому – таблиці додавання і віднімання з переходом через десяток. Існують різні підходи методистів до побудови таблиць додавання. Частина методистів стверджує, що всі таблиці додавання потрібно будувати зі сталим другим доданком. Інші методисти вважають, що таблиці додавання потрібно будувати зі сталим першим доданком. У наступній таблиці (див. таблицю № 1) перший підхід представлено у правому стовпці, а другий – у лівому. Кожен із цих підходів має свої позитивні і негативні риси, але відсутні експериментальні дослідження, які б довели абсолютну перевагу того чи іншого способу. Саме тому вчитель вправі використовувати будь-який з цих підходів, але головним завданням вчителя залишається досягнення знання напам’ять цих випадків всіма учнями. Таблиця № 1.

1+2= 3 2+2= 4 3+2= 5 4+2= 6 5+2= 7 6+2= 8 7+2= 9 8+2=10 9+2=11

2+1= 2 2+2= 4 2+3= 5 2+4= 6 2+5= 7 2+6= 8 2+7= 9 2+8=10 2+9=11

Підготовчою роботою до розгляду табличних випадків додавання та віднімання є актуалізація опорних знань, повторення уявлення дітей про конкретний зміст дії додавання і віднімання, зв’язок між цими діями; залежність між компонентами та результатом тощо)

Ознайомлення дітей зі всіма таблицями додавання і віднімання відбувається аналогічно, але кожна наступна таблиця повинна будуватися з більшою часткою самостійності дітей. Разом з тим, кожна нова таблиця повинна з’явитися на очах у дітей.

Наприклад. Таблиця додавання числа 3

• які геометричні фігури зображено на малюнку? (квадрати)

• якого кольору? (білі та блакитні)

• скільки білих квадратиків в першому рядочку? (1)

• поставте у себе на набірному полотні стільки ж квадратиків.

• скільки блакитних квадратиків у 1 рядочку? (3)

• поставте у себе на набірному полотні стільки ж квадратиків

• скільки всього геометричних фігур в 1 рядочку? (4)

• як це записати прикладом?

Аналогічно розглядаємо і 2 + 3… 7 + 3. Перед учнями повинен бути малюнок приблизно такого змісту, як це представлено у наступній таблиці № 2.

1+3= 4 2+3= 5 3+3=  4+3=  5+3= 6+3=  7+3=

      

4-3=1 5-3= 6-3= 7-3= 8-3= 9-3= 10-3=

Відмінність випадків наступних таблиць полягає лише у ступені самостійності дітей при розгляді кожного наступного випадку. Побудувавши таблицю додавання числа 3, запитуємо у дітей що ми побудували?

Щоб побудувати таблицю віднімання числа 3, пропонуємо із кожного прикладу на додавання скласти приклад на віднімання числа 3.

При побудові таблиць додавання числа 2, 3, 4 використовують додавання по 1. Такий прийом більш громісткий, коли доданки - більші числа.

Прийом додавання групами використовують при додаванні більших чисел, що ґрунтується на раніше засвоєних випадків.

3+4 3+4 3+4 3+4

/\ //\\ /\ /\

2+2 1+1+1+1 1+3 3+1

При відніманні теж використовують прийом віднімання групами в межах 5. При поясненні випадків віднімання 6,7,8,9 (без переходу через розряд) використовується прийом, що ґрунтується на зв’язку дії віднімання з дією додавання та знанні складу чисел з двох менших

10-7=3 9-6=3

10=7+3 9=6+3

10-7=3 9-6=3

Щоб діти засвоїли таблиці напам’ять використовуються наступні вправи:

1. На складання таблиці та записування їх у зошит.

2. На читання таблиць (від найбільшого результату до найменшого і навпаки)

3. На відтворення таблиці напам’ять (всієї таблиці в різнобій, з будь – якого місця; робота в парах тощо).

4. Розв’язання прикладів на додавання і віднімання.

5. Розв’язання прикладів , де проміжний результат дитина тримає в пам’яті.

6. Творча робота над таблицями:

- що можна сказати про другі доданки в таблиці? (однакові)

- як змінюються перші доданки? (кожний наступний збільшується на 1)

- як змінюється сума( різниця)?

- чому збільшується сума (різниця)?

7. На розв'язування завдань виду (див. малюнок № 2).

1

2

3

4

5

6

7

+

3

6

7

8

9

-

5

Таблиці з переходом через розряд.

Підготовчим етапом для вивчення таблиці із переходом через розряд є повторення таблиці додавання віднімання без переходу через розряд, складу числа 10з двох доданків. Оскільки теоретичною основою розгляду табличних випадків додавання і віднімання з переходом через десяток є сполучна властивість дії додавання, то слід ввести таке правило на конкретному прикладі: щоб виконати додавання, слід другий доданок розкласти на два числа, перше з яких доповнювало б перший доданок до 10.

Форма пояснення – або стовпцеві:

8 + 3=

2+1

8+2=10

10+1=11

8+3=11

Форма пояснення – або в рядочок:

8 + 3 = 8 +(2 + 1) = 8 + 2+1 =10 + 1 = 11

Під час складання таблиці на віднімання, використовують 3 прийоми обчислень:

1. Віднімання чисел частинами (послідовне віднімання), теоретичною основою є правило віднімання суми від числа, наприклад:

15 – 8=15-(5+3)=15-5-3=7

Щоб відняти два числа, треба від’ємник замінити сумою таких зручних доданків, щоб перший з них дорівнював числу одиниць зменшуваного, після цього віднімаємо числа частинами.

2. Віднімання числа від 10 з наступним додаванням одиниць зменшуваного, теоретичною основою є правило віднімання числа від суми.

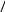
1 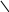5 – 8=

10+5

10 – 8 = 2

2 + 5 =7

15-8=7

Щоб відняти два числа, потрібно зменшуване розкласти на суму розрядних доданків. Від 10 відняти від’ємник і додати кількість одиниць зменшуваного.

3. Знаходження результату віднімання на основі таблиці додавання, теоретичною основою є зв’язок дії додавання і віднімання)

1 5 – 8= Міркування: потрібно від 10 відняти 8. 15 – це 8+7. Якщо від 15 відняти 8, то залишиться 7.

Ці різні прийоми вводяться після ознайомлення з табл. віднімання числа 4.