Вопрос 31

§4 Магнитное поле соленоида и тороида

 

С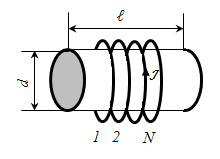 оленоид представляет цилиндрический каркас, на который намотаны витки проволоки. Рассмотрим бесконечно длинный соленоид, т.е. соленоид у которого ? >> d, где ? - длина, d – диаметр соленоида. Внутри такого соленоида магнитное поле однородно. Однороднымназывается поле, силовые линии которого параллельны и густота их постоянна.

 

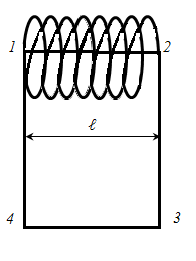
Применим закон полного тока для вычисления напряженности магнитного поля соленоида. Представим контур L, по которому рассматривается циркуляция вектора  , состоящим из четырех связанных участков 1-2; 2-3; 3-4; 4-1. Тогда циркуляция вектора   по выбранному нами контуру L будет равна

.

;

, т.к.    и, следовательно,  ,

, т.к.  мы выбрали участок 3-4 достаточно далеко от соленоида и можно считать, что поле вдали от соленоида равно нулю,

, т.к.    и, следовательно,  .

L охватываетN токов, где N – число витков соленоида, тогда по закону полного тока

 ;

 - магнитное поле бесконечно длинного соленоида

n – плотность намотки – число витков на единицу длины  .

Напряженность поля внутри соленоида равна числу витков, приходящихся на единицу длины соленоида, умноженному на силу тока.

Тороид – тор, с намотанными на него витками проволоки. В отличие от соленоида, у которого магнитное поле имеется как внутри, так и снаружи, у тороида магнитное поле полностью сосредоточено внутри витков, т.е. нет рассеивания энергии магнитного поля.

,

где  .

 – магнитное поле тороида.

Если R >>R_витка, то R ≈r и H = n?.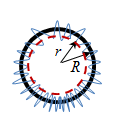

Вопрос 32

 

Если по проводнику течет ток, то вокруг проводника создаётся МП. Мы пока рассматривали провода, по которым текли токи, находящиеся в вакууме. Если провода, несущие ток, находятся в некоторой среде, то м.п. изменяется. Это объясняется тем, что под действием м.п. всякое вещество способно приобретать магнитный момент, или намагничиваться (вещество становится магнетиком).

Вещества, намагничивающиеся во внешнем м.п. против направления поля называются диамагнетиками.

Вещества, слабо намагничивающиеся во внешнем м.п. по направлению поля называются парамагнетиками

Намагниченное в-во создаёт м.п. –  , это м.п. накладывается на м.п., обусловленное токами –  .

Тогда результирующее поле:

.

(54.1)

Истинное (микроскопическое) поле в магнетике сильно изменяется в пределах межмолекулярных расстояний.   – усреднённое макроскопическое поле.

Для объяснения намагничения тел Ампер предположил, что в молекулах вещества циркулируют круговые микроскопические токи, обусловленные движением электронов в атомах и молекулах. Каждый такой ток обладает магнитным моментом и создаёт в окружающем пространстве м.п.

Если внешнее поле отсутствует, то молекулярные токи ориентированы беспорядочным образом, и обусловленное ими результирующее поле равно 0.

 

Магнитные моменты отдельных молекул в отсутствии внешнего поля ориентированы хаотично. Суммарный магнитный момент тела равен 0.

,

(54.2)

, где S-площадь орбиты.

Под действием поля магнитные моменты ( ) молекул приобретают преимущественную ориентацию в одном направлении, магнетик намагничивается , его суммарный магнитный момент становится отличным от 0. Поля отдельных молекулярных токов не компенсируют друг друга и возникает поле  .

Намагничение магнетика естественно характеризовать магнитным моментом единицы объёма.

Намагниченностью называют векторную величину, равную магнитному моменту единицы объёма магнетика:

,

(54.3)

где   - физически бесконечно малый объём, взятый в окрестности рассматриваемой точки;   - магнитный момент отдельной молекулы.

Суммирование производится по всем молекулам, заключённым в объёме   (вспомним   где,  - поляризованность диэлектрика ,   - дипольный элемент ).

Намагниченность можно представить так:

(54.4)

где   - средний магнитный момент одной молекулы , n - концентрация молекул. Тогда  .

В СИ  .

В дальнейшем для упрощения будем считать, что все молекулы в пределах объёма   имеют одинаковый магнитный момент  . Тогда, если  , то  .

Если во всех точках вещества вектор  одинаков, то говорят, что вещество намагничено однородно.