§2 Вращение рамки в магнитном поле

Я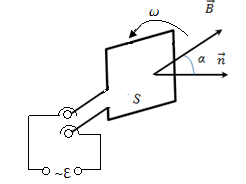 вление электромагнитной индукции используется для преобразования механической энергии и энергии электрического тока в генераторах.

Рамка площадью S вращается в однородном магнитном поле ( )равномерно с постоянной угловой скоростью ω.

α = ωt.

Тогда

При sin ωt=1

и

Т.к. частота сети  , то для увеличения   нужно увеличивать В и S. В можно увеличить, применяя мощные постоянные магниты, или в электромагнитах пропускать большие токи. Сердечник электромагнита выбирают с большим µ. Для увеличения S используют многовитковые обмотки.

Если через рамку, помещенную в магнитном поле, пропускать электрический ток, то на нее будет действовать вращающий момент

и рамка начнет вращаться. На этом принципе основана работа электродвигателей, предназначенных для превращения электрической энергии в механическую.

Вопрос 29

  Возьмем контур l (рис. 2.8), охватывающий прямой ток I, и вычислим для него циркуляцию вектора магнитной индукции   , т.е.   .

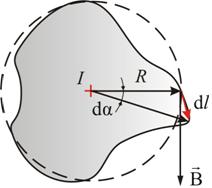
Рис. 2.8

      Вначале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В каждой точке контура вектор    направлен по касательной к окружности, проходящей через эту точку (линии    прямого тока – окружности).

      Воспользуемся свойствами скалярного произведения векторов.

          где    – проекция dl на вектор   ,  но   , где R – расстояние от прямой тока I до dl.

 .

      Отсюда

,

(2.6.1)

      это теорема о циркуляции вектора   :  циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную.

      Иначе обстоит дело, если ток не охватывается контуром (рис. 2.9).

      При обходе радиальная прямая поворачивается сначала в одном направлении (1–2), а потом в другом (2–1). Поэтому   , и следовательно

,

(2.6.2)

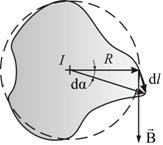
Рис. 2.9

      Итак,      ,  где I – ток, охваченный контуром L.

      Эта формула справедлива и для тока произвольной формы, и для контура произвольной формы.

      Если контур охватывает несколько токов, то

,

(2.6.3)

т.е. циркуляция вектора    равна алгебраической сумме токов, охваченных контуром произвольной формы.

6.3.2. Теорема о циркуляции вектора магнитной индукции

Рассмотрим постоянные токи в вакууме.

 - теорема о циркуляции вектора  :

циркуляция вектора   по произвольному контуру равна произведению   на алгебраическую сумму токов, охватываемых контуром.

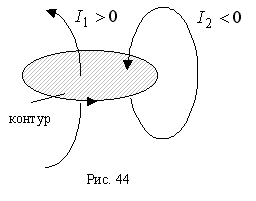
; ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта (рис. 44).

Теорема о циркуляции доказывается посредством закона Био-Савара-Лапласа и подтверждается экспериментально.

Для распределенного по объему тока

,

.

 поле не потенциально (в отличие от электростатического поля); магнитное поле - вихревое (соленоидальное илитрубчатое) поле, свободное от источников (следует из равенства нулю дивергенции).

Соответствующие трубки называются трубками тока; где трубка сжимается, там значение вектора   увеличивается (аналогично изменению скорости течения при изменении проходного сечения; поток во всех сечениях одинаков).

В пределе при 

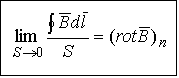 - ротор поля   (вихрь вектора).

Здесь   проекция ротора на направление нормали   к плоскости контура, по которому берется циркуляция.

,

ротор получается в результате векторного перемножения оператора Гамильтона и вектора магнитной индукции ( ).

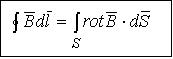- теорема Стокса.

Направление ротора   определяется по направлению нормали  , где  .

.

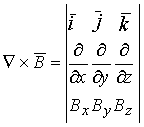 - дифференциальная форма теоремы о циркуляции  .

Для электростатического поля

 поле потенциально   вектор напряженности   можно представить в виде градиента скалярной функции (потенциала  ).

 поле соленоидально   вектор магнитной индукции   можно представить (как и всякий соленоидальный вектор) как вихрь некоторого другого вектора   ( )    ,

где   - векторный потенциал.
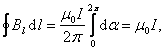