
- •Деление комплексных чисел, формула.
- •Возведение комплексного числа в целую степень
- •§ 6.8. Интеграл типа Коши
- •Определения и понятия теории дифференциальных уравнений.
- •Определение и способ решения
- •Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •Сходимость числовых положительных рядов Необходимый признак сходимости ряда
- •Признак д’Аламбера
- •Признак сходимости д’Аламбера в предельной форме
- •Определение
- •Связанные определения
- •Свойства
- •Формула Тейлора
- •Различные формы остаточного члена
- •Ряды Маклорена некоторых функций
- •Геометрическая вероятность
Определение
Пусть
функция
бесконечно
дифференцируема в некоторой окрестности
точки
![]() .
Формальный ряд
.
Формальный ряд
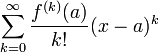
называется
рядом Тейлора функции
![]() в
точке
в
точке
![]() .
.
Связанные определения
В случае, если
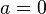 ,
этот ряд также называется рядом
Макло́рена.
,
этот ряд также называется рядом
Макло́рена.
Свойства
Если есть аналитическая функция в любой точке a, то её ряд Тейлора в любой точке области определения сходится к в некоторой окрестности .
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности . Например, Коши предложил такой пример:
![]()
У этой функции все производные в нуле равны нулю, поэтому коэффициенты ряда Тейлора в точке равны нулю.
Формула Тейлора
Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
Теорема:
-
Пусть функция имеет
 производную
в некоторой окрестности
точки
,
производную
в некоторой окрестности
точки
,
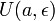
Пусть
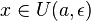
Пусть
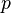 —
произвольное положительное число,
—
произвольное положительное число,
тогда:
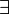 точка
точка
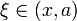 при
при
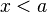 или
или
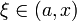 при
при
 :
: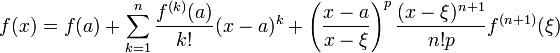
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
Различные формы остаточного члена
В форме Лагранжа:
![]()
В форме Коши:
![]()
В интегральной форме:
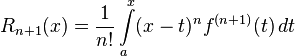
Ослабим предположения:
Пусть функция имеет
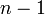 производную
в некоторой окрестности точки
производную
в некоторой окрестности точки
И
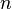 производную
в самой точке
,
тогда:
производную
в самой точке
,
тогда:
![]() —
остаточный член в асимптотической форме
(в форме Пеано,
в локальной форме)
—
остаточный член в асимптотической форме
(в форме Пеано,
в локальной форме)
3.7) Ряд Маклорена
Ряды Маклорена некоторых функций
Экспонента:
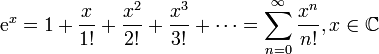
Натуральный логарифм:
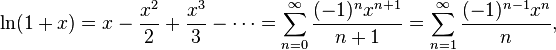 для
всех
для
всех

Биномиальное разложение:
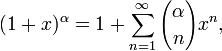 для
всех
и
всех комплексных
для
всех
и
всех комплексных
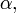 где
где
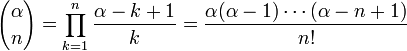
Квадратный корень:
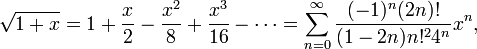 для
всех
для
всех
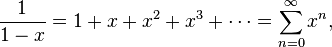 для
всех
для
всех
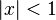
Конечный геометрический ряд:
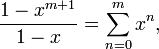 для
всех
для
всех
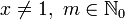
Тригонометрические функции:
Синус:

Косинус:
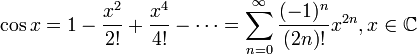
Тангенс:
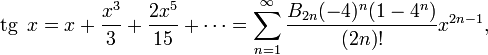 для
всех
для
всех
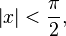 где
где
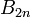 —
Числа
Бернулли
—
Числа
БернуллиСеканс:
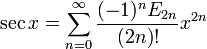 для
всех
для
всех
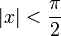 где
где
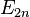 —
числа
Эйлера (англ. Euler
numbers)
—
числа
Эйлера (англ. Euler
numbers)Арксинус:
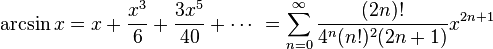 для
всех
для
всех
Арктангенс:
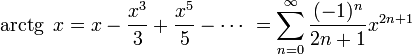 для
всех
для
всех
Гиперболические функции:

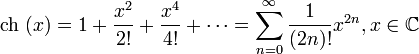
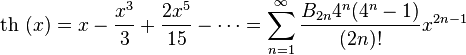 для
всех
для
всех
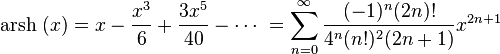 для
всех
для
всех
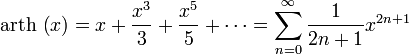 для
всех
для
всех
Геометрическая вероятность
Классическое определение вероятности связано с понятием элементарного события. Рассматривается некий набор Ω равновероятных событий Ai, которые в совокупности дают достоверное событие. И тогда все хорошо: всякое событие разбивается на элементарные, после чего считается его вероятность.
Однако, далеко не всегда исходный набор Ω (т.е. пространство всех элементарных событий) является конечным. Например, в качестве Ω можно взять ограниченное множество точек на плоскости или отрезок на прямой.
В качестве события A можно рассмотреть любую подобласть области Ω. Например, фигуру внутри исходной фигуры на плоскости или отрезок, лежащий внутри исходного отрезка на прямой.
Заметим, что элементарным событием на таком множестве может быть только точка. В самом деле, если множество содержит более одной точки, его можно разбить на два непустых подмножества. Следовательно, такое множество уже неэлементарно.
Теперь определим вероятность. Тут тоже все легко: вероятность «попадания» в каждую конкретную точку равна нулю. Иначе получим бесконечную сумму одинаковых положительных слагаемых (ведь элементарные события равновероятны), которые в сумме по-любому больше P(Ω) = 1.
Итак, элементарные события для бесконечных областей Ω — это отдельные точки, причем вероятность «попадания» в любую из них равна нулю. Но как искать вероятность неэлементарного события, которое, подобно Ω, содержит бесконечное множество точек? Вот мы и пришли к определению геометрической вероятности.
Определение
Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω:
![]()
