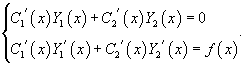Определение и способ решения

Пусть — некоторая функция, — ее производная. Для удобства будем записывать производную виде , имеющем смысл отношения бесконечно малых приращений — дифференциалов. Дифференциал — приращение значения переменной в окрестности , стремящееся к нулю. Дифференциал функции — малое приращение функции, . Пусть и — некоторые функции от и . Рассмотрим уравнение

.

Уравнение такого вида называется обыкновенным дифференциальным уравнением с разделяющимися переменными. Умножим его на :

.

Последнее равенство означает, что малые приращения левой и правой частей равны. Поэтому их суммы также равны. Предположим что при и возьмем интегралы от левой и правой частей. Пределы интегрирования — от до для левой части и от для для правой части уравнения:

.

Решая получившееся в результате интегрирования алгебраическое уравнение, мы можем выразить .

Значения и называются начальными условиями. В случае других начальных условий решение уравнения будет отличаться на постоянную. Поэтому, если начальные условия не даны, можно взять первообразные левой и правой частей и прибавить к ним константу. Используя неопределенный интеграл — обозначение множества первообразных — , где — первообразная , — произвольная постоянная, запишем это в виде

.

Следует отметить, что у дифференциального уравнения с разделяющимися переменными могут существовать так называемые нулевые решения — постоянные , удовлетворяющие уравнению . При них равны нулю как правая, так и левая части дифференциального уравнения (поскольку производная константы равна нулю).

2.3)

(О существовании и единственности решения задачи Коши). Пусть   - непрерывная функция в области , причем   - также непрерывен в . Тогда для любой точки   задача Коши: 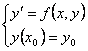 имеет решение, причем единственное в том смысле, что если есть 2 ее решения   и , определенные на интервалах   и , содержащих точку , то они совпадают на пересечении  этих интервалов.

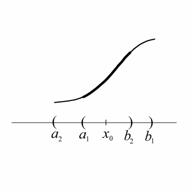
Теорему оставим без доказательства.

Замечание. Говорят, что решение  дифференциального уравнения на интервале  есть продолжение решения   на , если  и  на . Также говорят, что решение   - максимальное или непродолжаемое относительно , если  не обладает продолжениями, целиком лежащими в .

На основании этого замечания можно сказать, что при условиях теоремы существует единственное максимальное (непродолжаемое) решение задачи Коши.

Геометрический смысл сформулированной теоремы состоит в следующем. Левая часть уравнения   представляет собой  - тангенс угла наклона касательной к графику искомой функции в точке , а правая часть  задает его численное значение   в этой точке. Поэтому можно считать, что уравнение задает поле направлений на области , т.е. к каждой точке   прикреплен вектор, указывающий направление касательной к искомой интергальной кривой.

2.3)

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

В этой статье мы разберем принципы решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами , где p и q – произвольные действительные числа. Сначала остановимся на теории, далее применим полученные результаты в решении примеров и задач.

Если Вам будут встречаться незнакомые термины, то обращайтесь к разделу определения и понятия теории дифференциальных уравнений.

Сформулируем теорему, которая указывает, в каком виде находить общее решение ЛОДУ.

Теорема.

Общее решение линейного однородного дифференциального уравнения с непрерывными на интервале интегрирования X коэффициентами определяется линейной комбинацией 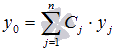, где - линейно независимые частные решения ЛОДУ на X, а - произвольные постоянные.

Таким образом, общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид y₀=C₁⋅y₁+C₂⋅y₂ , где y₁ и y₂ – частные линейно независимые решения, а С₁ и C₂ – произвольные постоянные. Осталось научиться находить частные решения y₁ и y₂.

Эйлер предложил искать частные решения в виде .

Если принять частным решением ЛОДУ второго порядка с постоянными коэффициентами , то при подстановке этого решения в уравнение мы должны получить тождество:

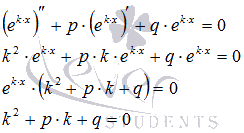
Так мы получили так называемое характеристическое уравнение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами. Решения k₁ и k₂ этого характеристического уравнения определяют частные решения и нашего ЛОДУ второго порядка с постоянными коэффициентами.

В зависимости от коэффициентов p и q корни характеристического уравнения могут быть:

1. действительными и различными ,

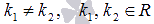2. действительными и совпадающими ,

3. комплексно сопряженной парой .

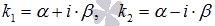В первом случае линейно независимыми частными решениями исходного дифференциального уравнения являются и , общее решение ЛОДУ второго порядка с постоянными коэффициентами есть .

Функции и действительно линейно независимы, так как определитель Вронского 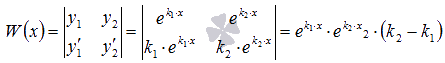отличен от нуля для любых действительных x при .

Во втором случае одним частным решением является функция . В качестве второго частного решения берется . Покажем, что действительно является частным решением ЛОДУ второго порядка с постоянными коэффициентами и докажем линейную независимость y₁ и y₂.

Так как k₁ = k₀ и k₂ = k₀ совпадающие корни характеристического уравнения, то оно имеет вид . Следовательно, - исходное линейное однородное дифференциальное уравнение. Подставим в него и убедимся, что уравнение обращается в тождество:

Таким образом, является частным решением исходного уравнения.

Покажем линейную независимость функций и . Для этого вычислим определитель Вронского и убедимся, что он отличен от нуля.

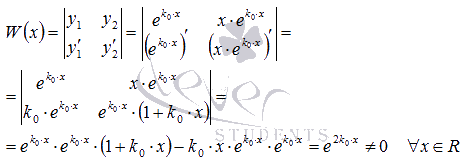
Вывод: линейно независимыми частными решениями ЛОДУ второго порядка с постоянными коэффициентами являются и , и общее решение есть при .

В третьем случае имеем пару комплексных частных решений ЛОДУ и . Общее решение запишется как . Эти частные решения могут быть заменены двумя действительными функциями и , соответствующими действительной и мнимой частям. Это хорошо видно, если преобразовать общее решение , воспользовавшись формулами из теории функции комплексного переменного вида : 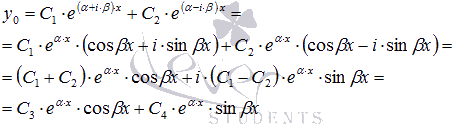где С₃ и С₄ – произвольные постоянные.

Итак, обобщим теорию.

Алгоритм нахождения общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами .

1. Записываем характеристическое уравнение k² + p ⋅ k + q = 0.

2. Находим корни характеристического уравнения k₁ и k₂.

3. В зависимости от значений корней характеристического уравнения записываем общее решение ЛОДУ с постоянными коэффициентами в виде:

   • , если ;

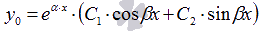   • , если ;

   • , если .

2.4)

Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Структура общего решения Линейное неоднородное уравнение данного типа имеет вид: где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение: Теорема: Общее решение неоднородного уравнения является суммой общего решения y0(x) соответствуюшего однородного уравнения и частного решения y1(x) неоднородного уравнения: Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений. Метод вариации постоянных Если общее решение y0 ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных. Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид: Вместо постоянных C1 и C2 будем рассматривать вспомогательные функции C1(x) и C2(x). Будем искать эти функции такими, чтобы решение удовлетворяло неоднородному уравнению с правой частью f(x). Неизвестные функции C1(x) и C2(x) определяются из системы двух уравнений: Метод неопределенных коэффициентов Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов. Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как где Pn(x) и Qm(x) − многочлены степени n и m, соответственно. В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения. В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель xs, где s − кратность корня α в характеристическом уравнении. В случае 2, если число α + βi совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x. Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение. Принцип суперпозиции Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.

2.5)

Частным решением уравнения (*) называется решение, которое получается из общего решения, если придавать постоянным С₁, С₂, …, С_n определенные числовые значения.

3.1)