1)

Модуль и аргумент

Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).

Модуль комплексного числа обозначается и определяется выражением . Часто обозначается буквами или . Если является вещественным числом, то совпадает с абсолютной величиной этого вещественного числа.

Для любых имеют место следующие свойства модуля. :

1) , причём тогда и только тогда, когда ;;

2) (неравенство треугольника);

3) ;

4) .

Из третьего свойства следует , где . Данное свойство модуля вместе с первыми двумя свойствами вводят на множестве комплексных чисел структуру двумерного нормированного пространства над полем .

5) Для пары комплексных чисел и модуль их разности равен расстоянию между соответствующими точками комплексной плоскости.

Угол (в радианах) радиус-вектора точки, соответствующей числу , называется аргументом числа и обозначается .

• Из этого определения следует, что ; ; .

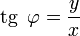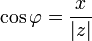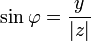• Для комплексного нуля значение аргумента не определено, для ненулевого числа аргумент определяется с точностью до 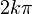, где 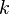 — любое целое число.

• Главным значением аргумента называется такое значение , что 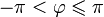. Часто главное значение обозначается ^[4]. Главное значение аргумента обратного числа отличается знаком от аргумента исходного: .

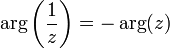3)

Произведением комплексных чисел и называется комплексное число

§

Так же как и в случае вещественных чисел, для знака умножения используют ; часто его вовсе опускают: .

П

Пример. , , .

В отличие от суммы комплексных чисел, определение произведения кажется довольно искусственным. Ответ на вопрос

4)

Деление комплексных чисел, формула.

В соответсвии с определением деления действительных чисел устанавливается следующее опреденеие. Разделить комплексное число a + b·i (делимое) на комплексное число a′ + b′·i (делитель) - значит найти такое число x + y·i (частное), которое, будучи помножено на делитель, даст делимое.

Если делитель не равен нулю, то деление всегда возможно и частное единственно.

Частное комплексных чисел a + b·i, и a′ + b′·i вычисляется по формуле:

1.	a+b·i a′+b′·i = a·a′−b·b′ a′2+b′2 + a′·b−b′·a a′2+b′2 · i

5)

Возведение комплексного числа в целую степень

Пусть дано комплексное число . Для возведения комплексного числа в натуральную степень нужно возвести в эту степень его модуль, а аргумент умножить на показатель степени. Это правило известно в математике как формула Муавра:

6)

.4. Тригонометрическая форма записи комплексного числа.

   Если точка z комплексной плоскости имеет декартовые координаты (х, у), т.е.  и полярные , то они связаны соотношением (1):

                             .

По определению,  и из (1) получаем:

                             .                                   (9)

Подставляя в алгебраическую форму записи числа z получаем: . Или

                                             (10)

Определение. Запись комплексного числа в виде (3) называется его тригонометрической формой.

Замечание. Поскольку одну букву писать экономнее нежели несколько, то чаще всего тригонометрическую форму комплексного числа пишут в виде:

                          ,                                (11)

где .

Теорема. (О равенстве комплексных чисел в тригонометрической форме.)

Два комплексных числа равны тогда и только тогда, когда равны их модули и аргументы.

   Доказательство. Так как между всеми комплексными числами и всеми точками комплексной плоскости существует взаимно однозначное соответствие, то равные комплексные числа отождествляются на комплексной плоскости с одной и той же точкой, следовательно, имеют одни и те же полярные координаты, т.е. полярный радиус, который по определению равен модулю комплексного числа, и полярный угол, который по определению равен аргументу комплексного числа. Обратно, если комплексные числа имеют равные модули и аргументы, то они изображаются на комплексной плоскости одной точкой и, следовательно, равны.

Теорема доказана.

   Используя соотношения, которые связывают полярные и декартовые координаты точки плоскости, можно найти модуль и аргумент комплексного числа зная его действительную и мнимую части.

   Пусть , т.е. , . Тогда

                                    ,                               (12)

, если точка z лежит в первой или четвертой четверти или , если точка z лежит во второй или третьей четверти. Также можно пользоваться формулами (6) – (8) п.1, где .

7)

§ 6.8. Интеграл типа Коши

Выражение

,

где  - аналитическая функция на замкнутой области , ограниченной положительно ориентированным контуром , называется интегралом Коши.

2.1)