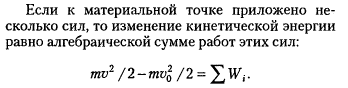14.Теорема о работе силы тяжести. Работа силы, приложенной к вращающемуся телу. Мощность.
Теорема о работе силы тяжести:
Работа силы тяжести не зависит от вида траектории и равна произведению модуля силы на вертикальное перемещение точки её приложения.
А=mgh
Работа силы при вращении тела:
15. Энергетические теоремы динамики материальной точки. Теорема об изменении количества движения.
Вопрос 16.
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ.
1) ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ.
Изменение кинетической энергии механической системы на некотором ее перемещении равно сумме работ внешних и внутренних сил, приложенных к точкам системы, на том же перемещении.
Рассмотрим движение произвольной точки системы из первого положения во второе:
где Fke - внешние силы, действующие на систему,
Fki - внутренние силы системы.
Умножим обе части уравнения скалярно на дифференциал радиуса-вектора drk тогда
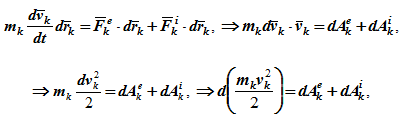
или dTk = dAke + dAki , (1.1)
где Tk - кинетическая энергия точки;
далее получим
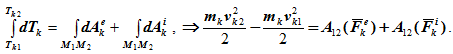
Просуммируем по всем точкам системы
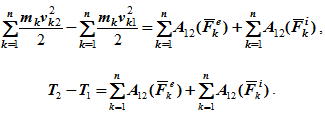
То есть, изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на систему, на том же перемещении.
Если в формуле (1.1) обе части уравнения разделить на dt, то можно записать теорему об изменении кинетической энергии системы в дифференциальной форме: производная по времени от кинетической энергии механической системы равна сумме мощностей внешних и внутренних сил, действующих на систему.
dTk / dt = dAke / dt + dAki / dt , dTk / dt =Nke + Nki.
Суммируя по всем точкам системы, получим
dT / dt = ∑Nke + ∑Nki.
Из теоремы следует закон сохранения механической энергии.
Если механическая система является консервативной, то полная механическая энергия системы Т + П, равная сумме кинетической и потенциальной энергий, при движении системы остается постоянной.
При движении механической системы в потенциальном силовом поле получаем
T2 -T1 = A12.
По определению потенциальной энергии
П1 - П2 = A12.
Тогда
T2 - T1 = П1 - П2 , T2+ П2 = T1 + П1 , Т + П = const.
2) ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ.
сли в замкнутой системе не действуют силы, трения и силы сопротивления, то сумма кинетической и потенциальной энергии всех тел системы остается величиной постоянной.
Рассмотрим пример проявления этого закона. Пусть тело, поднятое над Землей, обладает потенциальной энергией Е1 = mgh1 и скоростью v1направленной вниз. В результате свободного падения тело переместилось в точку с высотой h2 (E2 = mgh2), при этом скорость его возросла от v1 до v2. Следовательно, его кинетическая энергия возросла от
Рассмотрим ограничения, которые были сформулированы в законе сохранения полной механической энергии.
Что же происходит с механической энергией, если в системе действует сила трения?
В реальных процессах, где действуют силы трения, наблюдается отклонение от закона сохранения механической энергии. Например, при падении тела на Землю сначала кинетическая энергия тела возрастает, поскольку увеличивается скорость. Возрастает и сила сопротивления, которая увеличивается с возрастанием скорости. Со временем она будет компенсировать силу тяжести, и в дальнейшем при уменьшении потенциальной энергии относительно Земли кинетическая энергия не возрастает.
Это явление выходит за рамки механики, поскольку работа сил сопротивления приводит к изменению температуры тела. Нагревание тел при действии трения легко обнаружить, потерев ладони друг о друга.
Изменение тепловой (или внутренней) энергии возникает в результате работы сил трения или сопротивления. Оно равно изменению механической энергии. Таким образом, сумма полной энергии тел при взаимодействии есть величина постоянная (с учетом преобразования механической энергии во внутреннюю).
Энергия измеряется в тех же единицах, что и работа. В итоге отметим, что изменить механическую энергию можно только одним способом - совершить работу
17) Динамика системы материальных точек.
Системой материальных точек или механической системы, называют систему взаимных между собой материальных точек. Твёрдое тело в механике рассматривается как совокупность материальных точек. Различают свободные и несвободные системы. Свободной, называется система точек, которые могут получить произвольное перемещение и скорости, в противном случае несвободная система.
Силы, действующие на систему.
С одной стороны силы, действующие на систему, различаются на активные и пассивные, другой стороны – внешние и внутренние.
1) Геометрическая сумма внутренних сил равна нулю. Рассмотрим систему, состоящую их трёх точек. Согласно закону действия и противодействия, каждой внутренней силе соответствует сила, равная по величине, но противоположная по направлению. Из этих формул видно, что величина динамических деформаций, напряжений и усилий зависит от величины статической деформации, т. е. от жесткости и продольных размеров ударяемого тела; ниже это дополнительно будет показано на отдельных примерах.
2
)
Геометрическая сумма моментов всех
внутренних сил системы относительно
любой точек нулю.
|
(3.12) |
Таким
образом, центр инерции механической
системы движется как материальная
точка, масса которой равна массе всей
системы и на которую действует сила,
равная главному вектору внешних сил,
приложенных к системе. В общем случае
движение твердого тела можно рассматривать
как сумму двух движений: поступательного
со скоростью 
,
равной скорости 
центра
инерции тела, и вращения вокруг центра
инерции. Поэтому последнее уравнение
часто называют основным уравнением
динамики поступательного движения
твердого тела.
Уравнение
динамики твердого тела,
вращающегося вокруг неподвижной
оси:
суммарный момент сил, действующих
на тело, равен произведению момента
инерции тела на угловое ускорение:
.
Учитывая,
что момент импульса твердого тела 
,
уравнение динамики твердого тела можно
представить в виде
.Под
моментом инерции твердого
тела относительно оси
понимается сумма произведений
масс точек тела на квадраты расстояний этих точек до рассматриваемой оси
Теорема Гюйгенса — Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
,
где 
—
полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
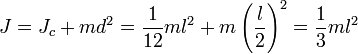
В18)
Сравнение формул динамики для поступательного и вращательного движений твердого тела.
19) Количество движения системы материальных точек. Кинетический момент.
Теорема об изменении кинетического момента материальной точки и системы точек.
