1)
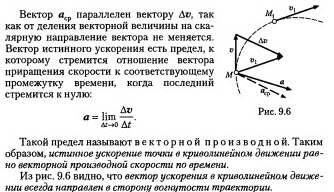
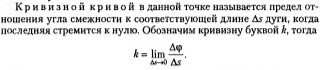
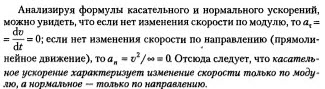
2. Частные случаи движения точки: равномерное прямолинейное, равномерное криволинейное, равнопеременное движение. Классификация видов механического движения.
Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу).
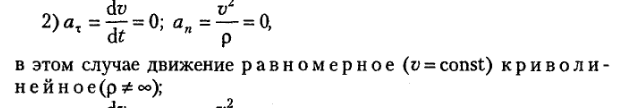
Равнопеременное движение — движение с постоянным ускорением.
Механическое движение можно рассматривать для разных механических объектов:
Движение материальной точки полностью определяется изменением её координат во времени (например, двух на плоскости). Изучением этого занимается кинематика точки. В частности, важными характеристиками движения являются траектория материальной точки, перемещение, скорость и ускорение.
Прямолинейное движение точки (когда она всегда находится на прямой, скорость параллельна этой прямой)
Криволинейное движение — движение точки по траектории, не представляющей собою прямую, с произвольным ускорением и произвольной скоростью в любой момент времени (например, движение по окружности).
Движение твёрдого тела складывается из движения какой-либо его точки (например, центра масс) и вращательного движения вокруг этой точки. Изучается кинематикой твёрдого тела.
Если вращение отсутствует, то движение называется поступательным и полностью определяется движением выбранной точки.
Для описания вращательного движения — движения тела относительно выбранной точки, например закреплённого в точке, — используют Углы Эйлера.
Также для твёрдого тела выделяют плоское движение — движение, при котором траектории всех точек лежат в параллельных плоскостях, при этом оно полностью определяется одним из сечений тела, а сечение тела — положением любых двух точек.
Движение сплошной среды. Здесь предполагается, что движение отдельных частиц среды довольно независимо друг от друга (обычно ограничено лишь условиями непрерывности полей скорости), поэтому число определяющих координат бесконечно (неизвестными становятся функции).
4)Сложное движение точки. Сложение ускорений. Теорема Кориолиса.
Теорема о сложении ускорений (теорема Кориолиса).
При непоступательном переносном движении абсолютное ускорение точки находится как сумма трех ускорений: относительного, переносного и кориолисова ускорений.
,
,
где 
−
угловая скорость переносного
вращения. (Далее 
)
Ускорение Кориолиса
Ускорение Кориолиса учитывает изменение относительной скорости, вызванное переносным движением, и изменение переносной скорости, вызванное относительным движением.
Способы вычисления ускорения Кориолиса:
1. По правилу векторного произведения
.
2.По правилу Жуковского
|
|
|
|
Для
определения направления ускорения
Кориолиса надо вектор относительной
скорости (рис.4) спроецировать на
плоскость, перпендикулярную оси вращения,
и повернуть в сторону вращения на угол 
.
Сложное движение точки :
5. Плоскопараллельное движение твердого тела. Основные понятия и определения. Метод мгновенных центров скоростей (м.Ц.С.) Свойства м.Ц.С.
Вопрос 6.
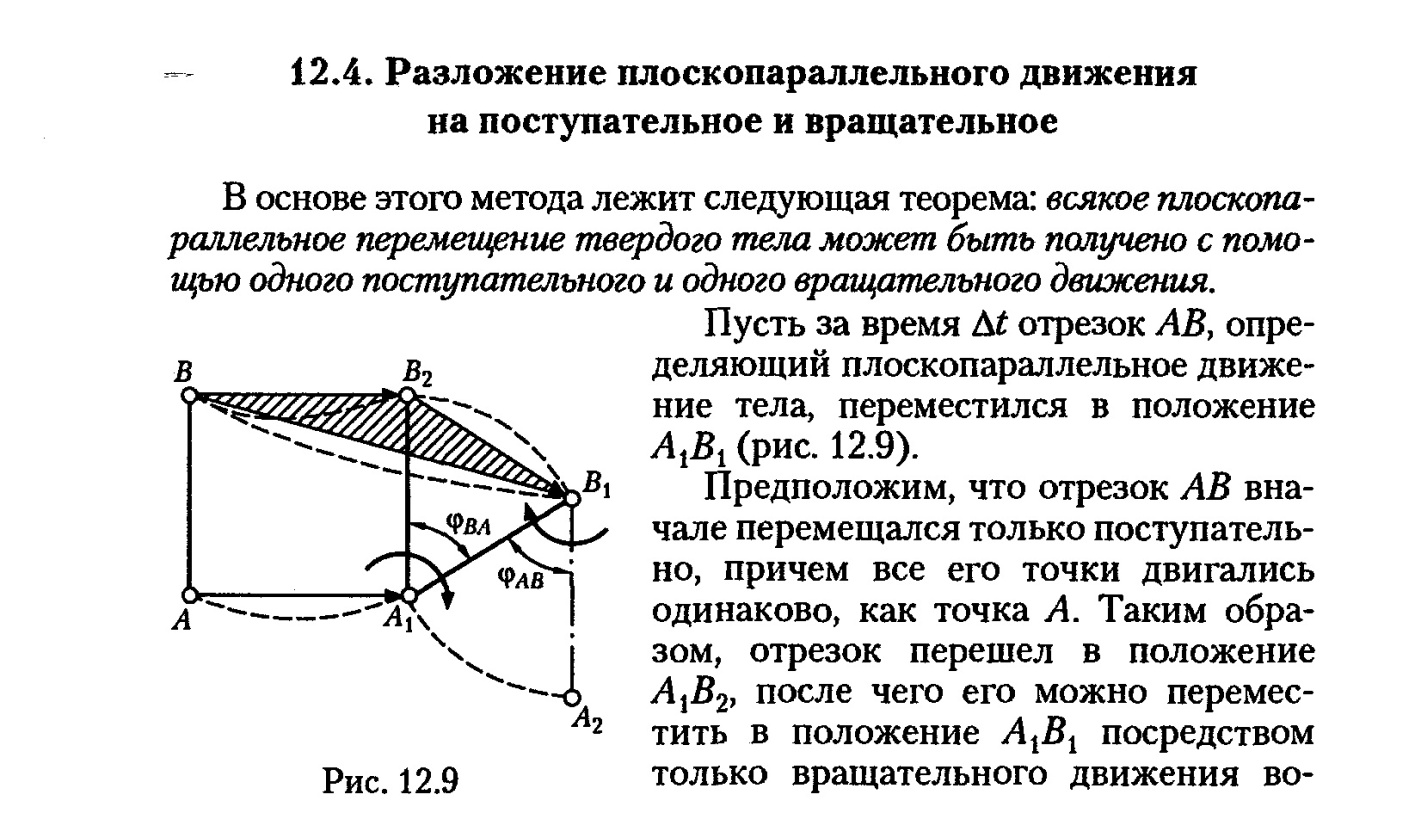
РАЗЛОЖЕНИЕ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ.ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ 2-Х ТОЧЕК ТЕЛА ПРИ ПЛОСКОМ ДВИЖЕНИИ.
ПЛОСКОПАРАЛЛЕ́ЛЬНОЕ ДВИЖЕ́НИЕ (плоское движение) — вид движения абсолютно твёрдого тела, при котором траектории всех точек тела располагаются в плоскостях, параллельных заданной плоскости.
Примером плоскопараллельного движения по отношению к вертикальной плоскости, относительно которой тело движется в параллельном направлении, является качение колеса по горизонтальной дороге.
В основе лежит теорема:
Любое плоскопараллельное перемещение
твердого тела может быть получено с
помощью одного поступательного и одного
вращательного движения.
7) Сферическое движение твердого тела.
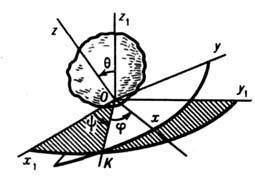
Сф.движ – движение твердого тела, одна из точек которого во все время движения остается неподвижной (напр. движение волчка). Точки тела движутся по сферическим поверхностям. Положение тела определяют при помощи трех углов. Для этого задаются две системы координат: неподвижная Оxyz и подвижная О, связанная с твердым телом. Линия ОJ – линия узлов, задаются углы: – угол прецессии, – угол нутации, – угол собственного вращения — углы Эйлера. Таким образом уравнения сферического движения:=f1(t); =f2(t); =f3(t). Углы отсчитываются от осей против хода час.стр.
Движение свободного тв.тела (общий случай движения). Свободное тв.тело имеет шесть степеней свободы. При рассмотрении движения св.тв.тела, кроме неподвижной системы координат Oxyz, вводится подвижная система координат Ax1y1z1, которая связана с телом в точке А. Тогда движ. св.тв.тела представляет собой сложное движение, которое можно рассматривать как состоящее из поступательного движения вместе с полюсом (А) и сферич. движ. вокруг полюса. Ур-ия движ.св.тв.тела: xA=f1(t); yA=f2(t); zA=f3(t); =f4(t);=f5(t); =f6(t) (углы Эйлера). Первые три ур-ия определяют поступательную часть движ. и зависят от выбора полюса, остальные три определяют сферич. движ. вокруг полюса и от выбора полюса не зависят. Скорость любой точки св.тв.тела = геометрической сумме скорости полюса и скорости этой точки в ее сферическом движении вокруг полюса.
Ускорение точки св.тв.тела = геометрической сумме ускорения полюса, осестремительного ускорения точки и ее вращательного ускорения, определенных относительно мгновенной оси и оси углового ускорения, проходящих через полюс.
ЭЙЛЕРА УГЛЫ
-
три угла 
определяющие
положение твёрдого тела, имеющего
неподвижную точку О (напр., гироскопа), по
отношению к неподвижным прямоуг. осям 
.
Если с телом жёстко связать прямоуг.
оси 
(рис.)
и обозначить линию пересечения
плоскостей 
и Оху через OK (линия
узлов), то Э. у. будут: угол собственного
вращения 
(угол
поворота вокруг оси Oz), угол
прецессии 
(угол
поворота вокруг оси Oz1)
и угол нутации 
(угол
поворота вокруг линии узлов OK); положит,
направления отсчёта углов показаны на
рисунке дуговыми стрелками. Положение
тела будет определяться однозначно,
если считать углы 
изменяющимися
от 0 до 
а
угол q - от 0 до 
Э.
у. широко пользуются в динамике твёрдого
тела, в частности в теории гироскопа и
в небесной механике.
8)
