10 Поляризация

Диэлектрик, помещенный во внешнее электрическое поле, поляризуется под действием этого поля. Поляризацией диэлектрика называется процесс приобретения им отличного от нуля макроскопического дипольного момента. Степень поляризации диэлектрика характеризуется векторной величиной, которая называется поляризованостью или вектором поляризации (P). Поляризованность определяется как электрический момент единицы объема диэлектрика

,

где N - число молекул в объеме  . В диэлектриках различают следующие типы поляризации: электронную, ориентационную и решеточную (для ионных кристаллов). Электронный тип поляризации характерен для диэлектриков с неполярными молекулами. Во внешнем электрическом поле (рис. 2.1) положительные заряды внутри молекулы смещаются по направлению поля, а отрицательные в противоположном направлении, в результате чего молекулы приобретают дипольный момент, направленный вдоль внешнего поля 

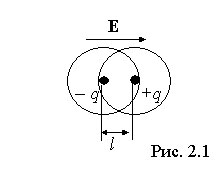
Индуцированный дипольный момент молекулы пропорционален напряженности внешнего электрического поля  , где   - поляризуемость молекулы. Значение поляризованности в этом случае равно  , где n - концентрация молекул  ;   - индуцированный дипольный момент молекулы, который одинаков для всех молекул и направление которого совпадает с направлением внешнего поля. Ориентационнный тип поляризации характерен для полярных диэлектриков. В отсутствие внешнего электрического поля молекулярные диполи ориентированы случайным образом, так что макроскопический электрический момент диэлектрика равен нулю.

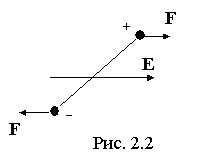
Если поместить такой диэлектрик во внешнее электрическое поле, то на молекулу-диполь будет действовать момент сил (рис. 2.2), стремящийся ориентировать ее дипольный момент в направлении напряженности поля. Однако полной ориентации не происходит, поскольку тепловое движение стремится разрушить действие внешнего электрического поля. Такая поляризация называется ориентационной. Поляризованность в этом случае равна  , где <p> - среднее значение составляющей дипольного момента молекулы в направлении внешнего поля. 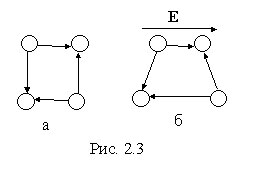Решеточный тип поляризации характерен для ионных кристаллов. В ионных кристаллах (NaCl и т.д.) в отсутствие внешнего поля дипольный момент каждой элементарной ячейки равен нулю (рис. 2.3.а), под влиянием внешнего электрического поля положительные и отрицательные ионы смещаются в противоположные стороны (рис. 2.3.б). Каждая ячейка кристалла становится диполем, кристалл поляризуется. Такая поляризация называется решеточной. Поляризованность и в этом случае можно определить как  , где  - значение дипольного момента элементарной ячейки, n - число ячеек в единице объема. 

11

Связанные заряды. В результате процесса поляризации в объеме (или на поверхности) диэлектрика возникают нескомпенсированные заряды, которые называются поляризационными, или связанными. Частицы, обладающие этими зарядами, входят в состав молекул и под действием внешнего электрического поля смещаются из своих положений равновесия, не покидая молекулы, в состав которой они входят. Связанные заряды характеризуют поверхностной плотностью  . 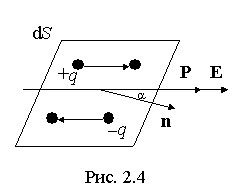Выделим в поляризованном диэлектрике наклонную призму с основанием S и ребром L, параллельным вектору поляризации P (рис. 2.4). В результате поляризации на одном из оснований призмы появятся отрицательные заряды с поверхностной плотностью  , а на другой положительные заряды с плотностью  . С макроскопической точки зрения, рассматриваемый объем эквивалентен диполю, образованному зарядами   и  , которые отстоят друг от друга на расстояние L, тогда электрический момент призмы равен  . С другой стороны, электрический момент единицы объема равен  , где  - угол, между направлением нормали к основанию призмы и вектором P. Произведение   есть объем призмы. Приравняв друг к другу оба выражения для электрического момента, получаем, что поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации:

,

где n - единичный вектор нормали к поверхности диэлектрика.

Если вектор поляризации P различен в разных точках объема диэлектрика, то в диэлектрике возникают объемные поляризационные заряды, объемная плотность которых  .

12

Электрическое смещение. Теорема Гаусса для электростатического поля в диэлектрике

 Из предыдущего раздела следует, что напряженность поля Е при переходе из вакуума в диэлектрик изменяется скачкообразно. Такой же эффект будет наблюдаться при переходе из одного диэлектрика в другой. Скачкообразное изменение вектора  , обусловленное его зависимостью от e, затрудняет расчет полей при решении ряда задач. Поэтому для характеристики электрического поля целесообразно внести векторную величину  , которая не зависела бы от e. Этот вектор  , он называется вектором электрического смещения или электрической индукции. Подставим в последнее соотношение e = 1+æ и получим

.

 Обратимся вновь к рисунку 1.19. Внешнее поле   создается свободными зарядами заряженных поверхностей. Внутри диэлектрика действует также поле связанных зарядов, т.е. зарядов, входящих в состав атомов и молекул диэлектрика. Заряды, не связанные с перечисленными выше частицами диэлектрика, называют свободными. Это: а) заряды частиц, способных перемещаться под действием электрического поля на макроскопические расстояния (электронов проводимости в металлах, электронов в вакууме, ионов в электролитах и т.п.); б) положительные заряды атомных остатков в металлах; в) избыточные заряды, сообщенные телу и нарушающие его электрическую нейтральность (например, заряды, нанесенные извне на поверхность диэлектрика).

 Электрическое поле в диэлектрической среде создается как свободными, так и связанными зарядами. Первичным источником поля являются свободные заряды, а поле связанных зарядов возникает в результате поляризации диэлектрика при помещении его в поле свободных зарядов. Причем, поле связанных зарядов может вызвать перераспределение свободных зарядов и изменить поле этих зарядов.

 Поэтому вектор   характеризует электростатическое поле, создаваемое свободными зарядами в вакууме (e=1), но при таком их распределении в пространстве, какое будет при наличии диэлектрика. Линии вектора   начинаются и заканчиваются на любых зарядах - свободных и связанных, а линии вектора   - только на свободных зарядах и они проходят диэлектрик не прерываясь. Смысл введения вектора электрического смещения состоит в том, что поток вектора   через любую замкнутую поверхность определяется только свободными зарядами, а не всеми зарядами, находящимися внутри объема, ограничивающего данную поверхность S (как это было с потоком  ). Это позволяет не рассматривать связанные (поляризованные) заряды и упрощает решение многих задач.

 Поток вектора   через произвольную замкнутую поверхность S равен 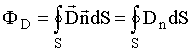 , где Dn - проекция вектора    на нормаль   к площадке dS. Теорема Гаусса для электростатического поля в диэлектрике выводится аналогично выводу теоремы для вакуума, в результате получаем 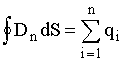 , где в правой части сумма свободных зарядов.

13

Исследуем связь между векторами Е и D на границе раздела двух однородных изотропных диэлектриков (у которых диэлектрические проницаемости равны ε₁ и ε₂) при отсутствии на границе свободных зарядов. 

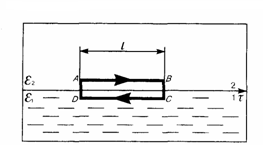
Рис.1

Проведем вблизи границы раздела диэлектриков 1 и 2 небольшой замкнутый прямоугольный контур ABCDA длины l, с направлением ориентации, как показано на рис. 1. По теореме о циркуляции вектора Е, применительно к данному случаю    откуда    (знаки интегралов по АВ и CD разные, поскольку пути интегрирования противоположны, а интегралы по участкам ВС и DA малы). 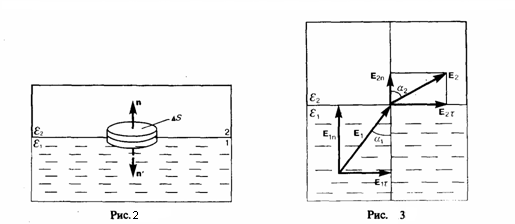Поэтому   (1)  Заменив проекции вектора Е проекциями вектора D, деленными на ε₀ε, получим   (2)  построим прямой цилиндр ничтожно малой высоты на границе раздела двух диэлектриков (рис. 2); одно основание цилиндра находится в первом диэлектрике, другое — во втором. Основания ΔS настолько малы, что в пределах каждого из них вектор D одинаков. Согласно теореме Гаусса для электростатического поля в диэлектрике    (нормали n и n' к основаниям цилиндра противоположно направлены). Поэтому   (3)  Заменив проекции вектора D проекциями вектора Е, умноженными на ε₀ε, получим   (4)  Значит, при переходе через границу раздела двух диэлектрических сред тангенциальная составляющая вектора Е(Е_τ) и нормальная составляющая вектора D(D_n) изменяются непрерывным образом (не испытывают скачка), а нормальная составляющая вектора Е(Е_n) и тангенциальная составляющая вектора D(D_τ) испытывают скачок.  Из условий (1) — (4) для составляющих векторов Е и D мы видим, что линии этих векторов испытывают излом (преломляются). Найдем как связаны между углы α₁ и α₂ (на рис. 3 α₁>α₂). Используя (1) и (4), Е_τ2 = Е_τ1 и ε₂E_n2 = ε₁E_n1. Разложим векторы E₁ и E₂ на тангенциальные и нормальные составляющие у границы раздела. Из рис. 3 мы видим, что    Учитывая записанные выше условия, найдем закон преломления линий напряженности Е (а значит, и линий смещения D)    Из этой формулы можно сделать вывод, что, входя в диэлектрик с большей диэлектрической проницаемостью, линии Е и D удаляются от нормали. 

14

Вещество или материальное тело, в котором имеются заряды, способные переносить электрический ток, называется проводником. В металлах переносчиками тока служат свободные (т.е. не привязанные к атомам) электроны, в электролитах — ионы, в плазме — и электроны, и ионы. Для электростатических явлений поле внутри проводника равно нулю:

15

15. Электрическая ёмкость. Конденсаторы.

Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.

В Международной системе единиц (СИ) ёмкость измеряется в фарадах.

Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид C=Q/φ, где Q — заряд,  φ— потенциал проводника.

Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара (или сферы) радиуса R равна (в системе СИ): C=4πεε0R, где ε0 — электрическая постоянная, ε — относительная диэлектрическая проницаемость. Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком или вакуумом, — к конденсатору. В этом случае ёмкость (взаимная ёмкость) этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна: C=εε0S/d, где S — площадь одной обкладки (подразумевается, что обкладки одинаковы), d — расстояние между обкладками, ε — относительная диэлектрическая проницаемость среды между обкладками, ε0 = 8.854·10−12 Ф/м — электрическая постоянная.

Конденса́тор — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. В простейшем варианте конструкции состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок. Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами (из-за намотки).