6 Поток вектора

В современной физике потоком вектора а называют скалярную физическую величину  Φ_а = ∫∫_S а dS = ∫∫_S (а n) dS , ( 1 )  где S – площадь произвольно расположенной поверхности;  а – произвольный вектор, начало которого лежит на поверхности S;  dS = n dS – псевдовектор, поставленный в соответствие ориентированной элементарной площадке (И.Бронштейн и К.Семендяев, 1968);  n – орт нормали к элементарной площадке dS.  Чаще всего приводится первая запись уравнения (1), но это не меняет того, что физическая величина Φ_а в уравнении (1) является скаляром. Псевдовектор элементарной площадки dS, является чистой математической абстракцией. В статье, посвященной физическому содержанию векторной величины, показано, что согласно принципу причинности произвольную векторную величину а следует рассматривать как локализациюполного вектора, распределенного по площади и приложенного в точке с заданными координатами.  Когда в математике и физике сначала вводят понятие частной величины (локального вектора), а затем – понятие общей величины, называемой потоком вектора, то мы имеем дело с не всегда оправданным применением индуктивного метода (от частного к общему). А дедуктивный метод (от общего к частному) предполагает сначала введение полной величины (неудачно названной в данном случае потоком вектора), а затем уже – введение локализованной величины (самого вектора).  Термин "поток вектора" является, по нашему мнению, отражением неаккуратности в присвоении названий физическим величинам и должен быть заменен другим термином. Процитируем популярный справочник по математике И.Бронштейна и К.Семендяева (1986): "Каждой ориентированной плоской площадке Σ можно поставить в соответствие вектор S, имеющий направление n и модуль, равный ее площади S ".  Приведем пример. На основании приведенной цитаты может показаться, что такая векторная величина, как перемещение объема ΔV, является скаляром, так как определяется скалярным произведением ΔV = хdS. Но приводимое в учебниках по физике указание на то, что "поток вектора скорости" является скалярной величиной, противоречит принципу причинности. Ведь перемещение x центра перемещаемого объема dVявляется следствием перемещения этого объёма, а не его причиной. При соблюдении принципа причинности следует записать выражение x = dV/dS. И тогда элементарная площадка dS остается скаляром, чем она, по сути дела, и является. А понятие о псевдовекторе площадки dS остается математической абстракцией, не имеющей физического содержания.  Почему же в теории физического поля применяются скалярные потоки вектора? Дело в том, что при анализе физического поля не применяются понятия о проточных системах и перемещаемых координатах состояния, и применение скалярных потоков вектора себя оправдывает теоретически, так как в этом случае оно не противоречит принципу причинности. Но и тут следует заметить, что вместо записи dS, как это принято в векторном анализе, предпочтительнее указывать запись ndS.  В частности, поток вектора магнитной индукции B (магнитный поток) Φ_m = ∫∫_S BndS является величиной скалярной, ведь в магнитных цепях никакие энергоносители не перемещаются. Это следует объяснять при преподавании, чтобы не казалось, будто в магнитных цепях что-то движется. А такие мысли могут появиться по причине того, что в термине "магнитный поток" присутствует слово "поток".

7

. Поток вектора электрического смещения через любую замкнутую поверхность, окружающую некоторый объем, равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности

 (15.11)

Вектор   – это такая характеристика поля, которая не зависит от диэлектрических свойств среды.

2. Так как  , то теорему Гаусса для однородной и изотропной среды можно записать:

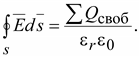(15.12)

Вектор   – это характеристика поля, которая зависит от диэлектрических свойств среды.

3. Поток вектора   через любую замкнутую поверхность создается не только суммой свободных зарядов, но и суммой связанных зарядов

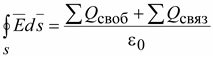. (15.13)

Теорему Гаусса можно использовать для нахождения напряженности или электрического смещения в какой-либо точке поля, если через эту точку можно провести замкнутую поверхность таким образом, что все ее точки будут в симметричных (одинаковых условиях по отношению к заряду, находящемуся внутри замкнутой поверхности).

Такой поверхностью являются обычно сфера (если заряд точечный), или боковая поверхность цилиндра (если заряд линейный).

8

Теорема Остроградского-Гаусса

Обозначим через G трехмерное тело, ограниченное кусочно-непрерывной, гладкой, замкнутой поверхностьюS с внешней нормалью. Предположим, что задано векторное поле компоненты которого имеют непрерывные частные производные.  Согласно формуле Остроградского-Гаусса, где через обозначена дивергенция векторного поля   (она обозначается также символом  ). Символ   указывает, что поверхностный интеграл вычисляется по замкнутой поверхности.  Формула Остроградского-Гаусса связывает поверхностные интегралы второго рода с соответствующими тройными интегралами.  Данную формулу можно записать также в координатной форме: В частном случае, полагая  , получаем формулу для вычисления объема тела G:

Пример 1

Вычислить поверхностный интеграл  , где S − внешне ориентированная поверхность сферы, заданная уравнением  . Решение. Используя формулу Остроградского-Гаусса, можно записать        Вычислим полученный тройной интеграл в сферических интегралах.

9

Теорема Гаусса выражает замечательное свойство электрического поля, которое позволяет представить эту теорему в иной форме, расширяющей ее возможности как инструмента исследования и расчета. Найдем дифференциальную форму теоремы Гаусса, в которой устанавливается связь между объемной плотностью заряда p иизменениями напряженности (E) в окрестности данной точки пространства.

Пусть имеем заряд q в объеме V, охватываемом замкнутой поверхностью S, представим его как

,

(12.1)

где < r> – среднее по объему V значение объемной плотности заряда. Запишем теорему Гаусса:

.

(12.2)

Тогда подставим это выражение в (12.1) и разделим обе части равенства на V. В результате получим:

.

(12.3)

Теперь устремим объем V®0, стягивая его к интересующей нас точке поля. Тогда <r> будет стремиться к значению r в данной точке поля, а левая часть уравнения будет стремиться к /₀.

Величину, являющуюся пределом отношения  Е dSк V при V0, называют дивергенцией поляЕ и обозначают divE. То есть, по определению:

.

(12.4)

Аналогично определяется дивергенция любого другого векторного поля. Из определения (12.4) следует, что дивергенция вектораEявляется скалярной функцией координат.

Чтобы найти дивергенцию Е надо взять бесконечно малый объем V, определить поток вектора Е сквозь замкнутую поверхность, охватывающую этот объем, и найти отношение этого потока к объему. Полученное выражение для дивергенции поля вектора Е будет зависеть от выбора системы координат (в разных системах координат оно оказывается разным). Если есть декартова система координат (x, y, z), то

.

(12.5)

Итак, мы выяснили, что при V0 в выражении (8.3) его правая часть стремится к /₀, а левая – к divE. Из (12.4) следует, что дивергенция поля Е связана с плотностью заряда в той же точке уравнением:

,

(12.6)

оно и выражает теорему Гаусса в дифференциальной форме.

В дифференциальной форме теорема Гаусса является локальной теоремой: дивергенция поля Е в данной точке зависит только от плотности электрического заряда r в той же точке и больше ни от чего.

Написание многих формул и действия с ними значительно упрощаются, если ввести векторный дифференциальный оператор Ñ (набла, или оператор Гамильтона), Под этим вектором подразумевается вектор с компонентами /x, /y, /z. Следовательно, в декартовой системе координат оператор Ñ имеет вид:

,

(12.7)

где i, j, k– орты осей x, y, z. Сам по себе вектор Ñ смысла не имеет. Он приобретает смысл только в сочетании со скалярной или векторной функцией, на которую он символически умножается. При умножении вектора набла на скаляр φ получим вектор –  . Если умножим вектор Ñ скалярно на вектор Е, то получим скаляр:

,

(12.8)

а это и есть по определению не что иное, как divE или ÑЕ. То есть дивергенция поля E скаляр и может быть записана как divEили ÑЕ (в обоих случаях читается как – «дивергенция вектора Е»).

Если умножить вектор   векторно на  , то получится вектор с компонентами:

,

которые совпадают с компонентами rot . Таким образом, существует два способа обозначений градиента, дивергенции и ротора:

;

;

.

Обозначения с помощью оператора   обладают рядом преимуществ, поэтому мы в дальнейшем и будем применять их. Например,

,

(12.9)

где Δ –оператор Лапласа;

,

(12.10)

(векторное произведение вектора самого на себя равно нулю);

,

(12.11)

(смешанное произведение векторов равно объёму параллелепипеда, построенного на перемножаемых векторах как на сторонах, если два из этих векторов совпадают, объём параллелепипеда равен нулю).

Теорема Гаусса теперь может быть записана в виде:

,

(12.12)

еще одна форма записи в дифференциальной форме теоремы Гаусса для электростатического поля в вакууме.

Дифференциальная форма записи электростатической теоремы Гаусса – это одно из замечательных свойств электрического поля. Т.е. в разных точках поля точечного заряда поле E отличается друг от друга, это же относится, вообще говоря, и к пространственным производным: E_x/x, E_y/y,  E_z/z . Однако, по утверждению теоремы Гаусса, сумма этих производных, которая определяет дивергенцию Е, оказывается во всех точках поля (вне самого заряда) равной нулю. В тех точках поля, где div E>0 (дивергенция Е положительна), мы имеем источники поля (положительные заряды), а там где она отрицательна – стоки (отрицательные заряды).

Линии вектора Е выходят из источников поля, а заканчиваются в местах стоков.

Теорема Остроградского-Гаусса:

 – это соотношение справедливо для любых векторных полей,   – векторная величина, характеризующая произвольное векторное поле.

 – теорема Стокса:

Циркуляция вектора   по произвольному замкнутому контуру Г равна потоку вектора rot   через произвольную поверхность S, ограниченную данным контуром.

Она позволяет найти циркуляцию вектора   по контуру Г, ограничивающему поверхность S (контур может быть не плоским), если известен ротор вектора   в каждой точке некоторой (не обязательно плоской) поверхности S.

Рассмотрим несколько интересных на наш взгляд примеров расчета напряженности или разности потенциалов для электростатического поля.
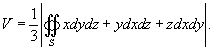
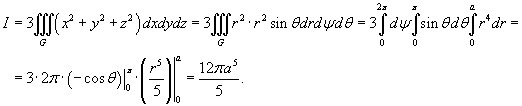
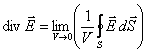