Д. Расчет круглых плитных фундаментов с учетом особенностей деформирования основания с переменными физико-механическими характеристиками

5.154. Предлагаемая методика используется для решения статических задач по расчету круглых плитных фундаментов, лежащих на линейно-деформируемом основании с переменными по глубине упругими характеристиками (модулем деформации и коэффициентом Пуассона ).

5.155. Расчет плит может производиться как на основе теории тонких изгибаемых пластин (теории Кирхгоффа), так и на основе теории пластин средней толщины (теории Рейсснера).

Толщина плитного фундамента считается постоянной, материал - изотропным.

Допустимыми для расчета нагрузками могут быть только нагрузки, симметричные относительно центра:

вертикальная равномерно распределенная нагрузка по кругу (в том числе и по всей плите) или по кольцу;

вертикальная равномерная силовая нагрузка по окружности (в том числе и по краю плиты);

равномерная моментная нагрузка по окружности (в том числе и по краю плиты);

сосредоточенная сила в центре плиты;

горизонтальные растягивающие (сжимающие) усилия, приложенные по краю плиты.

Трение между плитой и основанием не учитывается.

Связи между плитой и основанием вертикальные, двусторонние.

5.156. На основе сделанных предпосылок (пп.5.154, 5.155) задача о расчете круглых плитных фундаментов на линейно-деформируемом основании математически может быть сформулирована в виде следующих уравнений, записанных в полярной системе координат:

; (336)

; (337)

; (338)

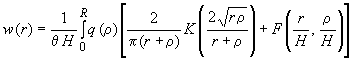(339)

,

где - прогиб плиты;

- радиус плиты;

- заданная внешняя нагрузка;

- контактное давление на плиту со стороны основания;

- дифференциальный оператор изгиба плиты.

Для тонких плит при вертикальной нагрузке

,

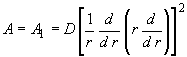где - цилиндрическая жесткость плиты на изгиб; - коэффициент Пуассона.

Для тонких плит при одновременном действии вертикальных и горизонтальных усилий

,

где - горизонтальные усилия, распределенные по краю срединной плоскости плиты.

Для плит средней толщины, рассчитываемых по теории Рейсснера,

.

, - граничные условия для плиты. Чаще всего это условия свободного края. В интегральном уравнении (339) имеет размерность напряжения и характеризует упругие свойства основания. имеет размерность длины и является основной геометрической характеристикой основания. - эллиптический интеграл первого рода. Функция имеет вид

,

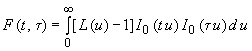где - функция, определяемая выбранной моделью линейно-деформируемого основания.

Для однородного упругого полупространства 1.

В случае модели линейно-деформируемого основания с произвольно изменяющимися по глубине упругими характеристиками функция задается численно, если аналитическое ее представление невозможно.

Метод решения поставленной задачи основан на использовании специальных ортонормированных полиномов, позволяющих сопрягать решения дифференциального уравнения относительно прогиба плиты (336) и интегрального уравнения для расчета отпора упругого основания (339).

Решение проводится в три этапа.

На первом этапе строится специальная система полиномов , удовлетворяющих граничным условиям (337), (338) и ортонормированных по отношению к дифференциальному оператору , описывающему деформацию плиты, т.е. полученная ортогональная система полиномов удовлетворяет следующему условию:

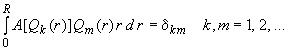(340)

;

- символ Кронеккера.

Функция прогиба представляется в виде ряда по полиномам

. (341)

На втором этапе строится решение интегрального уравнения (339).

При этом, учитывая линейность задачи, контактное давление может быть представлено в виде линейной комбинации частных решений с теми же коэффициентами, что и функция прогиба:

. (342)

После подстановки рядов (341) и (342) в интегральное уравнение (339) и приведения последнего к безразмерному виду получим интегральных уравнений для определения :

,

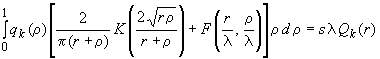(343)

где безразмерный параметр характеризует жесткость плиты и основания, . Для решения интегральных уравнений (343) использован метод сведения каждого из них к бесконечной алгебраической системе уравнений с помощью разложения функций , , в ряды по собственным функциям главной части интегрального оператора.

На третьем этапе происходит сопряжение решений для прогиба плиты (341) с решением соответствующей контактной задачи (342). При этом ряды (341) и (342) подставляем в дифференциальное уравнение изгиба плиты (336) и с учетом условия ортогональности (340) и условия статики приходим к бесконечной линейной алгебраической системе уравнений для определения коэффициентов .

Зная , можно по формуле (341) найти прогибы плиты и другие характеристики рассматриваемой задачи.

Изложенный алгоритм реализован в виде вычислительной программы на языке ФОРТРАН для ЭВМ типа ЕС-1022.

Программа позволяет определять напряженно-деформированное состояние плиты в широком диапазоне изменения параметров , при различных моделях основания и видах нагружения.

Пример. В качестве модели основания рассматривается слой, свободно лежащий на упругом полупространстве:

,

, где , характеризуют механические свойства слоя и полупространства; , - соответственно модуль сдвига и коэффициент Пуассона материала слоя и полупространства.

Анализ результатов расчета показывает, что в центральной зоне плиты отпор основания значительно уменьшается с увеличением параметра и уменьшением относительной толщины верхнего слоя. При некоторых соотношениях параметров , , отпор основания становится отрицательным как при равномерно распределенной, так и при сосредоточенной нагрузке.

Так, например, для 1, 5, 1 отпор основания и изгибающий момент при равномерно распределенной нагрузке 1 в центре плиты имеют значения: 0,101, 0,139.

Результаты приведены в безразмерном виде.

Размерные величины нагрузки , отпора , момента можно получить по формулам:

, ,

.