Г. Расчет круглых и кольцевых плитных фундаментов сооружений башенного типа с учетом особенностей деформирования железобетона

5.146. Указания раздела относятся к круглым и кольцевым плитным фундаментам под дымовые трубы или иные отдельно стоящие, круглые в плане сооружения башенного типа.

5.147. Изгибающие моменты в плитном фундаменте определяются с учетом образования трещин, нелинейных деформаций железобетона и вызываемого ими перераспределения усилий, а также с учетом жесткости надфундаментного строения. Расчетная схема фундамента приведена на рис.65. Действующая на плитный фундамент нагрузка приводится к погонной осесимметричной нагрузке (см. рис.65), определяемой по формуле

, (300)

где - равнодействующая вертикальной нагрузки на плитный фундамент от веса сооружения вместе со стаканом фундамента;

- результирующий момент внешних сил относительно подошвы плитного фундамента;

- радиус приложения нагрузки .

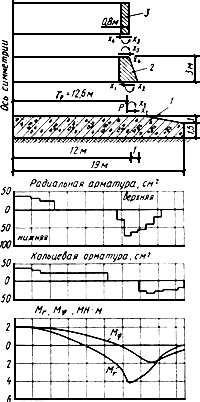
Рис.65. Расчетная схема и результаты расчета

1 - плитный фундамент; 2 - стакан фундамента; 3 - подфундаментное строение

Неизвестные усилия в местах сопряжений стакана фундамента с плитой и надфундаментным строением (см. рис.65) находятся из условий совместности деформаций. При этом стакан фундамента и надфундаментное строение допускается считать линейно-упругими.

Для основания принимается расчетная схема по указаниям разд.1 в виде линейно-деформируемого слоя, либо основания, подчиняющегося гипотезе переменного коэффициента жесткости, либо как комбинация этих схем.

Расчет плитного фундамента производится на ЭВМ вариационно-разностным методом путем последовательных приближений. В каждом приближении производится расчет анизотропного линейно-упругого плитного фундамента, жесткости которого определяются по результатам предыдущего приближения в соответствии с указаниями пп.5.148 и 5.149. В первом приближении плитный фундамент предполагается изотропным, а его жесткости вычисляются по формуле (304). Процесс последовательных приближений заканчивается, когда разница в кривизнах для двух соседних приближений будет составлять не более 2%.

Для обеспечения необходимой точности расчета плитный фундамент следует разбивать разностными узлами не менее чем на 20 участков по радиусу.

5.148. Элемент плиты может находиться в одной из четырех стадий работы: линейно-упругой; упругопластической без трещин; упругопластической с трещинами; предельной.

Уравнения, устанавливающие связь между изгибающими моментами и кривизнами, для всех стадий записываются в виде:

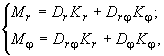* (301)

где и - радиальный и окружной изгибающие моменты;

*, , - жесткости;

*, - радиальная и окружная кривизны, определяемые по формулам:

;

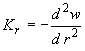, (302)

в которой - функция прогибов;

- текущий радиус.

__________________

* Формула и экспликация к ней соответствуют оригиналу. - Примечание изготовителя базы данных.

1-я стадия ограничивается неравенствами:

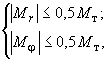(303)

где - изгибающий момент трещинообразования, определяемый по формуле

,

где - толщина элемента плиты;

- расчетное сопротивление бетона осевому растяжению для предельного состояния второй группы.

В 1-й стадии жесткости вычисляются следующим образом:

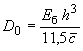, , , (304)

где 0,2 - коэффициент поперечной деформации бетона;

- начальный модуль упругости бетона;

- коэффициент, учитывающий влияние длительной ползучести бетона, определяемый по формуле

, (305)

- коэффициент, принимаемый равным 2 при влажности окружающей среды выше 40% и равным 3 при влажности окружающей среды 40% и ниже;

- коэффициент длительности действия нагрузки, определяемый по формуле

, (306)

где - часть полной нагрузки , включающая в себя постоянные и длительные нагрузки.

2-я стадия наступает, когда оба изгибающих момента по абсолютной величине не превышают , но хотя бы один из них превосходит 0,5 . Жесткости при этом определяются следующим образом:

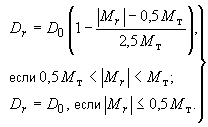(307)

Жесткость определяется аналогично заменой индекса на , а вычисляется по формуле

. (308)

3-я стадия достигается, когда один из моментов или превысит момент трещинообразования. Предполагается, что по площадке действия этого момента появляется трещина. При дальнейшем увеличении нагрузки второй момент также может достичь трещинообразования и появятся трещины второго направления. Жесткости для третьей стадии работы элемента плиты определяются по формулам:

,

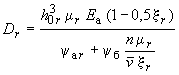если ; (309)

,

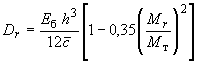если . (310)

Жесткость определяется аналогично, заменой индекса на , а 0.

В этих формулах:

- полезная высота сечения;

- коэффициент армирования;

- модуль упругости арматуры;

;

- относительная высота сжатой зоны бетона в сечении с трещиной;

- коэффициент, учитывающий работу растянутого бетона на участке с трещинами;

- коэффициент, учитывающий неравномерность деформаций сжатой грани сечения и принимаемый равным 0,9;

- коэффициент, учитывающий снижение модуля деформации бетона сжатой зоны.

Параметры и являются функциями соответствующих изгибающих моментов или . Относительная высота сжатой зоны определяется по формуле

, (311)

где - предельный изгибающий момент, который может воспринять сечение, определяемый по формуле

; (312)

и - расчетные сопротивления арматуры растяжению и бетона осевому сжатию для предельных состояний второй группы

; (313)

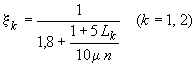; (314)

; ; ;

3, если ;

5, если .

Коэффициент вычисляется по формуле

, (315)

но принимается не более 1.

Здесь - коэффициент, учитывающий длительность действия нагрузки и определяемый по формуле

. (316)

Коэффициент определяется по формуле

, (317)

где - коэффициент, принимаемый равным 0,15 при влажности окружающей среды выше 40% и равным 0,1 при влажности окружающей среды 40% и ниже.

4-я стадия работы элемента плиты наступает, когда одна из кривизн или достигает своего критического значения или , определяемого по формулам для третьей стадии при значениях соответствующих изгибающих моментов, равных или . Предполагается, что при образуется кольцевая (радиальная) линия излома. В сечении, совпадающем с линией излома, напряжения в арматуре достигают , напряжения в бетоне сжатой зоны , а увеличение кривизны в направлении, перпендикулярном линии излома, происходит при постоянном значении соответствующего изгибающего момента, равного предельному (рис.66).

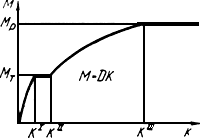
Рис.66. Диаграмма деформирования железобетона

Жесткости в этой стадии определяются по формулам:

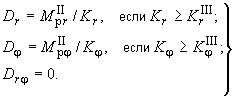(318)

Если одна из кривизн меньше своего критического значения, то соответствующая жесткость вычисляется по формулам (309)-(310).

5.149. При расчете плитного фундамента жесткости для ( +1) приближения определяются по кривизнам предыдущего приближения .

Для этого вначале определяются характерные кривизны диаграммы деформирования для каждого узла разностной сетки в радиальном и окружном направлениях: - максимальная кривизна в направлении (или ), когда имеются только радиальные (или только кольцевые) трещины; - кривизна в направлении , соответствующая началу упрочнения на диаграмме деформирования; - кривизна, соответствующая образованию линий излома. Характерные кривизны вычисляются по формулам:

; (319)

; (320)

, (321)

где - вычисляется по формуле (309) при ; - вычисляется по формуле (309) при .

При вычислении характерных кривизн следует учитывать, что их величины будут зависеть от того, какие волокна растягиваются - верхние или нижние. В соответствии с этим в расчет надо вводить либо верхнюю, либо нижнюю арматуру.

При вычислении жесткостей стадия работы элемента плитного фундамента определяется по его кривизнам. Если выполняется хоть одно из условий

; , (322)

где , - кривизны -го приближения, то при определении жесткостей ( +1)-го приближения предполагается, что элемент работает с трещинами. В этом случае 0, а диаграмма деформирования имеет вид, изображенный на рис.66. Жесткости для ( +1)-го приближения и вычисляются по формуле

. (323)

Изгибающий момент в формуле (323) определяется следующим образом.

Если

, то .

Если , то и образуется кольцевая (радиальная) линия излома.

На участках и (см. рис.66) может быть определен методом хорд с использованием соответственно формулы (310) и формулы (309) для описания диаграммы деформирования.

Если не выполняется ни одно из условий (322), то жесткости для ( +1)-го приближения вычисляются по формулам:

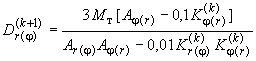; (324)

, (325)

где .

При выводе этих формул использовалась система уравнений (301) и предполагалось, что для жесткостей и справедлива формула (307). Если значения или по формуле (324) получаются больше, чем , то их следует принять равными . Если или получаются меньше, чем 0,8 , то это означает, что элемент плиты работает с трещинами. В этом случае следует принять 0, а жесткости и вычислять по формуле (323).

5.150. Рабочая арматура плитного фундамента должна обеспечивать его прочность и допустимую ширину раскрытия трещин. Кроме того, количество арматуры в сечениях с трещинами должно обеспечивать выполнение условия

, (326)

где - предельный изгибающий момент в сечении при расчете на прочность, определяемый по формуле (312) при характеристиках бетона и арматуры для предельных состояний первой группы.

Следует учитывать, что усилия в плитном фундаменте при определении их с учетом нелинейных деформаций железобетона существенно зависят от принятого армирования. Поэтому подбор арматуры следует выполнять методом последовательных приближений. Предварительные размеры участков армирования и количество арматуры в сечениях могут назначаться из линейного расчета с последующим корректированием их по усилиям нелинейного расчета.

Допускается не ставить рабочей арматуры в сечениях, где не образуется трещин при расчете по прочности, т.е. выполняется условие

, (327)

где - изгибающий момент в сечении от действия нагрузки с коэффициентом перегрузки больше единицы;

0,9 - коэффициент условий работы;

- расчетное сопротивление бетона осевому растяжению для предельных состояний первой группы.

5.151. Расчет плитного фундамента по прочности должен выполняться на действие нагрузки с коэффициентом перегрузки больше единицы. Если радиальный (окружной) изгибающий момент превосходит соответствующее значение , то предполагается образование кольцевой (радиальной) линии излома. Следует считать, что прочность фундамента обеспечена, если радиальные и кольцевые линии излома не образуют областей, делящих его на отдельные части.

5.152. Плитный фундамент должен рассчитываться на раскрытие вертикальных трещин в радиальных и окружных сечениях при выполнении условия

, (328)

где - изгибающий момент в сечении от действия нагрузки с коэффициентом перегрузки равным единице.

Ширину кратковременного раскрытия трещин следует вычислять по формуле

. (329)

Ширину длительного раскрытия трещин следует вычислять по формуле

. (330)

В формулах (329) и (330):

- ширина раскрытия трещин от кратковременного действия нагрузки ;

, - коэффициенты, учитывающие работу растянутого бетона над трещинами в слабоармированных сечениях ( 0,008);

- коэффициент, принимаемый равным 1,5 для фундаментов, эксплуатируемых выше уровня грунтовых вод, и равным 1,2 для фундаментов, эксплуатируемых ниже уровня грунтовых вод.

Ширина раскрытия трещин от кратковременного действия нагрузки , мм, должна определяться по формуле

, (331)

где - напряжение в растянутой арматуре, вычисляемое по формуле

, (332)

в которой вычисляется согласно указаниям п.5.148;

- модуль упругости арматуры;

- диаметр растянутой арматуры, мм.

Коэффициент , учитывающий уровень нагружения, вычисляется по формуле

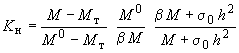, (333)

где - изгибающий момент, при котором растянутый бетон над трещинами практически выключается из работы, равный:

, (334)

но не более 3,3 ;

- коэффициент, принимаемый равным 1 при вычислении и равным при вычислении ; 0,17 МПа.

Коэффициент , учитывающий длительность действия нагрузки, определяется по формуле

. (335)

Коэффициенты и принимаются равными единице, если не выполняется хоть одно из условий:

;

;

.

5.153. По описанному алгоритму разработана программа АРПОС-2 для ЕС ЭВМ. Программа позволяет делать поверочный расчет либо подбирать армирование из условий прочности плитного фундамента и допустимой ширины раскрытия трещин. В качестве моделей основания используются упругий слой, модель с переменным по радиусу коэффициентом жесткости и комбинация этих двух моделей. Программа написана на ФОРТРАНе и требует ЭВМ с объемом внутренней памяти не менее 128 К.

Пример

Подобрать армирование для плитного фундамента, изображенного на рис.65. 200 МН; 500 МН·м; коэффициенты перегрузки 1,1; 1,3. Основание - слой толщиной 14 м с модулем упругости 30 МПа (с учетом коэффициента условий работы основания 1,5). Бетон М 300; арматура A-III диаметром 28 мм. Фундамент находится ниже уровня грунтовых вод. Предельная ширина раскрытия трещин: длительная - 0,2 мм, кратковременная - 0,3 мм. Результаты расчета приведены на рис.65.