Расчет кольцевого плитного фундамента на сжимаемом основании

5.136. Указания раздела относятся к расчету осесимметрично загруженной кольцевой плиты переменной толщины со свободными краями, лежащей на линейно-упругом, винклеровском основании.

5.137. При расчете кольцевой плиты следует принять следующие допущения:

деформации плиты описываются уравнениями технической теории тонких пластин (теория Кирхгоффа);

реакция упругого основания направлена вертикально вверх и пропорциональна упругому перемещению нижней поверхности кольца;

материал плиты изотропный и линейно-упругий;

силы трения между плитой и основанием отсутствуют;

связи между плитой и основанием вертикальные двусторонние.

5.138. Для расчета кольцевого плитного фундамента следует использовать расчетную схему, приведенную на рис.63, а, принимая положительные направления внутренних усилий и перемещений в соответствии с рис.63, а, б, в.

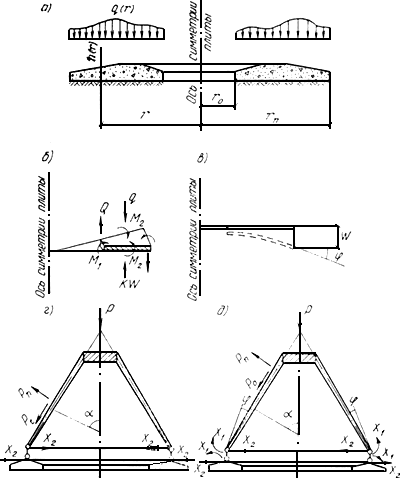
Рис.63. К расчету кольцевой или круглой плиты конечной жесткости и системы

в форме конической оболочки, сопряженной с плитой конечной жесткости

а - схема загружения кольцевой плиты; б - направления внутренних усилий;

в - то же, перемещений; г - основная система фундамента в форме конической оболочки,

сопряженной неподвижным шарниром с плитой конечной жесткости; д - основная система

фундамента в форме конической оболочки, жестко защемленной в плите конечной жесткости

5.139. Дифференциальное уравнение изгиба плиты имеет следующий вид:

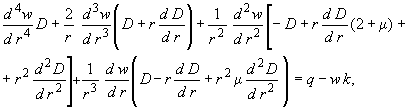(285)

где - коэффициент жесткости основания; - модуль упругости материала плиты; - коэффициент Пуассона материала плиты; - толщина плиты; - вертикальное смещение срединной линии плиты; - внешняя осесимметричная, непрерывно распределенная нагрузка.

Зависимости для определения усилий в кольцевом плитном фундаменте имеют вид:

; (286)

; (287)

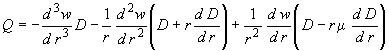. (288)

В формулах (286)-(288) , - изгибающие моменты в радиальном и кольцевом направлениях соответственно;

- поперечная сила.

Граничные условия при и выражаются формулами:

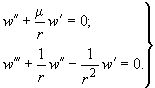(289)

5.140. Расчет кольцевой плиты переменной толщины следует выполнять с использованием метода Рунге-Кутта.

Общее решение дифференциального уравнения (285) следует представить в виде

, (290)

где - следующие частные решения для однородного уравнения с начальными условиями:

при

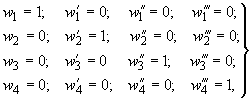(291)

- частное решение неоднородного уравнения с нулевыми начальными условиями:

; (292)

, , , - произвольные постоянные, определяемые из граничных условий (289).

Задачи Коши нахождения частных решений , , , , решаются методом Рунге-Кутта.

По краевым условиям формулы (289) составляется система из 4 линейных уравнений для определения произвольных постоянных.

Круглый фундамент переменной толщины программой расчета аппроксимируется кольцевой плитой, сопряженной с жесткой вставкой в центре.

Граничные условия выражаются формулами:

при

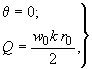(293)

где при ( - малая конечная величина, определяемая программой),

или

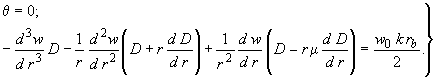(294)