
- •Руководство по проектированию плитных фундаментов каркасных зданий и сооружений башенного типа
- •Предисловие
- •1. Основные положения Общие указания
- •Требования к инженерно-геологическим изысканиям
- •Требования к расчетам плитного фундамента и основания
- •2. Расчет основания по деформациям
- •Выбор расчетной схемы и параметров основания
- •Определение осадок основания
- •Определение крена плитного фундамента
- •3. Определение предварительных размеров плитного фундамента по условию минимального объема бетона
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Поперечные силы
- •Вводы в табл.24-42
- •4. Определение коэффициентов жесткости основания плитного фундамента
- •Реактивные давления
- •Реактивные давления
- •Реактивные давления
- •Реактивные давления
- •Реактивные давления
- •Реактивные давления
- •Реактивные давления
- •Реактивные давления
- •Реактивные давления
- •Реактивные давления
- •Реактивные давления
- •5. Статические расчеты плитных фундаментов
- •А. Расчет плитных фундаментов произвольной формы в плане для каркасных зданий Расчет плитного фундамента с учетом влияния стен здания
- •Элементарные операторы для формирования уравнений (62)
- •Расчет плитного фундамента здания с учетом особенностей деформирования железобетона
- •Элементарные операторы для формирования разрешающих уравнений при расчете плиты с учетом особенностей деформирования железобетона
- •Совместный расчет плитного фундамента и рамного каркаса здания
- •Результаты подбора арматуры в фундаменте
- •Совместный расчет плитного фундамента и элементов надфундаментного строения здания со связевым или рамно-связевым каркасом, а также панельного и кирпичного дома
- •Расчет плитных фундаментов с учетом влияния рамного каркаса здания Расчет фундамента совместно с рамным каркасом
- •Расчет прямоугольных плитных фундаментов зданий с рамным каркасом при учете жесткости каркаса и реактивных касательных напряжений
- •Расчет прямоугольных плитных фундаментов зданий со связевым каркасом при учете реактивных касательных напряжений
- •Расчет толстых плитных фундаментов с учетом реактивных касательных напряжений
- •Расчет сплошных железобетонных плитных фундаментов под сетку колонн по кинематическому методу предельного равновесия
- •Б. Расчет плитных фундаментов произвольной формы в плане для силосных корпусов Расчет плитных фундаментов с учетом жесткости силосных корпусов
- •Совместный расчет плитных фундаментов элеваторов и надфундаментных конструкций конечной жесткости
- •Расчет прямоугольного плитного фундамента, взаимодействующего с деформируемым основанием и жестким надфундаментным строением (типа силосного корпуса)
- •В. Расчет круглых и кольцевых плитных фундаментов с коническими оболочками для сооружений башенного типа
- •Расчет конической оболочки, опертой на сжимаемое основание
- •Расчет конической оболочки, опертой в нижнем сечении на абсолютно жесткое основание при различных типах опирания
- •Расчет кольцевого плитного фундамента на сжимаемом основании
- •Совместный расчет конической оболочки и кольцевой плиты конечной жесткости на сжимаемом основании
- •Расчет конической оболочки, лежащей на сжимаемом основании, подкрепленной опорным кольцом
- •Г. Расчет круглых и кольцевых плитных фундаментов сооружений башенного типа с учетом особенностей деформирования железобетона
- •Д. Расчет круглых плитных фундаментов с учетом особенностей деформирования основания с переменными физико-механическими характеристиками
- •6. Конструктивные требования
- •7. Требования к измерениям осадок, сдвигов и кренов фундаментов плит
- •Измерение осадок
- •114 Мм, толщиной 4 мм, длиной а (гост 10704-76* ); 6 - полусфера радиусом 40 мм из стали Ст5
- •Измерение сдвигов
- •Измерение кренов
- •Обработка результатов измерений
- •Характеристики программ для расчета плитных фундаментов на эвм
- •Определение осадок и кренов прямоугольных фундаментов на линейно-деформируемом полупространстве и слое конечной толщины с использованием графиков
- •Определение осадок и кренов круглого фундамента на линейно-деформируемом полупространстве и слое конечной толщины с использованием графиков
Расчет конической оболочки, опертой в нижнем сечении на абсолютно жесткое основание при различных типах опирания
5.131. Требования раздела относятся к расчету осесимметричной конической оболочки переменной толщины, верхнее сечение которой представляет собой жесткий диск, нижнее сечение опирается на жесткое основание.
5.132. При расчете оболочки
следует принимать допущения, изложенные
в п.5.127, за исключением допущений о
реакциях основания (
0,
![]() 0).
0).
5.133. Расчет оболочки должен производиться на следующие типы нагрузок:
сосредоточенная вертикальная сила вдоль оси оболочки;
осесимметричная, распределенная по поверхности оболочки, меняющаяся по линейному закону вдоль образующей конуса;
краевые осесимметричные нагрузки (силовые и деформационные), различные для каждого типа опирания.
5.134. Расчет конической оболочки следует производить с использованием системы разрешающих уравнений:
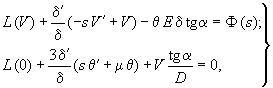 (272)
(272)
где
![]() .
(273)
.
(273)
Значения
,
![]() ,
,
![]() ,
,
,
в уравнениях (272) те же, что в п.5.130.
,
,
,
в уравнениях (272) те же, что в п.5.130.
Усилия, деформации, вертикальные и горизонтальные перемещения оболочки определяются по зависимостям (260)-(269), а нормальное перемещение - по формуле
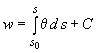 .
(274)
.
(274)
Положительное направление усилий должно приниматься в соответствии с рис.61, б и 62, а, б, в, г.
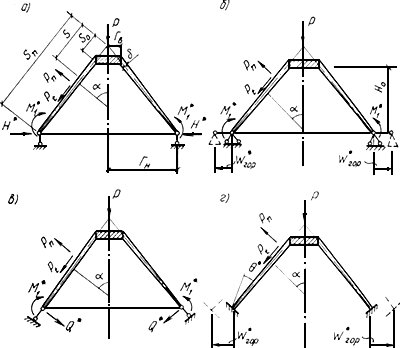
Рис.62. Типы опирания конической оболочки на жесткую плиту
а - подвижный шарнир; б - неподвижный шарнир; в - подвижный шарнир,
реакция опоры которого направлена вдоль образующей; г - жесткое защемление
Для конических оболочек граничные условия на верхнем краю следует принимать:
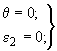 (275)
(275)
или через переменные
![]() ,
:
,
:
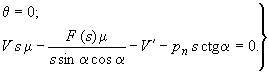 (276)
(276)
5.135. Различные типы опирания
оболочки и различные виды краевой
нагрузки отражаются на краевых условиях
для нижнего сечения оболочки. Эти условия
при
![]() следует принять в виде:
следует принять в виде:
а) 1-й тип опирания (рис.62, а)
при заданных
![]() и
и
![]() :
:
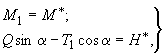 (277)
(277)
или через переменные и :
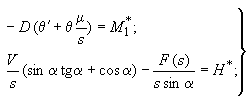 (278)
(278)
б) 2-й тип опирания (рис.62, б)
при заданных
,
![]() :
:
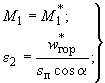 (279)
(279)
или через переменные и :
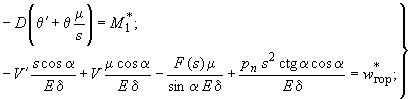 (280)
(280)
в) 3-й тип опирания (рис.62, в)
при заданных
и
![]() :
:
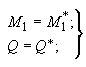 (281)
(281)
или через переменные , :
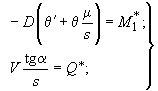 (282)
(282)
г) 4-й тип опирания (рис.62, г)
при заданных
![]() и
:
и
:
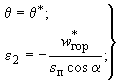 (283)
(283)
или через переменные , :
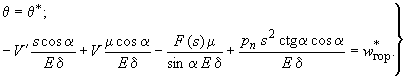 (284)
(284)
При отсутствии усилий, перемещений и деформаций на нижнем краю величины со звездочкой следует положить равными нулю.
Краевую задачу для рассмотренных случаев следует решать с использованием разностных методов.
