Б. Расчет плитных фундаментов произвольной формы в плане для силосных корпусов Расчет плитных фундаментов с учетом жесткости силосных корпусов
5.94. Указания раздела относятся к расчету плитных фундаментов полигонального очертания в плане постоянной либо ступенчато-переменной толщины при действии произвольной нагрузки с учетом и без учета влияния жесткости силосных корпусов.
5.95. При расчете плиты принимаются следующие допущения:
деформации плиты описываются уравнениями технической теории тонких изгибаемых пластин (теория Кирхгоффа) либо пластин средней толщины (теория Рейсснера);
плита изотропная, материал плиты и основания линейно-упругий;
при наличии ребер плита считается конструктивно анизотропной;
вертикальные перемещения точек плиты и основания одинаковы;
силы трения между плитой и основанием отсутствуют.
5.96. Расчет плиты производится на следующие типы нагрузок и воздействий:
равномерно распределенные по прямоугольной площадке вертикальные нагрузки;
сосредоточенные по линии погонные вертикальные силы и моменты;
сосредоточенные в точках вертикальные силы;
нагрузки, приходящиеся на верхнее строение;
смещения опертых краев плиты и повороты в заделках.
5.97. Для основания следует использовать расчетную схему, характеризуемую переменным коэффициентом жесткости, либо в виде линейно-деформируемого слоя, приближенно описываемого двумя коэффициентами жесткости (см. разд.1).
5.98. При наличии жесткого верхнего строения (силосный корпус, соединяемый с плитой системой упругодеформируемых стоек) производится совместный расчет плиты и жесткого верхнего строения.
5.99. Расчет фундаментной плиты по указаниям настоящего раздела допускает учет наличия свайного поля с дискретным расположением свай в расчетной схеме, для чего должны быть заданы информация о расположении свай и характеристики податливости свай (смещение оголовка сваи в вертикальном направлении от действия единичной силы, угол поворота оголовка сваи от действия единичного момента).
5.100. Для расчета плитного фундамента рационально использовать метод конечных элементов в варианте метода перемещений.
Потенциальная энергия системы "плита+основание" представляется в виде зависимости (56).
Выражение для потенциальной энергии деформации изгибаемой плиты , входящей в формулу (56), зависит от принятых гипотез, используемых при выводе разрешающих уравнений изгиба плиты. Для тонких анизотропных плит (теория Кирхгоффа) это выражение имеет вид
,
(216)
где
- область плоскости
,
занимаемая плитой;
- компоненты тензора анизотропии;
- функция прогибов (перемещений) плиты.
Здесь и далее нижними индексами после запятой помечаются производные, взятые по соответствующей координате, например:
,
.
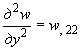В формуле (216) и далее используется соглашение о суммировании по повторяющимся индексам. Все индексы пробегают значения от 1 до 2, причем 1 соответствует направлению вдоль оси , а 2 - вдоль оси .
В случае изотропной плиты
,
(217)
где
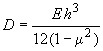- цилиндрическая жесткость плиты при
изгибе;
- модуль упругости материала плиты;
- толщина плиты;
- коэффициент Пуассона;
- символ Кронекера.
Выражение для в случае изотропной плиты имеет вид
.
(218)
Для изотропных плит средней толщины (теория Рейсснера) выражение для записывается в виде
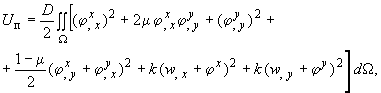
где помимо уже введенных обозначений положено
,
(219)
причем
,
- углы поворота нормали к срединной
поверхности плиты относительно осей
и
соответственно. Положительные направления
перемещения
и поворотов
и
показаны на рис.47.
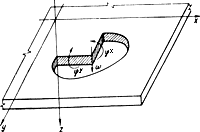
Рис.47. Положительные направления перемещения и углов поворота ,
Для тонких плит (теория Кирхгоффа) имеют место соотношения:
,
.
(220)
Выражение для зависит от принимаемой расчетной схемы основания. Для основания с двумя коэффициентами постели имеет вид
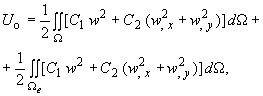(221)
где
- область плоскости
внешняя к области
,
т.е.
есть дополнение
до всей плоскости
.
Интеграл по
в выражении (221) учитывает работу основания
за пределами плиты. В случае основания,
описываемого переменным коэффициентом
жесткости, в выражении (221) пропадает
интеграл по
и, кроме того, полагается
0.
Падение потенциала внешних сил (работа внешних сил на статически соответствующих им перемещениях) определяется выражением
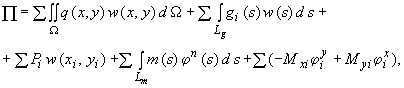(222)
где
- распределенная по площади нормальная
к срединной поверхности плиты нагрузка;
- погонная, распределенная по линии
нагрузка;
- сосредоточенная сила, действующая на
плиту в точке с координатами
;
- погонный, распределенный по линии
момент;
,
- сосредоточенные моменты относительно
осей
и
,
соответственно действующие на плиту в
точке с координатами
,
;
- угол поворота нормали к срединной
поверхности плиты вокруг оси
.
Положительные направления действующих на плиту нагрузок показаны на рис.48.
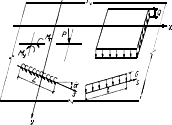
Рис.48. Положительные направления действующих на плиту нагрузок
При решении задачи по методу конечных элементов исходная континуальная задача минимизации функционала полной потенциальной энергии системы приближенно заменяется дискретной задачей, решение которой сводится к решению системы линейных алгебраических уравнении, т.е. система с бесконечным числом степеней свободы заменяется системой с конечным числом степеней свободы. Процедура дискретизации заключается в том, что вся область интегрирования представляется в виде объединения непересекающихся областей:
,
.
(223)
Отдельная область
интегрирования
составляет при этом так называемый
"конечный" элемент. При этом
,
(224)
где
- полная потенциальная энергия,
накапливаемая в отдельном конечном
элементе, причем
.
(225)
В пределах конечного элемента прогиб аппроксимируется линейным агрегатом вида
,
(226)
где функции
определены только на
-м
элементе. Параметры
выражаются через перемещения и некоторое
количество производных от перемещения
в узловых точках конечного элемента. В
случае плит средней толщины принимается
независимая аппроксимация прогибов и
углов поворота.
Используя результаты подстановки в формулу (226) значений , выраженных через узловые перемещения, по формуле (225) получаем
,
(227)
где
- матрица жесткости конечного элемента;
- грузовой вектор;
- вектор узловых перемещений конечного
элемента, размерность которого
определяется числом степеней свободы
этого конечного элемента, причем
,
(228)
где
- матрица жесткости конечного элемента
плиты;
- матрица жесткости соответствующего
конечного элемента упругого основания.
Полная потенциальная энергия дискретной системы принимает вид
,
(229)
где - общее количество конечных элементов.
Из условия минимума полной потенциальной энергии системы в положении равновесия получается дискретное разрешающее уравнение в виде
,
(230)
где
- полная матрица жесткости системы;
- полный грузовой вектор;
- вектор обобщенных перемещений всех
узлов системы.
Матрица жесткости
набирается суммированием из элементов
матриц жесткостей
отдельных конечных элементов, причем
в каждом узле системы суммируются
компоненты матриц
,
относящихся к элементам, сходящимся в
данном узле. Например, для узла
на рис.49 компоненты соответствующего
блока матрицы
набираются суммированием из компонентов
матриц
,
,
,
.
Аналогично компоненты полного грузового
вектора
набираются суммированием из элементов
векторов
.
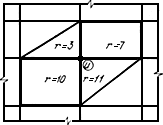
Рис.49. Конечные элементы,
сходящиеся в узле
5.101. Для расчета плит с учетом влияния верхнего строения следует использовать смешанный метод расчета. При этом вводятся следующие предпосылки:
верхнее строение рассматривается в расчетной схеме как твердое недеформируемое тело;
верхнее строение соединяется с плитой системой упругодеформируемых стоек;
стойки верхнего строения обладают конечной жесткостью на сжатие и изгиб и не сопротивляются закручиванию.
5.102. Основная система смешанного метода расчета образуется отделением верхнего строения (вместе со стойками) от плиты и наложением дополнительных связей на верхнее строение, устраняющих жесткое его смещение. Неизвестными смешанного метода расчета являются усилия в стойках верхнего строения и перемещения наложенных связей.
5.103. Окончательные результаты расчета плиты получаются суммированием величин, получаемых от действия внешних нагрузок и от усилий, передающихся от стоек верхнего строения.
Пример расчета плитного фундамента силосного корпуса по программе КОРПУС-ЕС.
Требуется выполнить расчет
прямоугольного в плане плитного
фундамента, лежащего на сжимаемом
основании. Жесткое верхнее строение
соединено с фундаментом стойками, центры
которых показаны на рис.50. К заштрихованной
части фундамента приложена равномерно
распределенная нагрузка с равнодействующей
2000
кН. На верхнее строение действует
центральная нагрузка
10000
кН.
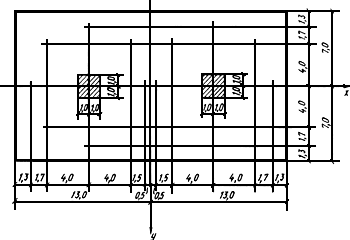
Рис.50. Плитный фундамент силосного корпуса
Характеристики материала
фундамента приняты равными: модуль
упругости бетона
26500000
кПа; толщина фундамента
1
м; коэффициент Пуассона бетона
0,167.
Для основания фундамента задан постоянный коэффициент жесткости (постели) 2470 кН/м .
Стойки высотой
12,8
м характеризуются осевой жесткостью
28350000
кПа·м
.
Расчет производим для
части фундамента (рис.51), учитывая
симметрию конструкции и заданной
нагрузки. Разбивка фундамента
конечно-элементной сеткой показана на
рис.51.
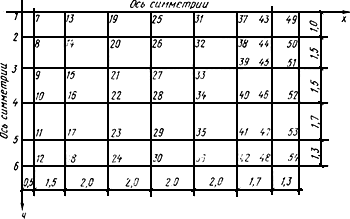
Рис.51. Схема разбивки плитного фундамента на конечные элементы
Расчет выполнен на ЭВМ
ЕС-1022 по программе КОРПУС-ЕС. Информация
к расчету описана на языке ВХОД (диалект
КОРПУС). В табл.75 приведены результаты
расчета в узлах 13-18
для двух вариантов загружений: 1 - нагрузка
приложена к плитному фундаменту; 2 -
нагрузка
приложена к силосному корпусу.
Таблица 75
#G0Узел сетки |
Координаты узлов сетки, м
|
Загружение |
Осадка , см |
Изгибающие моменты на 1 м сечения , кН·м/м
|
Крутящий момент на 1 м сечения , кН·м/м |
Отпор основания , кПа |
||
|
|
|
|
|
|
|
|
|
13
|
2,0 |
0,0 |
1 |
1,84 |
-343,0 |
184,4 |
3,5 |
45,5 |
|
|
|
2 |
1,12 |
-1,4 |
33,9 |
-3,4 |
27,7 |
14
|
2,0 |
1,0 |
1 |
1,83 |
-391,7 |
206,7 |
156,5 |
45,3 |
|
|
|
2 |
1,12 |
24,8 |
18,0 |
-34,8 |
27,7 |
15
|
2,0 |
2,5 |
1 |
1,80 |
-317,1 |
233,3 |
198,5 |
44,6 |
|
|
|
2 |
1,12 |
45,0 |
-21,2 |
-39,2 |
27,6 |
16
|
2,0 |
4,0 |
1 |
1,74 |
-201,1 |
173,9 |
145,5 |
43,1 |
|
|
|
2 |
1,11 |
92,3 |
90,6 |
-34,2 |
27,6 |
17
|
2,0 |
5,7 |
1 |
1,65 |
-163,6 |
36,4 |
77,8 |
40,8 |
|
|
|
2 |
1,11 |
6,6 |
-21,8 |
-25,2 |
27,5 |
18
|
2,0 |
7,0 |
1 |
1,57 |
-145,4 |
-6,7 |
46,5 |
38,9 |
|
|
|
2 |
1,10 |
-20,4 |
-1,9 |
-21,0 |
27,3 |