Расчет прямоугольных плитных фундаментов зданий со связевым каркасом при учете реактивных касательных напряжений

5.79. В рассматриваемой схеме связевого каркаса основными несущими элементами надфундаментного строения являются: система колонн (стоек), горизонтальные диски - перекрытия и диафрагмы жесткости.

5.80. Расчет плитного фундамента здания со связевым каркасом при учете реактивных касательных напряжений выполняют в следующей последовательности:

а) по существующему методу расчета, разработанному без учета реактивных касательных напряжений, определяют максимальные значения изгибающих моментов и прогибов плитного фундамента , ;

б) по рис.38 и 39 для заданных значений отношений толщины плиты к ее ширине или длине и модуля деформации основания к модулю деформации бетона плиты , находят значения коэффициентов и ;

в) расчетные значения изгибающих моментов и прогибов плитных фундаментов зданий со связевым каркасом при учете реактивных касательных напряжений определяют по формулам:

; (206)

, (207)

где , - определяются любым из практикуемых методов расчета плитных фундаментов, разработанных по пространственной схеме;

, - безразмерные коэффициенты перехода, с помощью которых учитывают влияние реактивных касательных напряжений.

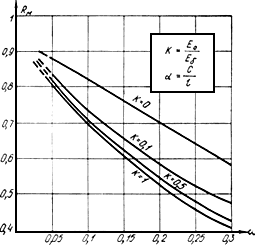
Рис.38. Коэффициент перехода

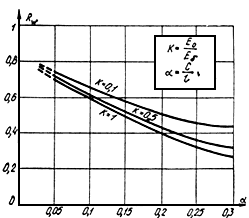
Рис.39. Коэффициент перехода

Пример расчета напряженно-деформированного состояния плитного фундамента

со связевым каркасом на упругом основании с учетом реактивных касательных напряжений

Для оценки влияния реактивных касательных напряжений на результаты расчета плитных фундаментов дается его расчет по методу, разработанному И.И.Гудушаури (с учетом реактивных касательных напряжений) и по методу П.И.Клубика, разработанного без учета этого фактора.

Рассматривают плитный фундамент, нагруженный равномерно распределенной нагрузкой с интенсивностью .

Расчет выполнен для частного случая, когда 0,1, где , - соответственно модули упругости основания и бетона плитного фундамента.

На рис.40 даются эпюры безразмерных величин прогибов и изгибающих моментов плитного фундамента, полученных с учетом и без учета влияний реактивных касательных напряжений.

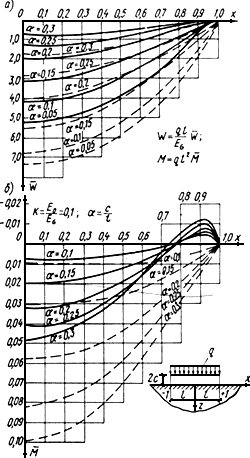
Рис.40. Результаты расчета плитного фундамента

с учетом реактивных касательных напряжений

а - эпюры прогибов при 0,1 и 0,05; 0,1; 0,15; 0,2; 0,25; 0,3

сплошные линии соответствуют 0, пунктирные - 0;

б - эпюры изгибающего моменты при 0,1 и 0,05; 0,1; 0,15; 0,2; 0,25; 0,3

Расчет толстых плитных фундаментов с учетом реактивных касательных напряжений

5.81. Расчет толстых плитных фундаментов выполняют на заданные внешние воздействия с целью определения толщины плиты и подбора арматуры (с их распределением в теле плитного фундамента) из условий прочности и деформаций. Такой расчет выполняют по теории упругости при точном удовлетворении всех граничных условий. По вертикальным граням плитного фундамента нормальные и касательные напряжения равны нулю. По верхней грани плитного фундамента касательные напряжения равны нулю, а нормальные напряжения равняются внешней нагрузке, если она распределенная, или же нулю, если она сосредоточенная. Если на плитный фундамент вертикальная нагрузка приложена в виде множества сосредоточенных сил, ее приводят к статически эквивалентной распределенной нагрузке. По подошве плитного фундамента нормальные и касательные перемещения соответствующих контактных точек плитного фундамента и основания (упругого полупространства) тождественно равны.

5.82. Для оценки погрешности расчета толстых плитных фундаментов, рассматриваемых как тонкие, следует использовать приведенные ниже указания.

5.83. Расчет толстых балочных плитных фундаментов при строгом удовлетворении всех граничных условий, указанных в п.5.81 (рис.41), а именно:

при

: ; ; (208)

при

: ; ; (209)

при

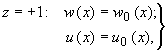(210)

выполняются по теории упругости при использовании метода наложения фиктивных ортотропных систем, разработанного И.И.Гудушаури. При этом в качестве модели основания принимают упругую полуплоскость с упругими характеристиками , , определяемыми согласно п.5.68.

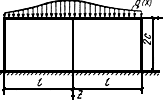
Рис.41. Схема расчета толстых плитных фундаментов

на упругом полупространстве в плоской постановке

5.84. Расчет толстых балочных плитных фундаментов (рис.41) с удовлетворением точно граничных условий (208)-(210) выполняют на ЭВМ по программе с шифром ТФП*. Она составлена на языках АЛГОЛ-60 и ФОРТРАН-IV.

_______________

* Шифр ТФП составлен из первых букв слов: толстый, фундамент и плита.

При расчете толстых плитных фундаментов (рис.41) по программе ТФП ЭВМ выдает результаты расчета в виде напряжений и перемещений для произвольного количества (заранее намеченного) точек:

а) безразмерные значения внутренних напряжений , , , действительные значения которых определяют из зависимостей:

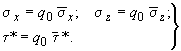(211)

б) безразмерные значения горизонтальных и вертикальных перемещений указанных точек плиты , , действительные значения которых определяют из зависимостей:

; (212)

, (213)

где ; - длина балочного плитного фундамента.

Пример расчета напряженно-деформированного состояния толстого плитного фундамента

на упругом полупространстве по теории упругости

(т.е. без гипотезы Бернулли) с учетом реактивных касательных напряжений

Расчет выполняют по пп.5.81-5.84. Задачу рассматривают в плоской постановке. В качестве модели основания принимается упругая полуплоскость. Приведенные ниже результаты численных примеров расчета плитных фундаментов получены для следующих характеристик:

24000 МПа - модуль упругости бетона;

0,17 - коэффициент Пуассона для бетона;

12000 МПа - модуль упругости основания.

На плитный фундамент действует равномерно распределенная нагрузка с интенсивностью .

Расчет выполнен по указаниям пп.5.81-5.84 на ЭВМ по программе ТФП для различных значений , где , - полуширина и полутолщина плитного фундамента.

На, рис.42, 43 даются сопоставления эпюр горизонтальных нормальных напряжений , полученных по теории упругости и с использованием гипотезы Бернулли при учете реактивных касательных напряжений.

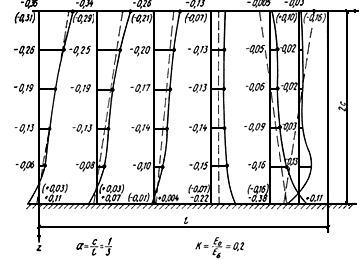
Рис.42. Сопоставление эпюр горизонтальных нормальных напряжений,

построенных для поперечных сечений плиты при ; 0,2;

сплошные линии соответствуют расчету по теории упругости, а пунктирные линии - расчету

с использованием гипотезы Бернулли при учете реактивных касательных напряжений

Рис.43. Сопоставление эпюр горизонтальных нормальных напряжений ,

построенных для поперечных сечений фундаментной плиты при 0,2; 1;

сплошные линии соответствуют расчету по теории упругости, а пунктирные линии - расчету

с использованием гипотезы Бернулли при учете реактивных касательных напряжений

На рис.44 даются сопоставления эпюр прогибов, полученные по трем различным методам: по теории упругости; при использовании гипотезы Бернулли, когда учитываются реактивные касательные напряжения; при использовании гипотезы Бернулли без учета реактивных касательных напряжений.

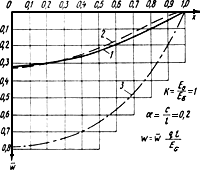
Рис.44. Сопоставление прогибов плитного фундамента,

полученных при 1; 0,2 по трем различным способам

1 - по теории упругости, т.е. без использования гипотезы Бернулли; 2 - при использовании

гипотезы Бернулли, но учитывая влияние реактивных касательных напряжений ;

3 - при использовании гипотезы Бернулли и принимая 0