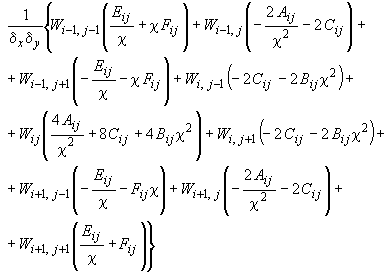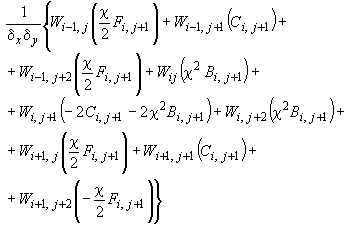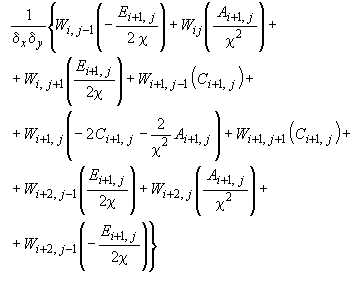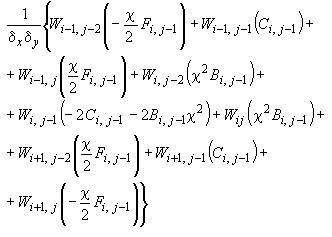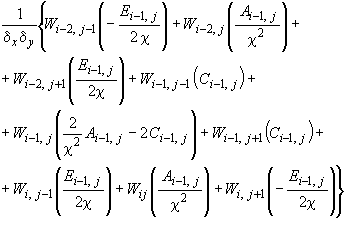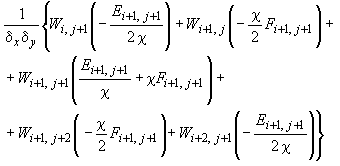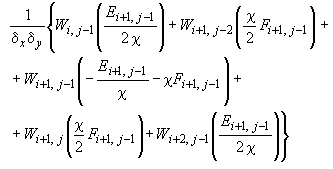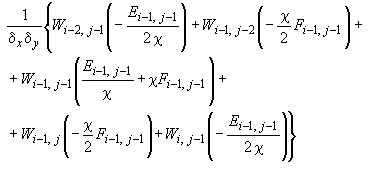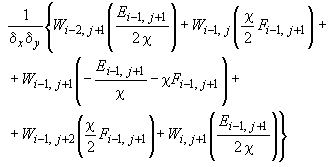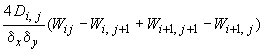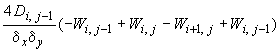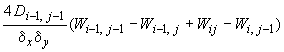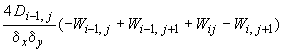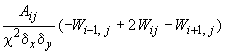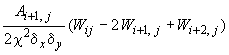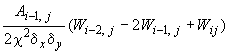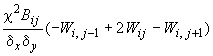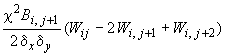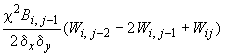Элементарные операторы для формирования разрешающих уравнений при расчете плиты с учетом особенностей деформирования железобетона

Таблица 66

#G0Тип оператора	Оператор
1. Для внутреннего центрального узла
2. Для внутреннего верхнего узла
3. Для внутреннего правого узла
4. Для внутреннего нижнего узла
5. Для внутреннего левого узла
6. Для внутреннего правого верхнего узла
7. Для внутреннего правого нижнего узла
8. Для внутреннего левого нижнего узла
9. Для внутреннего левого верхнего узла
10. Крутильный для верхней правой ячейки
11. Крутильный для нижней правой ячейки
12. Крутильный для нижней левой ячейки
13. Крутильный для верхней левой ячейки
14. Для центрального узла на горизонтальном краю
15. Для правого узла на горизонтальном краю
16. Для левого узла на горизонтальном краю
17. Для центрального узла на вертикальном краю
18. Для верхнего узла на вертикальном краю
19. Для нижнего узла на горизонтальном краю

В первых девяти операторах табл.66 не учитывается потенциальная энергия деформации изотропного кручения в связи с тем, что кривизна кручения для узлов разностной сетки записывается с точностью на порядок ниже, чем изгибные кривизны и . Для слагаемых, связанных с анизотропией, для одной и той же точки (узла разностной сетки) необходимо записать вторые однородную и смешанную производные. Кривизны изотропного кручения в целях повышения точности следует записывать для центров ячеек. Коэффициент жесткости в операторах 10-13 определяют как среднюю для углов рассматриваемой ячейки величину.

В шести последних операторах, приведенных в табл.66, обозначено:

(76)

При формировании уравнений (65) добавляют выражение (70) к элементу, стоящему на главной диагонали. Правая часть соотношения (68) представляет собой свободные члены уравнений (65).

Матрица системы уравнений получается ленточная симметричная. Ширина ленты равна 4 3, где - число узлов вдоль короткой стороны плиты. В каждой строке может быть 21 коэффициент, отличный от нуля.

5.24. Вычисление коэффициентов жесткости плиты как функций кривизны выполняется изложенным ниже способом. Записывают кривизны через моменты, пренебрегая мембранными усилиями:

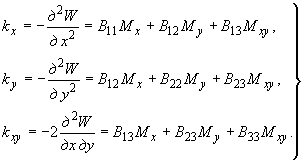(77)

Коэффициенты жесткости , , , , , выражают через податливости . Для этого из уравнения (77) находят моменты, записывают соответствующие тождества, используя соотношения (73) и (74), и получают:

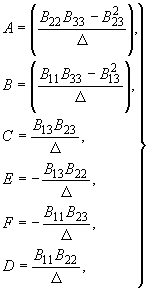(78)

.

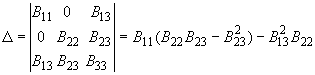В выражениях (78) коэффициент 0, так как с появлением трещин коэффициент поперечной деформации бетона становится равным нулю.

Различают следующие четыре стадии работы железобетона:

первая стадия соответствует упругой работе бетона;

вторая - упругопластической работе бетона до образования трещин в растянутой зоне;

третья - работе бетона с трещинами или упругой работе арматуры;

четвертая - работе арматуры в трещинах за пределом упругости.

В первой и второй стадиях железобетон рассматривается как изотропный материал и влияние арматуры не учитывается. При этом больший по абсолютной величине главный момент и момент трещинообразования связаны неравенством:

.

Момент трещинообразования определяется по формуле

. (79)

Максимальный по абсолютной величине главный момент находится по зависимости

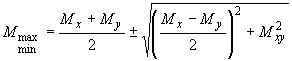. (80)

На первой стадии работы железобетона и коэффициенты жесткости в соотношениях (73) и (74) соответственно равны:

, , , . (81)

Здесь 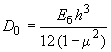- цилиндрическая жесткость плиты.

На второй стадии 0,5 и коэффициенты жесткости вычисляют по формулам (81) после замены на :

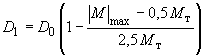. (82)

Величину можно записать непосредственно через кривизны, подставив в виде

. (83)

При этом - большая, а - меньшая по абсолютной величине главные кривизны, определяемые по формуле

. (84)

В результате получают

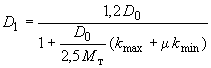. (85)

При (третья и четвертая стадии работы железобетона) в растянутой зоне бетона появляются трещины. Различают три основные схемы трещин в плите (рис.25):

непересекающиеся трещины в нижней (схема 1Н) или верхней (схема 1В) зоне;

пересекающиеся трещины в нижней (схема 2Н) или верхней (схема 2В) зоне;

непересекающиеся трещины в нижней и верхней зонах (схема 3).

Рис.25. Основные схемы трещин в плите

а - схема 1Н, а’ - схема 1В, б - схема 2Н, б’ - схема 2В, в - схема 3

Угол между ними и верхними трещинами считается равным .

Если трещины в точках плиты не были зафиксированы ранее, то установив, что , необходимо проверить условия

(86)

и

. (87)

Выполнение условия (86) говорит об образовании трещин по схеме 2Н. Справедливость соотношения (87) указывает на образование трещин по схеме 3. Если не выполняются условия (86) и (87), то в точке плиты образовались непересекающиеся трещины в нижней зоне. Угол наклона трещин к оси определяют по формуле

. (88)

Когда трещины в плите обнаружены, вместо условий (86) и (87) проверяются неравенства:

(89)

и

, (90)

где - момент вдоль трещины, равный:

. (91)

Выражения для коэффициентов при схеме трещин 1Н имеют вид:

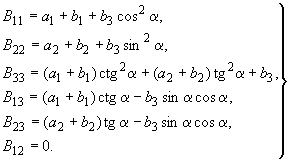(92)

В формулах (92) введены обозначения параметров, из которых формируются жесткостные коэффициенты при любой схеме трещин:

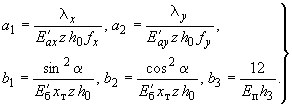(93)

Для получения в случае схемы трещин 1B в выражениях (92) следует заменить , , , и соответственно на , , , и , т.е. взять те же параметры (93), но подставлять в них данные не для нижнего, а для верхнего армирования.

В формулы (93) входит целый ряд переменных величин, определяемых по-разному в зависимости от стадии работы арматуры. Границами являются напряжения , (или ) и .

Высота сжатой зоны бетона над трещиной и плечи пар внутренних сил равны:

, , . (94)

Относительная высота сжатой зоны определяется по формуле

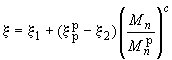, (95)

где - изгибающий момент в перпендикулярной трещине плоскости, равный:

. (96)

Предельная величина этого момента определяется как для балки с коэффициентом армирования

. (97)

Обобщенный коэффициент армирования перпендикулярно трещине равен:

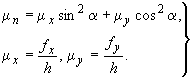(98)

Относительная высота сжатой зоны при текучести арматуры равна:

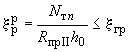, (99)

где вычисляется по формуле (30) СНиП II-21-75*.

______________

* Заменен на #M12293 0 871001190 3704477087 78 23943 2465715556 2685059051 3363248087 4294967268 584910322СНиП 2.03.01-84#S, здесь и далее. - Примечание изготовителя базы данных.

Проекция усилий текучести в арматуре на нормаль к трещине составляет

. (100)

Входящие в (95) величины и равны:

; , (101)

где

, , .

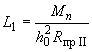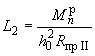Показатель степени "с" в выражении (95) равен 3, если

и 5 при .

Высота сжатой зоны бетона под верхними трещинами определяется по тем же формулам (95)-(101) с заменой величин , и на величины , , , соответствующие верхнему армированию.

Бетон сжатой зоны над (или под) трещинами деформируется как ортотропный материал, оси ортотропии которого параллельны и перпендикулярны направлению трещин.

Средний модуль деформации сжатого бетона в перпендикулярном трещине направлении определяется выражением

, (102)

в котором:

, , ,

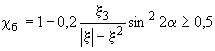, , (103)

.

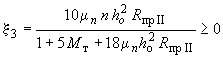Средний модуль деформации бетона под верхними трещинами получается из выражений (102)-(103) подстановкой величин , , , .

Деформативность полос бетона вдоль трещин характеризуется модулем , который приближенно можно вычислять по формуле

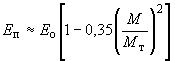, (104)

где - главный момент, минимальный по модулю из величин и .

Средний модуль деформации арматуры, параллельной оси , на любой стадии работы определяется формулой

, (105)

где

. (106)

Коэффициент определяется в зависимости от величины напряжений по следующим формулам:

; (107)

при

, (108)

где

, (109)

при

, (110)

. (111)

В формулах (109) и (111) напряжения берутся в МПа.

В формуле (105) величина определяется зависимостью

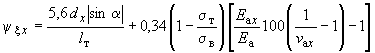. (112)

В формулу (112) входит расстояние между трещинами, принимаемое равным большей из двух величин

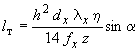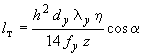и , (113)

где , - диаметр арматурных стержней вдоль осей и ; - коэффициент, принимаемый для арматурных стержней периодического профиля 0,7, для гладких горячекатаных стержней 1, для арматурной проволоки 1,25.

Средний модуль деформации арматуры, параллельной оси , определяется по формулам (105)-(112) с заменой индекса на . При этом в выражении (112) надо вместо взять .

Коэффициенты и учитывают влияние касательных напряжений в арматуре:

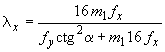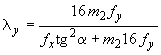, , (114)

где и - поправочные коэффициенты при упругопластической стадии работы арматуры (при упругой стадии работы арматуры коэффициенты и принимают равными 1).

В общем случае коэффициенты и определяют по соотношениям

и , (115)

где и - коэффициенты, определяемые по формулам (107)-(111) с заменой индекса на при нахождении коэффициента .

Для вычисления коэффициентов , , и необходимо знать величины напряжений в арматуре и (или и ), которые нужно найти через моменты последовательными приближениями

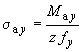и , (116)

где

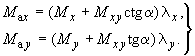(117)

Итеративный процесс нахождения и начинают с 1.

Жесткостные коэффициенты для третьей схемы трещин (пересекающиеся трещины в разных зонах плиты) получают суммированием соответствующих величин, вычисленных для схем 1Н и 1В:

. (118)

При этом в соотношениях (93) принимают равным нулю. Если трещины возникают по схеме 2Н или 2В (пересекающиеся трещины в нижней или верхней зонах), податливости равны:

, , . (119)

При вычислении слагаемых в и принимаются:

, , ,

, .

Жесткость на кручение при этой схеме трещин приближенно принимают равной:

, .

Это допущение не только вносит погрешность, но и связано с некоторыми неудобствами: видоизменяется матрица системы уравнений, определяющих прогибы (перемещения) плиты; исключается возможность использования соотношений (78) для перехода от податливостей к жесткостным коэффициентам , , , , и . Поэтому величина для второй схемы трещин определяется как 1000: .

Для любой схемы трещин вычисление податливостей выполняется по соотношениям, записанным для схемы трещин 1Н. Это достигается введением кроме действительного угла , определяющего направление трещины, и заданного армирования вспомогательных углов , и и расчетного армирования . В зависимости от схемы трещин каждой из этих величин присваивается значение согласно табл.67. Для схемы трещин 3 вычисление осуществляется сначала как для схемы 1Н ( 5), затем как для схемы 1В при ( 6) с последующим суммированием.

Таблица 67

#G0Тип схемы трещин	Значения признака типа схемы трещин	Вспомогательные углы			Расчетное армирование
1H	1
1В	2
1H	3		0
2B	4		0
3	5
	6

Угол наклона трещины к оси во всех случаях определяется по формуле (88). Если образовалась верхняя трещина (схема 1B, 2), вносится поправка на , так как положение трещины в этом случае определяется не , а . Найденная величина , соответствующая моменту появления трещины, в дальнейшем сохраняется независимо от положения главных площадок тензора моментов. Значение по абсолютной величине ограничивается в пределах от 0,01 до 1,56 радиана.

Признак схемы трещин может изменяться лишь в сторону добавления трещин в узле: к непересекающимся трещинам на нижней или верхней поверхности плиты могут добавиться пересекающие их трещины в той же или противоположной зоне.

Суть итеративного процесса, посредством которого определяются жесткостные коэффициенты при наличии трещин в узле, показана на рис.26. Пусть известны моменты , соответствующие кривизнам в данной точке на предыдущем этапе расчета плиты. Эти величины фиксируются в качестве координат начального полюса , . Пропорционально приращению кривизн , где - заданные кривизны, принимается приращение расчетных моментов . Максимальное приращение моментов ограничивается величиной, составляющей до 10% от соответствующего . По этим моментам вычисляются податливости и кривизны (точка 1 на рис.26). Новые значения расчетных моментов определяются соотношением

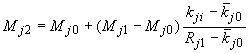, . (120)

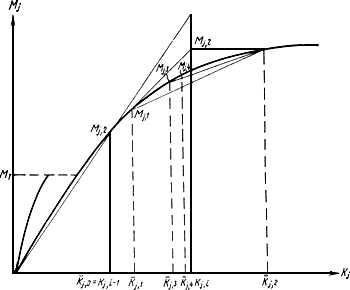
Рис.26. Принципы итеративного процесса определения жесткостных коэффициентов

при наличии трещин в узле разностной сетки

- моменты ( ; 0, 1, 2, ...) - кривизны.

Предварительно расчетные кривизны сравниваются с заданными кривизнами. Если разница между ними лежит в пределах требуемой точности, то соответствующий момент принимается равным .

Рассматривая точку 1 как полюс, по моментам вычисляют новые расчетные кривизны . По соотношению, аналогичному (120), находятся новые расчетные моменты . Для этого в формуле (120) вторые индексы всех ее членов, кроме , следует увеличить на единицу. Вычисляются новые расчетные кривизны . С использованием теперь в качестве полюса точки 2 по той же формуле (120) с заменой индексов находятся новые расчетные моменты и вычисляются расчетные кривизны и т.д. Процесс "микроитерации" продолжается до достижения требуемой точности по кривизнам.

5.25. Алгоритм расчета плиты составляется по указаниям пп.5.17-5.24. После ввода и обработки исходных данных выполняется линейный расчет; по полученным результатам формируется начальный параметр нагрузки , соответствующий по линейному решению моменту трещинообразования в наиболее нагруженной точке плиты; умножением на этот параметр производится пропорциональный пересчет прогибов, формируется признак линейного этапа расчета и начинается итеративный процесс решения нелинейной задачи.

Одна итерация состоит из следующих операций:

1) вычисление в каждом узле конечно-разностной сетки коэффициентов жесткости плиты по кривизнам, полученным в предыдущей итерации. В первой на каждом шаге нагружения итерации расчетные кривизны принимаются увеличенными в раз. (Здесь - параметр нагрузки на рассматриваемом -том шаге нагружения, - на предыдущем шаге). В узлах, лежащих на контуре, кривизны вычисляются с учетом граничных условий;

2) формирование и решение системы разрешающих уравнений. Для сокращения числа обращений к внешним запоминающим устройствам при большом числе узлов разностной сетки уравнения формируются блоками, каждый из которых соответствует одному ряду узлов по короткой стороне плиты. По мере формирования и обработки по схеме "прямого хода" блоки уравнений записываются на диски (при использовании ЭВМ серии ЕС). После формирования всех уравнений выполняется "обратный ход". Автоматизированное формирование матрицы разрешающих уравнений позволяет уменьшить число типов узлов для прямоугольной плиты с 25 до 9;

3) после анализа признака этапа расчета, показавшего что выполняется очередная итерация нелинейного расчета, необходимо перейти к оценке достигнутой точности решения по прогибам. Приращение перемещений в любом узле должно быть меньше заданной доли максимального прогиба, соответствующего начальному параметру нагрузки , умноженной на шаг приращения параметра нагрузки . Если точность недостаточная, то выполняется следующая итерация. При достижении требуемой точности увеличивается параметр нагрузки

. (121)

Расчет завершается при достижении заданной нагрузки.

5.26. Учет нелинейности деформирования железобетона позволяет увеличить, как правило, допустимую нагрузку на плиту за счет перераспределения и уменьшения максимальных значений усилий, но при этом обнаруживается резкое возрастание неравномерности осадок. Данные нелинейного расчета позволяют выполнить достоверную оценку работы конструкции по предельным состояниям второй группы. Для определения ширины раскрытия трещин используют формулу

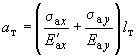. (122)

Параметры, входящие в формулу (122), вычисляют по формулам (105), (113), (116).

5.27. Изложенный выше алгоритм реализован в программе НРП-1 для ЭВМ серии ЕС. Программа составлена на алгоритмическом языке FORTRAN. Позволяет рассчитывать плитные фундаменты с произвольно заданной переменной толщиной и переменным армированием. При использовании в качестве внешних запоминающих устройств магнитных дисков число узлов разностной сетки при расчете плиты может достигать 2000.

Пример.

Размеры плиты и ее загружение показаны на рис.27. При расчете приняты:

бетон марки М 350;

арматура класса А-III горячекатаная;

процент армирования для верхней арматуры в обоих направлениях 0,2; для нижней 0,5;

диаметр нижней арматуры 20 мм, верхней 10 мм;

защитный слой бетона для нижней и верхней арматуры 3 см;

коэффициент жесткости основания 8 МН/м .

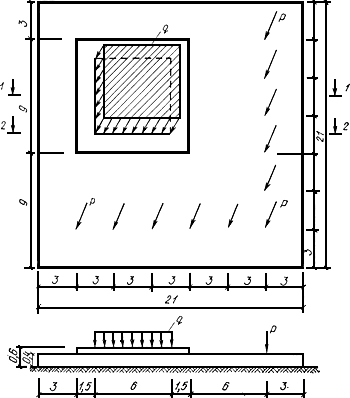
Рис.27. Схема плитного фундамента

На рис.28 и 29 приведены эпюры прогибов, изгибающих и крутящих моментов в сечениях 1-1, 2-2, соответствующие нагрузкам 0,16 МН/м и 1,1 МН. Максимальное раскрытие трещин при этом равно 0,41 мм. Нагрузка трещинообразования, определенная из линейного решения, составляет от расчетной 29,3%.

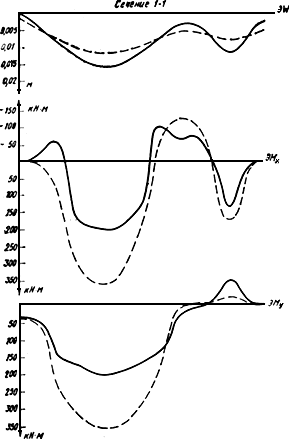
Рис.28. Перемещения и моменты в сечении 1-1

( - линейное решение, - нелинейное решение)

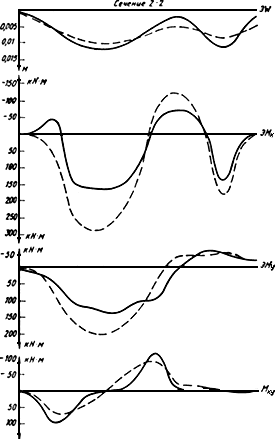
Рис.29. Перемещения и моменты в сечении 2-2

( - линейное решение, - нелинейное решение)

Анализ результатов показывает, что учет нелинейности деформирования железобетона выявляет существенное перераспределение усилий в сторону уменьшения пиков и увеличения неравномерности осадок.