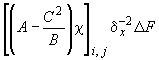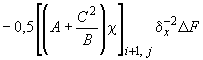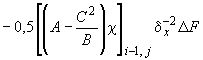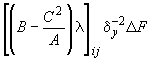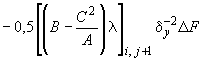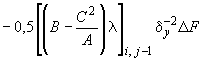Элементарные операторы для формирования уравнений (62)

#G0Тип элементарного оператора	Элементарный оператор
1. Изгибный для внутреннего центрального узла
2. Изгибный для внутреннего верхнего узла
3. Изгибный для внутреннего узла справа
4. Изгибный для внутреннего нижнего узла
5. Изгибный для внутреннего узла слева
6. Крутильный для верхней ячейки справа
7. Крутильный для нижней ячейки справа
8. Крутильный для нижней ячейки слева
9. Крутильный для верхней ячейки слева
10. Изгибный для центрального узла на горизонтальном краю
11. Изгибный для узла справа на горизонтальном краю
12. Изгибный для узла слева на горизонтальном краю
13. Изгибный для центрального узла на вертикальном краю
14. Изгибный для верхнего узла на вертикальном краю
15. Изгибный для нижнего узла на вертикальном краю

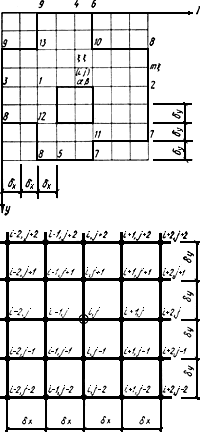
Рис.18. Типы узлов конечно-разностной сетки для плит произвольной формы в плане

После решения системы линейных алгебраических уравнений получают величины прогибов для всех узлов сетки.

Для определения величин изгибающих и крутящих моментов, действующих в сечениях плиты, используют выражения (58).

Реакции основания определяют по формуле

, (63)

где - реакция основания для -го узла сетки; - коэффициент жесткости основания в -ом узле; - прогиб плиты в -ом узле.

5.12. При подготовке расчетной схемы перемещения плиты в точках расположения жестких опор принимаются равными нулю:

.

При известной величине осадки свай в точках расположения свай задается коэффициент жесткости основания, определяемый по формуле

, (64)

где - средняя величина нагрузки на плиту; - осадка опоры.

5.13. Для расчета плит с учетом влияния жесткости надфундаментного строения следует использовать метод сил.

При этом принимают следующие предпосылки:

надфундаментное строение состоит из системы абсолютно жестких в своей плоскости диафрагм, расположенных параллельно координатам;

все диафрагмы связаны между собой абсолютно жесткими в горизонтальной плоскости связями, роль которых в реальной конструкции играют диски перекрытий;

от диафрагм на плиту передаются только вертикальные усилия, равные соответствующей внешней нагрузке, и моменты, величина которых определяется в результате расчета;

углы наклона диафрагм одного направления одинаковы, закручивание здания при этом не учитывается;

влияние горизонтальных усилий взаимодействия между плитой и диафрагмой не учитывается;

колонны передают на плиту только вертикальную нагрузку;

жесткость колонн не учитывается.

Окончательные результаты расчета плиты получаются суммированием величин, получаемых от действия внешних нагрузок и от моментов взаимодействия плиты с диафрагмами.

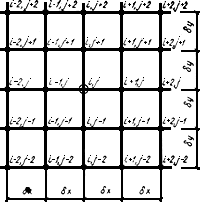
Рис.19. Расчетная схема плиты при учете совместной работы с надфундаментным строением

5.14. Для расчета плиты любой формы в плане следует принимать прямоугольную в плане разностную сетку, в которую вписывают рассчитываемую плиту. Сетка может быть как с квадратными, так и с прямоугольными ячейками. Шаг сетки в одном направлении принимается одинаковым. Число узлов сетки должно быть минимальным, но достаточным для характеристики деформации плиты и внутренних усилий, возникающих в ее сечениях. Оптимальным считается шаг, при котором размеры ячейки сетки соответствуют размерам площади на срединной поверхности плиты, воспринимающей нагрузку от несущего элемента верхнего строения.

Приближенно величину шага сетки определяют по формуле

,

где - шаг сетки; - минимальная ширина элемента, передающего нагрузку на плиту; - толщина плиты.

5.15. Точки приложения сосредоточенных нагрузок и центры тяжести площадок нагружения нужно совмещать с ближайшими узлами сетки.

5.16. Оси элементов надфундаментного строения (диафрагм, стен) должны совпадать с линиями сетки, для чего допускается некоторое смещение осей элементов от проектного положения.

Толщина стены приближенно принимается кратной шагу сетки. В этом случае ось стены или диафрагмы может не совпадать с линией сетки (рис.20). Диафрагмы, связанные между собой, не должны иметь толщину больше, чем величина 1-го шага сетки.

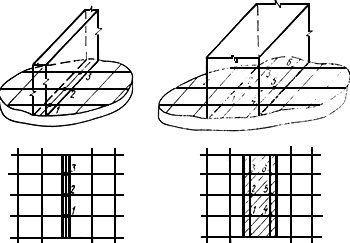
Рис.20. Схематизация диафрагм при расчете плиты по программе ПОРТИК

Пример. Рассмотрим фундаментную плиту произвольной ортогональной конфигурации (рис.21). Размеры прямоугольника, в который вписывается данная плита, равны 39х24 м. Основная толщина плиты 1,5 м. Ребра жесткости имеют высоту 1 м. Марка бетона 200. Модуль упругости бетона 2,4·10 кПа. Коэффициент Пуассона 0,2. Плита загружена системой сосредоточенных сил, приложенных в узлах сетки, принятой для расчета. Суммарная нагрузка на плиту 307,8 МН. Шаг сетки в обоих направлениях равен 1,5 м. В одном из расчетов в качестве основания принята модель с переменным коэффициентом жесткости. Схема распределения коэффициентов жесткости, МН/м , по площади плиты и их величины показана на рис.22. В другом расчете основание было однородным с коэффициентом постели, равным 1,75 МН/м . Результаты обоих расчетов приведены на рис.23. Эпюры изгибающих моментов показаны для сечений 1-1 и 2-2.

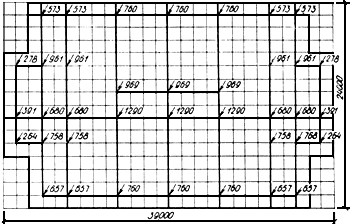
Рис.21. Схема плитного фундамента, рассчитанного

на однородном и неоднородном основании

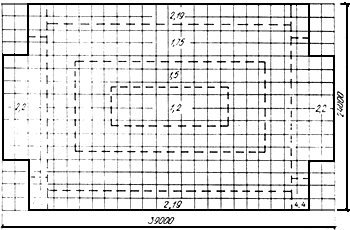
Рис.22. Схема распределения коэффициентов жесткости основания в плане плиты

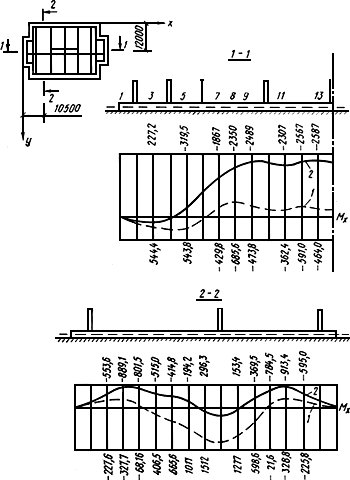
Рис.23. Сопоставление результатов расчетов плиты

на неоднородном и однородном основаниях

1 - неоднородное основание; 2 - однородное основание