3.3. Расчет гидравлических характеристик схемы

Расчет включает выбор базовой ветви трубопровода, расчет требуемой производительности и напора насоса.

Расчет гидравлических параметров схемы необходим для определения затрат энергии на перемещение жидкости и подбора стандартной гидравлической машины (насоса).

Заданная технологическая схема содержит емкости, расположенные на различных отметках высот, центробежный насос и сложный разветвленный трубопровод с установленной на нем запорной и регулирующей арматурой, включающий ряд местных сопротивлений. Расчет целесообразно начинать с определения диаметров трубопровода по формуле

. (3.4)

Так как расход среды Q_i известен, для расчета диаметра необходимо задаться значением скорости w. Чем больше скорость, тем меньше требуемый диаметр трубопровода, т.е. меньше стоимость трубопровода. Но с увеличением скорости растут потери напора в трубопроводе, что приводит к увеличению затрат энергии на перемещение жидкости. На практике для сред, перекачиваемых насосами, рекомендуют принимать значение экономической скорости w  1,5 м/с.

На основании рассчитанных значений d_i выбирается ближайший стандартный диаметр трубы d_{ст i} по ГОСТ 3262–75 для стальных водогазопроводных труб [1]. Краткая выписка из ука­занного ГОСТа приведена в прил.В.

В случае значительных диаметров, выходящих за пределы диапазона размеров труб, установленных ГОСТ 3262–75, могут использоваться ГОСТ 8734–78 [2] или ГОСТ 8732–78 [3] (прил. Г, Д).

Так как внутренние диаметры стандартных труб могут отличаться от значений, рассчитанных по формуле (3.4), необходимо уточнить скорость течения жидкости:

. (3.5)

Далее определяем потери напора в трубопроводе. Потери напора разделяют на потери на трение по длине и местные потери. Потери на трение возникают в прямых трубах постоянного сечения и возникают пропорционально длине трубы. Они определяются по формуле

. (3.6)

Безразмерный коэффициент потерь на трение по длине (коэф­фициент Дарси) можно рассчитать по универсальной формуле А.Д. Альтшуля [4,5]:

, (3.7)

где Δ_i – абсолютная эквивалентная шероховатость, завися­щая от состояния труб.

Значения абсолютной шероховатости труб приведены в табл. 2.

Таблица 2. Ориентировочные значения абсолютной шероховатости труб, Δ

Трубы	Δ, мм
Стальные новые Стальные, бывшие в эксплуатация с незначительной коррозией Стальные старые, загрязненные Чугунные новые, керамические Чугунные водопроводные, бывшие в эксплуатации Алюминиевые гладкие Трубы из латуни, меди и свинца	0,06 – 0,1 0,1 – 0,2 0,5 – 2 0,35 – 1 1,4 0,015 – 0,06 0,0015 – 0,01

Местные потери обусловлены местными гидравлическими сопротивлениями, т. е. местными изменениями формы и размера русла, вызывающими деформацию потока. К ним относятся: резкие повороты трубы (колена), плавные повороты, входы и выходы из трубопроводов, резкие (внезапные) расширения и сужения, конфузоры, диффузоры, теплообменники, вентили и т. д.

Местные потери напора определяются по формуле Вейсбаха следующим образом:

. (3.8)

Коэффициенты сопротивления ξ для ряда видов местных сопротивлений приведены в прил. Е.

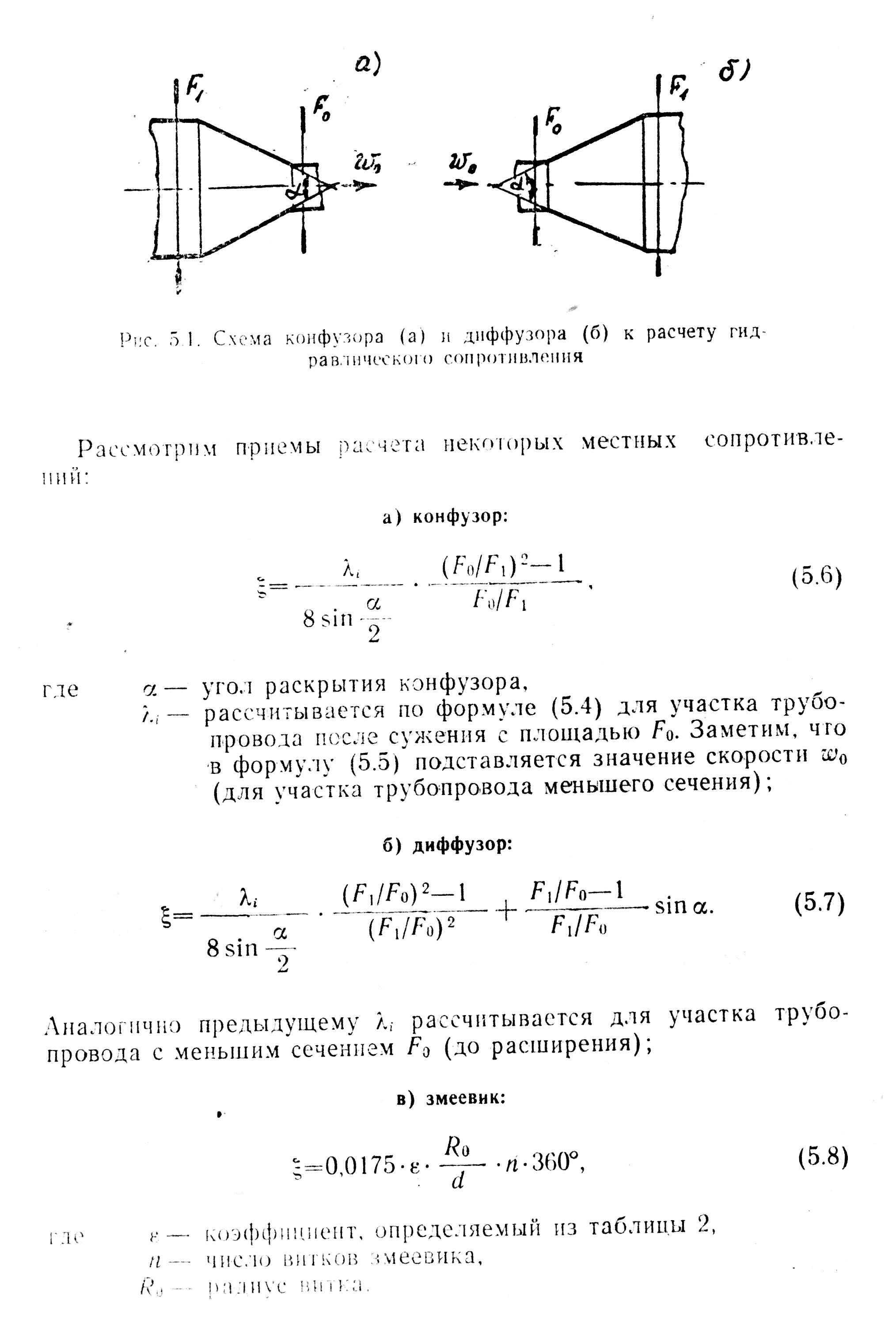
Рис. 3.3 Схема конфузора (а) и диффузора (б) к расчету гид­равлического сопротивления

Рассмотрим приемы расчета некоторых местных сопротивле­ний.

Коэффициент местного сопротивления конфузора (рис. 3.3, а) рассчитывается по формуле

, (3.9)

где α – угол раскрытия конфузора; λ_i – рассчитывается по формуле (3.7) для участка трубопровода после сужения с площадью F₀. Заметим, что в формулу (3.8) подставляется значение скорости w₀ (для участка трубопровода меньшего сечения).

Коэффициент местного сопротивления диффузора (рис. 3.3, б) рассчитывается по формуле

. (3.10)

Аналогично предыдущему λ_i рассчитывается для участка трубопровода с меньшим сечением F₀ (до расширения).

Коэффициент местного сопротивления змеевика (рис. 3.4) рассчитывается по формуле:

, (3.11)

где ε – коэффициент, определяемый из табл. 3; п – число витков змеевика, R₀ – радиус витка.

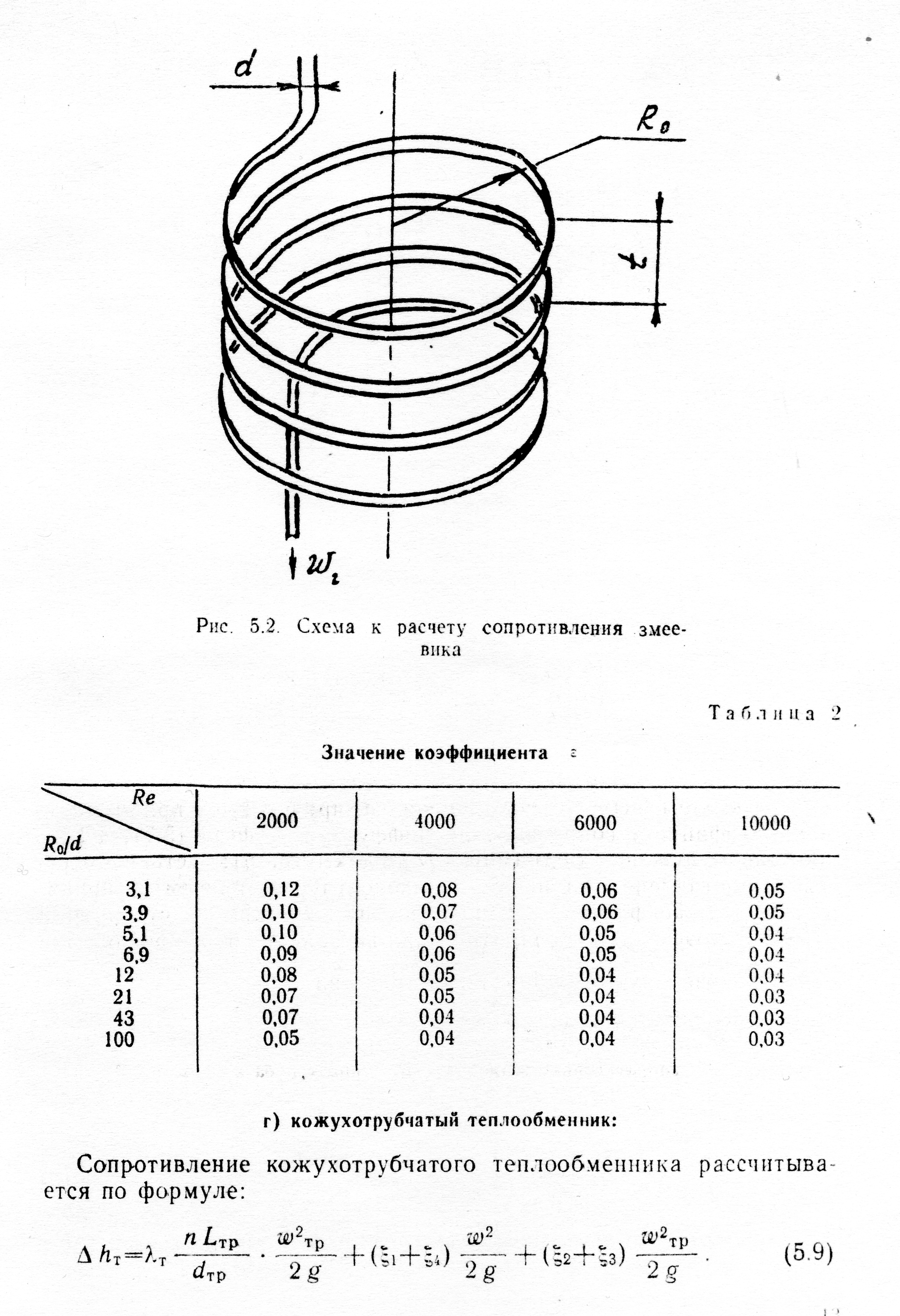
Рис. 3.4 Схема к расчету сопротивления змее­вика

Таблица 3. Значение коэффициента

Re R0 /d	2000	4000	6000	10000
3,1	0,12	0,08	0,06	0,05
3,9	0,10	0,07	0,06	0,05
5,1	0,10	0,06	0,05	0,04
6,9	0,09	0,06	0,05	0,04
12	0,08	0,05	0,04	0,04
21	0,07	0,05	0,04	0,03
43	0,07	0,04	0,04	0,03
100	0,05	0,04	0,04	0,03

Сопротивление кожухотрубчатого теплообменника (рис. 3.5) рассчитыва­ется по формуле

. (3.12)

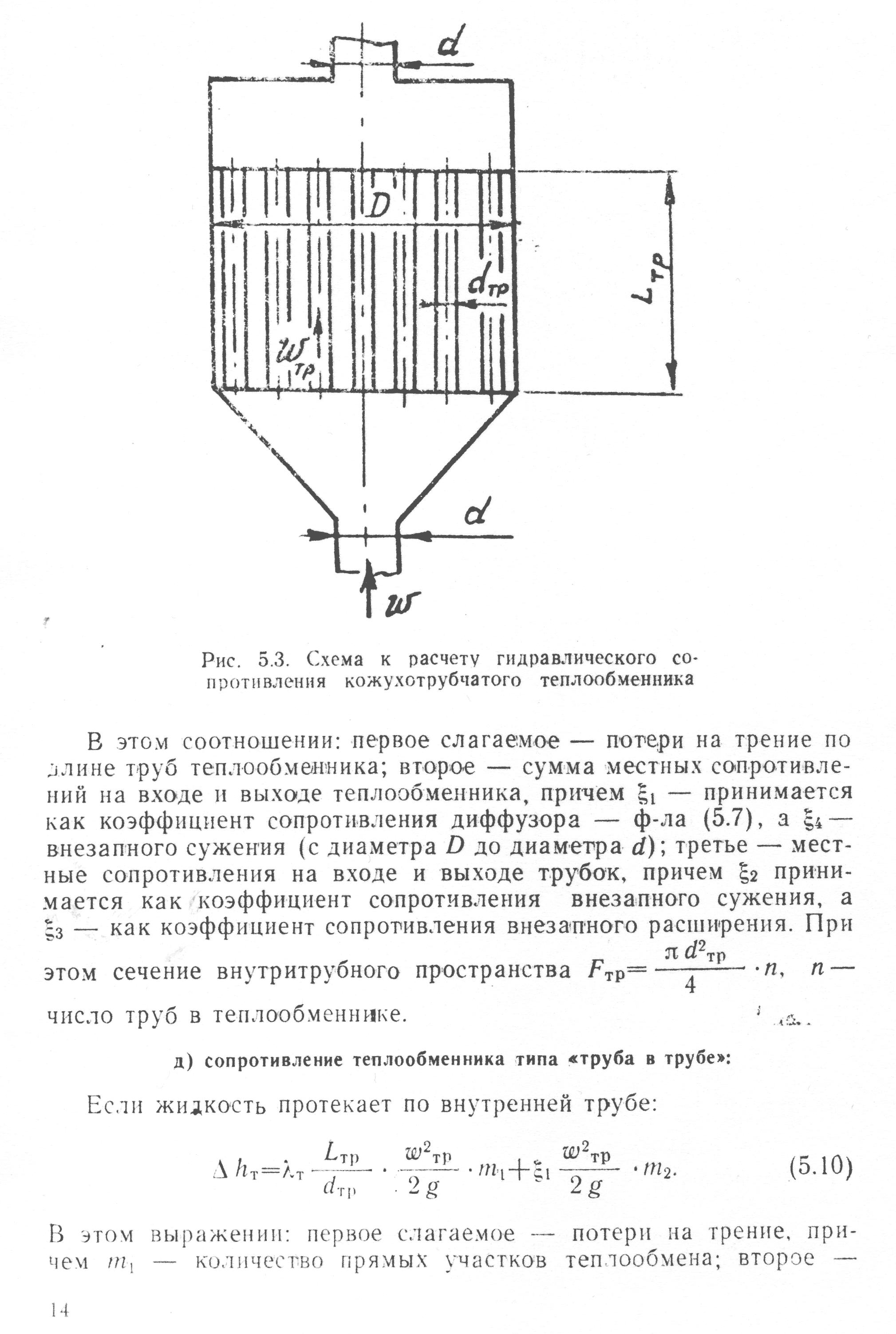
Рис. 3.5 Схема к расчету гидравлического сопротивления кожухотрубчатого