Глава 21. Измерение результативности торговли 739

воположность арифметическому) при расчете средней месячной доход­ности, которую затем выражают в процентах годовых, чтобы получить числитель коэффициента Шарпа. Средняя геометрическая доходность в процентах годовых в точности эквивалентна средней годовой доход­ности с учетом реинвестиций, которая обсуждается позже в этой главе в разделе, посвященном отношению прибыли к максимальному падению стоимости активов.

2. Коэффициент Шарпа не делает различий между коле­- баниями стоимости активов вверх и вниз. Коэффициент Шарпа измеряет волатильность, а не риск. А это не обязательно одно и то же.

С точки зрения меры риска, используемой в коэффициенте Шар­па, т.е. стандартного отклонения доходности, колебания вверх и вниз рассматриваются как в равной степени плохие. Таким образом, коэф­фициент Шарпа показывал бы в невыгодном свете управляющего, у которого спорадически наблюдались бы резкие увеличения активов, даже если бы падения стоимости активов были малы.

Рис. 21.3 сравнивает гипотетическое движение активов менедже­ра С, где время от времени наблюдается рост активов и отсутствует их падения, и менеджера D, который столкнулся с несколькими падения­ми стоимости активов. Хотя оба управляющих зафиксировали равную прибыль за период в целом, и менеджер D столкнулся с несколькими отрицательными переоценками, в то время как у менеджера С их не было, коэффициент Шарпа оценил бы менеджера D выше (см. табли­цу). Такой исход — прямое следствие того факта, что коэффициент Шарпа оценивает верхнюю волатильность точно так же, как и нижнюю.

3. Коэффициент Шарпа не делает различий между череду­- ющимися и последовательными убытками. Мера риска в коэф­- фициенте Шарпа (стандартное отклонение) не зависит от последова­- тельности выигрышных и убыточных периодов.

На рис. 21.4 показано гипотетическое изменение стоимости акти­вов с начальной величиной $100 000, управляемых менеджером Е и менеджером F. Каждый из них в обшей сложности зарабатывает $48 000, или $24 000 в год. Однако у менеджера Е месячные доходы в $8000 чередуются с месячными потерями в размере $4000, в то вре­мя как менеджер F сразу теряет $48 000 в первые 12 месяцев и пос­ледовательно зарабатывает $96 000 в течение оставшегося периода.

Коэффициент Шарпа этих двух управляющих был бы одним и тем же. Несмотря на этот факт, мало нашлось бы трейдеров, рассматри­вающих деятельность этих менеджеров как эквивалентную с точки зре­ния риска. Фактически все трейдеры согласились бы с тем, что резуль­таты менеджера F подразумевают значительно более высокий уровень риска.

740

Рисунок 21.3.

СРАВНЕНИЕ УПРАВЛЯЮЩЕГО С ВЫСОКОЙ ВОЛАТИЛЬНОСТЬЮ, ВЫЗВАННОЙ РЕЗКИМ РОСТОМ АКТИВОВ

ПРИ ОТСУТСТВИИ ПАДЕНИЯ СТОИМОСТИ АКТИВОВ, И УПРАВЛЯЮЩЕГО С ПАДЕНИЯМИ СТОИМОСТИ АКТИВОВ

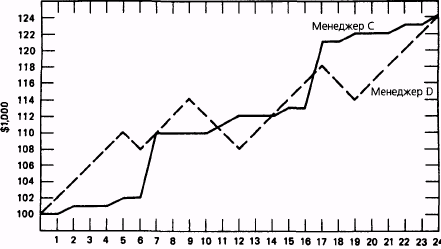
Рисунок 21 Л.

СРАВНЕНИЕ ДВУХ УПРАВЛЯЮЩИХ С ОДИНАКОВОЙ

ДОХОДНОСТЬЮ И СТАНДАРТНЫМ ОТКЛОНЕНИЕМ, НО С

РАЗЛИЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ МЕСЯЧНЫХ

ПРИБЫЛЕЙ И УБЫТКОВ

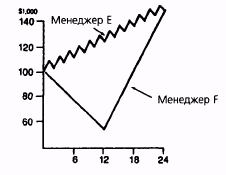
Источник: Дж. Швагер «Alternative to Sharpe Ratio Better Measure of Performance», Futures, p. 56, March 1985.

Таблица 21.1.

СРАВНЕНИЕ ЕЖЕМЕСЯЧНЫХ ПРИБЫЛЕЙ ДВУХ УПРАВЛЯЮЩИХ

741

Месяц	Менеджер С Изменение Совокупное активов изменение активов		Менеджер D Изменение Совокупное активов изменение активов
1	0	0	2000	2000
2	1000	1000	2000	4000
3	0	1000	2000	6000
4	0	1000	2000	8000
5	1000	2000	2000	10000
6	0	2000	-2000	8000
7	8000	10000	2000	10000
8	0	10000	2000	12000
9	0	10000	2000	14000
10	0	10000	-2000	12000
11	1000	11000	-2000	10000
12	1000	12000	-2000	8000
13	0	12000	2000	10000
14	0	12000	2000	12000
15	1000	13000	2000	14000
16	0	13000	2000	16000
17	8000	21000	2000	18000
18	0	21000	-2000	16000
19	1000	22000	-2000	14000
20	0	22000	2000	16000
21	0	22000	2000	18000
22	1000	23000	2000	20000
23	0	23000	2000	22000
24	1000	24000	2000	24000

Средняя месячная прибыль = 1000

Средняя месячная прибыль = 1000

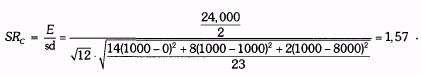
742 ЧАСТЬ 4. торговые системы и измерение эффективности торговли Таблица 21.1. (продолжение)

ОТНОШЕНИЕ ПРИБЫЛИ К МАКСИМАЛЬНОМУ ПАДЕНИЮ СТОИМОСТИ АКТИВОВ (RETURN RETRACEMENT RATIO — RRR)

RRR предлагает меру соотношения доходности и риска, которая позво­ляет избежать недостатков коэффициента Шарпа, обсуждавшихся в предыдущем разделе. Кроме того, RRR ближе к восприятию риска боль­шинством трейдеров. RRR представляет собой среднюю прибыль с уче­том реинвестирования (R), пересчитанную в годовом исчислении и де­ленную на усредненное за год максимальное снижение стоимости ак­тивов (average maximum retracement measure — AMR):