Постановка завдання оптимізації

У завданнях оптимізації потрібно знайти значення параметрів або функцій, що реалізовують максимум або мінімум деякої залежної від них величини, наприклад:

z=f(x₁, x₂,...,x_n), (4)

часто при додаткових умовах-нерівностях:

_i(x₁, x₂, …, x_m)< 0 (i=1, 2, ...,т). (5)

У багатьох інженерних і економічних завданнях, наприклад, бажано знайти максимум міри виконання або мінімум вартості.

Іншим додатком завдань оптимізації є здобуття наближених рішень вибором невідомих значень параметрів або функцій так, щоб вони давали мінімум помилки.

У простому випадку однієї незалежної змінної х локальні максимум і мінімум функції визначаються таким чином. Дійсна функція f(x), визначена при х = а, має в крапці а (локальний) мінімум або (локальний) максимум f(a), якщо існує таке позитивне число (, що при всіх (x = х - а, для яких виконуються нерівності 0 < | x | < ( і існує значення f(а +(x), відповідно

f  f(a + x) - f(а) < 0

або

f  f(а + x) - f(а) > 0.

Максимум і мінімум функції об'єднуються загальною назвою екстремуму функції. Визначення локальний підкреслює той факт, що поняття екстремуму пов'язане лише з досить малою околицею крапки а. При вирішенні оптимізаціонних завдань важливе знаходження не локальних екстремумів, а глобального максимуму або глобального мінімуму (найбільшого або найменшого значень) функції на проміжку X.

Для пошуку екстремумів існують різні методи. Часто трапляється, що при відшуканні максимумів і мінімумів функцій багатьох змінних отримують складну систему рівнянь, в цих випадках екстремуми знаходяться чисельними методами, тобто за допомогою послідовного вживання методу проб. При цьому вживання комп'ютера є практично єдиним способом рішення завдання.

Розв’язання рівнянь з одним невідомим

Одним з додатків завдань оптимізації є чисельне вирішення систем рівнянь з одним або декількома невідомими вигляду:

f(x) = 0. (6)

Знаходження коріння рівняння вигляду (6) навіть в разі алгебри рівнянь вище за третю міру представляє досить складне завдання. Трансцен­дентне з рівнянь найчастіше взагалі не мають аналітичного рішення. У цих випадках єдиним дорогою є здобуття наближених рішень, вибо­ру невідомих значень параметрів так, щоб вони давали мінімум помилки деякої цільової функції (як правило, квадратичною). Зазвичай використовуються ітераційні методи, коли спочатку вибирають деяке початкове наближення x^[0] потім обчислюють послідовні наближення

x ^{[j+ 1]} =  (x^[j]) (j = 0, 1,2,...).

Ітераційні методи забезпечують збіжність таких наближень до шуканого значення x:

У MS Excel для вирішення рівнянь вигляду (6) використовується зручний і простий для розуміння інструмент Підбір параметра. Він реалізує алгоритм чисельного вирішення рівняння, залежного від однієї змінної.

Процес рішення за допомогою процедури Підбір параметра розпадається на два етапи:

1. Завдання на робочому аркуші клітини, що містить змінну рівняння, що розв’язується (так званого впливаючої клітини), і клітини що містить формулу рівняння (залежного або цільової клітини).

2. Введення адрес впливаючої і цільової клітини в діалоговому вікні Підбір параметра і здобуття відповіді (або повідомлення про його відсутність або неможливість знайдення, оскільки рівняння може не мати рішень або алгоритм рішення (оптимізації) може виявитися таким, що розходиться в конкретних умовах).

На жаль, за допомогою процедури Підбір параметра можуть бути вирішені лише деякі типи рівнянь.

Приклад

Знайти рішення рівняння lп х = 0.

Рішення:

Перший етап

1. Відкриваємо новий робочий аркуш (команда Вставка > Аркуш).

2. Заносимо у клітину А1 орієнтовне значення кореня, наприклад, 3.

3. Заносимо у клітину В1 ліву частину рівняння, використовуючи як незалежну змінну заслання на клітину А1. Для цього натискуємо на панелі інструментів Стандартна кнопку Вставку функції; у діалоговому вікні, що з'явилося, Майстер функцій в робочому полі Категорія вибираємо Математичні, а в робочому полі Функція ім'я функції LN. Після чого клацаємо на кнопці 0К; діалогове вікно LN, що з'явилося, мишею відсовуємо убік від вічка А1 і в робоче поле Число клацанням миші на клітину А1 вводимо її адресу. Після чого натискуємо на кнопку ОК.

У клітину В1 з'являється число 1,098612.

Другий етап

1. Викликаємо процедуру Підбір параметра (команда Сервіс > Підбір параметра).

2. У полі Встановити у клітину мишею вказуємо В1, в полі Значення з клавіатури задаємо 0 (права частина рівняння), в полі Змінюючи значення вічка мишею вказуємо А1 (рис. 1).

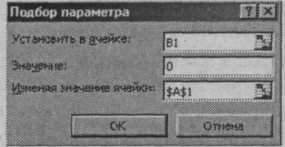
Рис. 1. Приклад заповнення діалогового вікна Підбір параметра

3. Клацаємо на кнопці 0К і отримуємо результат підбору, Результат підбору параметра, що відображується в діалоговому вікні. Клацаємо на кнопці 0К, аби зберегти набутих значень клітин, що брали участь в операції. У клітку А1 отримуємо наближене значення х = 0,999872 (рис. 2). При цьому погрішність рішення (значення правої частини рівняння) — замість 0 у клітку В1 отримуємо - -0,00013.

рис. 2. Результати обчислень з прикладу 1

Таким чином, при значенні х = 0,999872 права частина рівняння lп х = 0 наближається до нуля (-0,00013). Зважаючи, що отриманий корінь це наближене рішення, його можна округлити до 1, тобто х = 1, що і є відомим аналітичним вирішенням цього рівняння.

Приклад

Найти рішення рівняння х² - Зх +2 = 0.

Рішення:

Рівняння має 2 корені. Рішення починаємо із знаходження першого кореня.

1. Відкрити новий робочий аркуш (команда Вставка > Аркуш).

Заносимо у клітину А1 орієнтовне значення першого кореня, наприклад, 3.

2. Заносимо у клітину В1 ліву частину рівняння, використовуючи як незалежну змінну заслання на клітину А1. Відповідна формула матиме вигляд = А1^2 - 3*А1 + 2.

2. Викликаємо процедуру Підбір параметра (команда Сервіс > Підбір параметра).

2. У полі Встановити у клітину вказуємо В1, в полі Значення задаємо 0 (права частина рівняння), в полі Змінюючи значення вічка вказуємо А1.

3. Клацаємо на кнопці ОК і отримуємо результат підбору, Результат підбору параметра, що відображується в діалоговому вікні. Клацаємо на кнопці 0К, аби зберегти набутих значень вічок, що брали участь в операції. Таким чином, у клітину А1 набуваємо наближеного значення x1 = 2,000048. При цьому точність рішення (значення правої частини рівняння) — замість 0 у клітину В1 отримуємо 4,85Е-05 (0,0000485).

4. Повторюємо розрахунок для другого кореня х2, задаючи у клітину А1 інше початкове значення, наприклад -3. Набуваємо значення другого кореня рівняння x2 = 0,9996.