3. Розв’язання системи лінійних рівнянь алгебри методом звичайних Жорданових виключень.

Розглянемо систему n лінійних рівнянь з n невідомими:

Причому rang (A)=n,

А - матриця системи;

С - розширена матриця, тобто матриця А з приєднаним справа стовпцем вільних членів.

Перепишемо систему у вигляді:

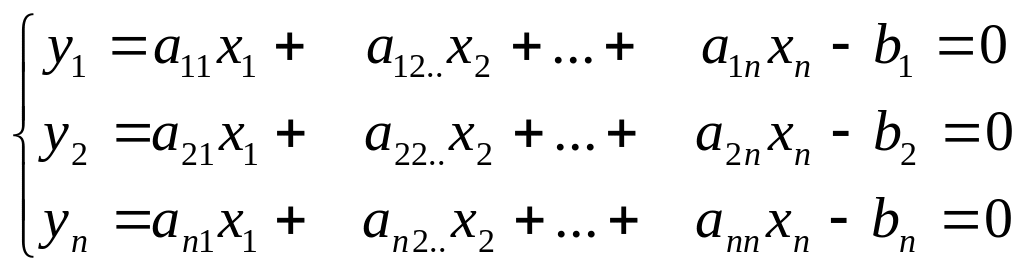
Запишемо систему в табличній формі:

	x1	x2 У2	...	xn	1
y1	a11	a12	...	a1n	-b1
y2	a21	a22	...	a2n	-b2
yn	an1	an2	...	an3	-bn

Після n послідовних кроків звичайних жорданових виключень отримаємо таблицю з вирішенням системи лінійних рівнянь алгебри:

	У1	У2	...	Уn	1
Х1	a11	a12	...	а 1n	1
Х2	a12	a22	...	a2n	2
Xn	an2	an2	...	an3	n

Оскільки у_i = 0 (i = 1,n), рішення запишемо у вигляді:

х₁ = ₁, х₂ = ₂ ., х_n = _n

Решта коефіцієнтів таблиці складає зворотну матрицю. Якщо при знаходженні вирішень системи рівнянь не ставиться завдання знаходження зворотної матриці, то після n кроків розв’язок системи знаходиться у останньому стовпчику (1) тому усі інші стовпчики можна викреслить. Таблиця розв’язку приймає вигляд:

Хj = 1
ХІ	1
Х2 . . .	2 . . .
Хn	n

4. Завдання оптимізації

Дуже широкий клас завдань складають завдання оптимізації або, як їх ще називають, екстремальні завдання. Звичайне їх рішення зв'язано з великою кількістю обчислень, що утрудняє їх рішення уручну. Нижче будуть розглянуті деякі типи завдань оптимізації: вирішення рівнянь з одним невідомим, завдання лінійного програмування і апроксимація функцій.