Дослідження систем лінійних рівнянь алгебри

При вирішенні системи лінійних рівнянь алгебри може статися, що визначник системи рівний нулю або число рівнянь не рівне числу невідомих. Тому вирішенню системи лінійних рівнянь алгебри повинно передувати дослідження, які виконуються в наступному порядку:

1. досліджувати чи є система рівнянь сумісною або несумісною, тобто чи має вона взагалі рішення;

2. якщо система сумісна то досліджувати чи є система рівнянь визначеною, тобто чи має вона єдине рішення або такі рішень багато;

3. якщо система сумісна і визначена знайти її єдине рішення;

4. якщо система сумісна і не визначена, то описати сукупність вирішень системи.

3. Звичайні Жорданові виключення

Розглянемо систему m лінійних функцій з n невідомими

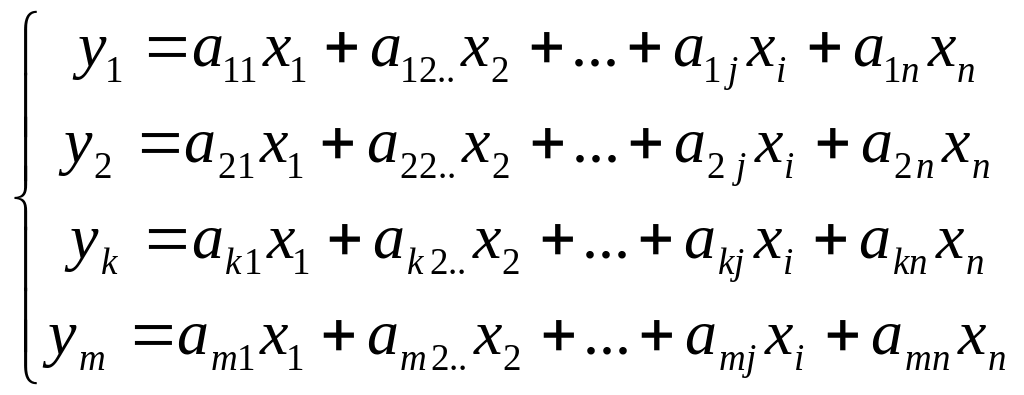                                         (3)

Х₁, Х₂, Х₃, ..., Х_n - незалежні змінні;

У₁, У₂, У₃, …, У _m - залежні змінні.

Цю систему можна записати скорочено: де i = 1, m

Представимо систему (3) у вигляді таблиці:

	x1	x2	.	xis	..	xn
y1	a11	a12	...	а1s	...	a1n
y2	a21	a22	...	a2s	...	а2 n
… уk …	… ak1 …	… аk2 …	... … …	… аks …	... … …	… аkn …
ym	am1	am2	...	ams	...	amn

Така таблиця називається жордановою. Перехід від цієї таблиці до системи (3) здійснюється таким чином: елементи a_Kj (k=1,m) к-го рядка множаться на відповідні незалежні змінні x_j (j=1,n), які розміщені у верхньому рядку, як назви стовпчіків. Отримані таким чином добутки складаються і прирівнюються до залежної у_k (k=1,m).

Систему (1) необхідно перетворити так, щоб залежна змінна у_k після перетворення стала незалежною, а незалежна змінна x_s - залежною. Така операція називається одним кроком Жорданових виключень. При цьому a_ks -називаєтся ключовим (головним) елементом; k-й рядок називається головним рядком, s-й стовчик - називається ключовим (головним) стовбцем.

Один крок звичайних Жорданових виключень з головним елементом a_ks зручно розбити на наступні операції:

1. головний елемент замінюється одиницею;

2. решта елементів головного стовпця залишається без змін:

3. решту елементів головного рядка змінюють знаки на протилежних;

4. елементи, які не належать головному рядку і головному стовпцю, визначаються за правилом прямокутника: b_ij=a_ij*a_ks-a_is*a_kj, де i, к-рядки; j, s - стовпці.

5. Усі елементи нової/отриманої таблиці ділимо на головний елемент.

Правило прямокутника:

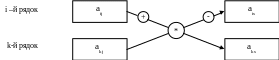
b_ij=a_ij*a_ks-a_is*a_kj, де i, к-рядки; j, s - стовпці.

І так, суть метода вираження незалежної змінної через залежну. Тобто отримання нової таблиці:

	x1	x2	.	уk xis	..	xn
y1	b11	b12	...	а1s	...	b1n
y2	b21	b22	...	a2s	...	b2 n
… xis …	… -ak1 …	… -аk2 …	... … …	… 1 …	... … …	… -аkn …
ym	bm1	bm2	...	ams	...	bmn

всі елементи якої потрібно поділити на головний (a_ks)