2. Системи лінійних рівнянь алгебри

1. Загальні відомості

Систему рівняння вигляду:

називають системою n-лінійних рівнянь з n-залежними.

Коефіцієнти рівнянь, записані у вигляді матриці А:

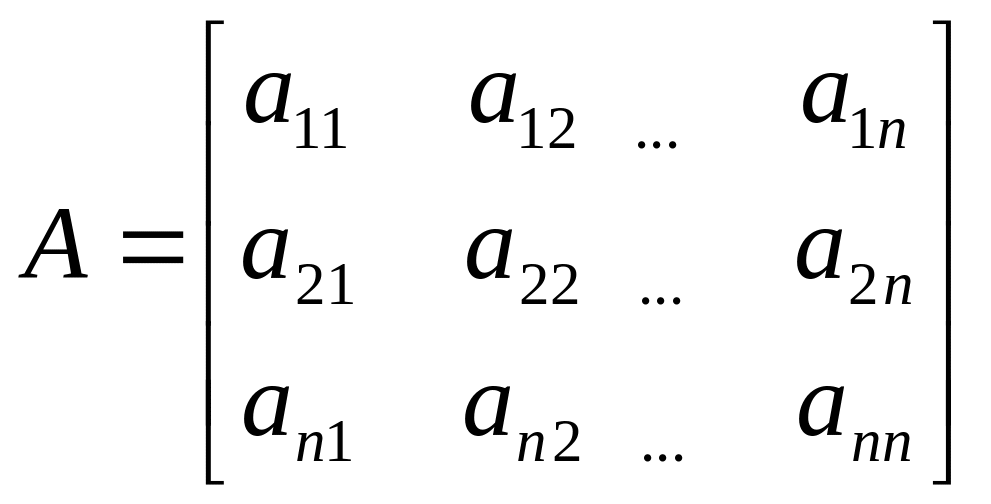
називають матрицею системи, а її визначника називають визначником системи.

Числа b_1, b_2, b_n називаються вільними числами.

Матриці системи, доповнені справа стовпцем вільних членів, називаються розширеною матрицею системи

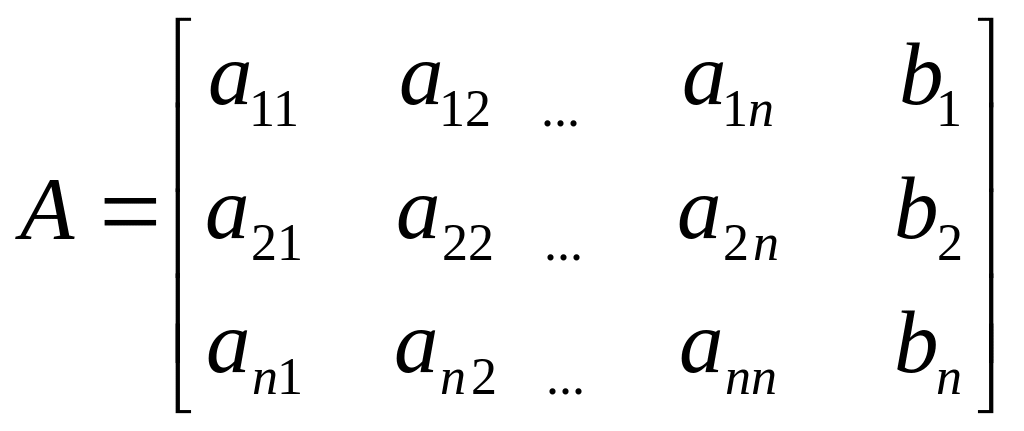
Якщо всі коефіцієнти стовпця вільних членів обертаються в нуль, то система лінійних рівнянь алгебри називається однорідною.

Сукупність чисел X1=λ1, X2= λ 2 , Xn= λ n, називається рішенням системи лінійних рівнянь алгебри, якщо кожне рівняння системи обертається в тотожність після підстановки в нього чисел λ i замість відповідних X_iі = 1,n.

Система лінійних рівнянь алгебри, що має хоч би одне рішення, називається сумісною, а якщо немає рішень - несумісною.

Сумісна система лінійних рівнянь алгебри називається визначеною, якщо вона має одне рішення і невизначеною, якщо має безліч рішень.

2. Метод Крамера

Хай дана система лінійних рівнянь алгебри mхn:

(1)

Якщо визначник матриці системи (1) не рівний нулю, то лінійне рівняння має рішення і при тому єдине. Обчислення системи лінійних рівнянь алгебри при цьому визначається по формулах Крамера:

X _j =∆j / ∆ j=1,n,

де ∆ - визначник матриці системи.

∆j – визначник, що отримується з визначника матриці системи, якщо в ньому замінити j-й стовпець стовпцем вільних членів.

Xi – рішення системи лінійних рівнянь алгебри.

Розв’язання системи лінійних рівнянь алгебри в Excel за методом Крамера

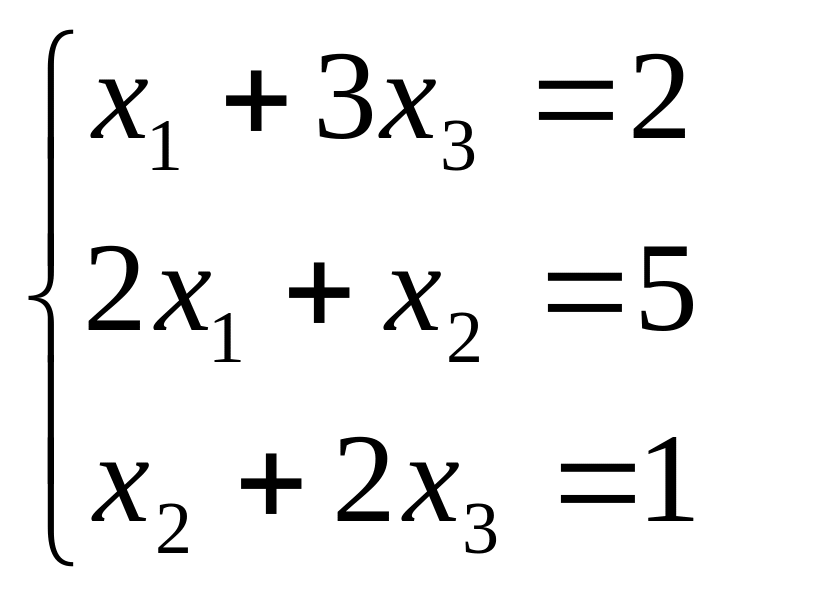
Якщо матриця А не вироджена, то

1. Введемо її в оболонку електронної таблиці: матриця А - блок (В2 : D4), вектор вільних членів В - блок (F2:F4).

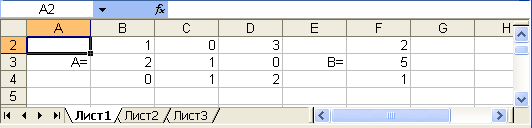
2. Нижче побудуємо три допоміжні матриці А1, А2, А3, які утворюються : А1 це копія матриці А в якій перший стовпчик заміняємо масивом В, А2 це копія матриці А в якій другий стовпчик заміняємо масивом В, А3 - копія матриці А, де третій стовпчик заміняємо масивом В.

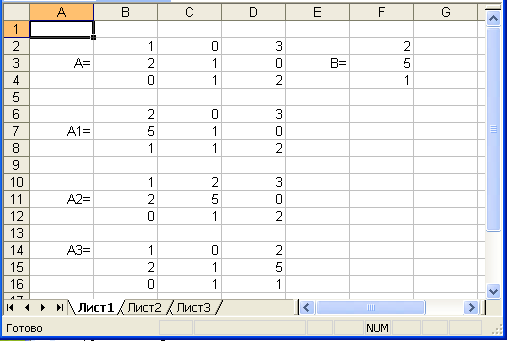
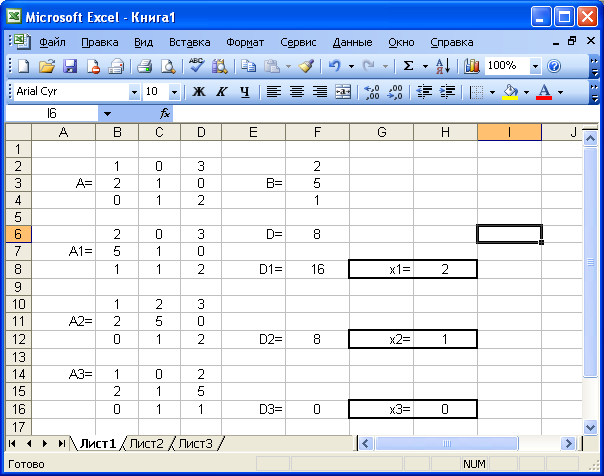
3. Знаходимо D визначник матриці А (fx → Математические → МОПРЕД → В2 : D4), D1 визначник матриці А1, D2 визначник матриці А2, D2 визначник матриці А2 .

4. Потім розраховуємо х1, х2, х3 за формулою хі= Dі / D

3. Матричний метод рішення системи лінійних рівнянь алгебри

Хай визначник системи відмінний від нуля. Позначимо матрицю-стовпець з невідомих через Х, а матрицю-стовпець з вільних членів через В:

Тоді, згідно правилу множення матриць, отримаємо:

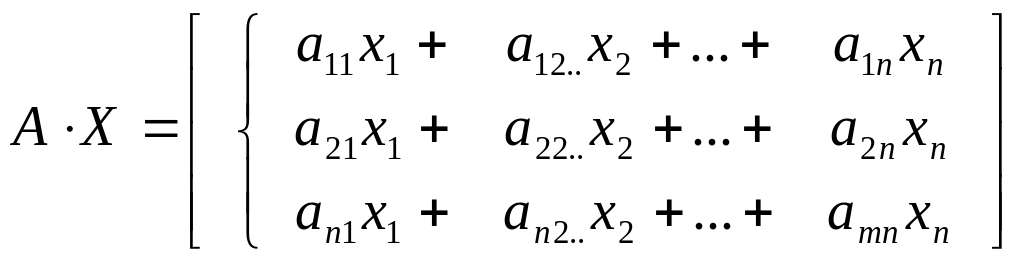
Використовуючи визначення рівності матриць, дану систему (1) можна записати таким чином:

А*Х=В - матричне рівняння (2)

Оскільки по умові |A|≠0, то для матриці А існує зворотна матриця А^-1:

А^-1*(А*Х)= А^-1*В

Але, оскільки А^-1*А=Е і Е*Х=Х, то отримуємо рішення матричного рівняння у вигляді:

Х= А^-1*В

Матрична форма розв’язання системи лінійних рівнянь в Excel

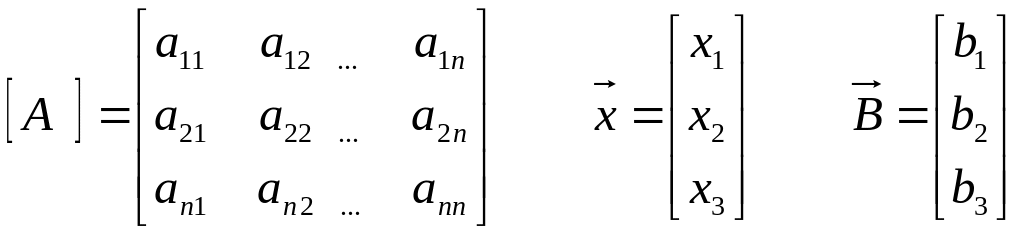
Якщо матриця А не вироджена, то

А^-1 А*Х = А^-1_* В => Х = А^-1_*В

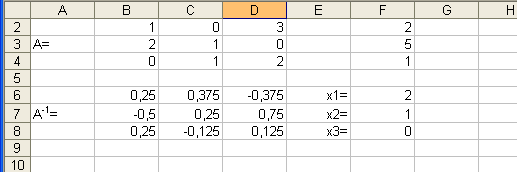
Знайдемо вирішення приведеної системи лінійних рівнянь алгебри:

1. Введемо її в оболонку електронної таблиці: матриця А - блок (В2 : D4), вектор вільних членів В - блок (F2:F4).

2. Знаходимо зворотну матрицю, використовуючи функцію МОБР() для клітини В6. Результат отримуємо в блоці В6 : D8 (fx → Математические → МОБР → В2 : D4) .

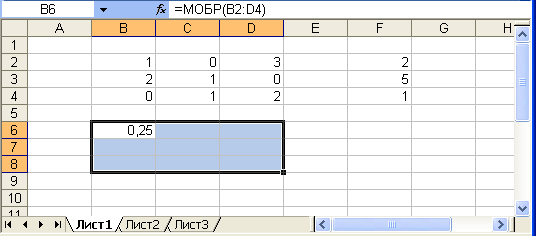
* Виділяємо В6 : D8 потім натиснути функціональну клавішу F2 і комбінацію клавіш Ctrl-Shift-Enter та отримаємо матрицю:

0,25	0,375	-0,375
-0,5	0,25	0,75
0,25	-0,125	0,125

3. Знаходимо вектор розв’язання системи рівнянь (блок F6 ... F8), помноживши [ А] ^-1 (блок В2 : D4) на В (блок F2:F4). Тобто fx → Математические → МУМНОЖ → Масив1 →В6 : D8 → Масив2→ F2:F4 та повторимо дії з попереднього пункту з зірочкою (*) для F6 : F8 та отримаємо рішення