Апроксимація декілька незалежних змінних

У тих випадках, коли змінна, що апроксимується у залежить від декількох незалежних змінних х_1,х₂,...,x_n,

підхід з побудовою лінії тренду не дає рішення. Тут можуть бути використані наступні спеціальні функції MS Excel:

ЛИНЕЙН и ТЕНДЕНЦИЯ для апроксимації лінійних функцій вигляду:

(15)

ЛГРФПРИБЛ и РОСТ для апроксимації показових функцій вигляду:

Функції ЛИНЕЙН и ЛГРФПРИБЛ (були розглянуті раніше) служать для обчислення невідомих коефіцієнтів а_0, a₁,..., а_n, у виразах (3.13) і (3.14) відповідно, а також коефіцієнтів детерміації (R²), значень критерію Фішера, стандартних помилок коефіцієнтів а_i, і ряду інших показників.

Функції ТЕНДЕНЦИЯ і РОСТ дозволяють знаходити крапки, лежачі на апроксимуючих кривих (3.13) і (3.14), відповідно, для значень коефіцієнтів а₀, а_1, ..., а_n, знайдених функціями ЛИНЕЙН и ЛГРФПРИБЛ.

Обидві функції мають однакові аргументи:

ТЕНДЕНЦИЯ(известные_значения_у;известные_значения_х;новые_значения_х;конст);

РОСТ(известные_значения_у;известные_зиачения_х;новые_зиачения_х;конст).

Тут:

О известные_значения_у — безліч значень у;

О известные_значения_х — безліч значень х;

О новые_значения_х — ті значення х, для яких необхідно визначити відповідні апроксимуючі або передбачені значення у. Новые_зна-чения_х повинні містити стовпець (або рядок) для кожної незалежної змінної, як і известные_зпачения_х. Якщо аргумент новые __значения_х опущений, то передбачається, що він збігається з аргументом известные_значения_х;

О конст — логічне значення, яке вказує, чи потрібне, аби константа а₀ була рівна 0 (для функції ТЕНДЕНЦИЯ) або 1 (для функції РОСТ). При цьому, якщо конст має значення ІСТИНА або опущено, то а₀ обчислюється звичайним способом, а якщо конст має значення ПОХИБКА, то а₀ вважається рівним 0 або 1 (рис. 19).

Приклад 6. Джерело радіоактивного випромінювання поміщене в рідину. Датчики розташовані на відстані (х₁) 20, 50 і 100 см від джерела. Виміри інтенсивності випромінювання (у, мРн) проводилися через 1,5 і 10 діб (х₂) після установки джерела. Результати вимірів (у) приведені в таблиці:

x1/x2	1	5	10
20	61,2	43,6	28,3
50	33,6	24,0	15,6
100	12,3	8,8	5,7

Необхідно апроксимувати дані рівнянням вигляду (15) і знайти невідомі параметри.

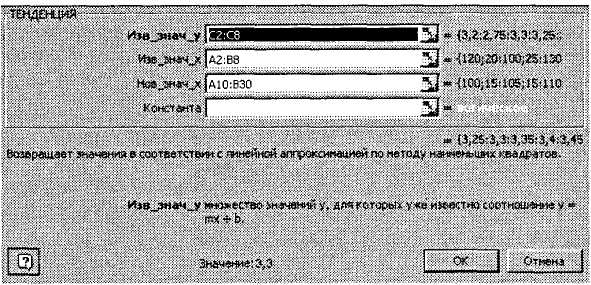
Рис. 19. Приклад заповнення діалогового вікна функції ТЕНДЕНЦИЯ

Рішення

1. Введемо дані в робочу таблицю: у клітину А1 - символ х_1, у клітину В1- х₂, у клітину С1 - у. У діапазон клітин А2:А10 внесемо значення х₁, у діапазон В2:В10 — значення x₂ і в діапазон С2:С10 — значення у (рис. 20).

	А	B	С
1	X1	X2	Y
2	20	1	61,2
3	50	1	33,6
4	100	1	12,3
5	20	5	43,6
6	50	5	24
7	100	5	8,8
8	20	10	28,3
9	50	10	15,6
10	100	10	5,7

Рис. 20. Вихідні дані з прикладу 3.7

2. Виділяємо блок клітин D1:F5 під масив результатів.

3. Оскільки рівняння для обчислення інтенсивності випромінювання має статечною характер (3.14), викликаємо функцію ЛГРФПРИБЛ (панель інструментів Стандартная, кнопка Вставка функции, робоче поле Категория тип Статистические, робоче поле Функция вигляд ЛГРФПРИБЛ).

4. Заповнюємо робочі поля: Изв_знач_у - С2:С10, Изв_знач_х - А2:В10, Стат - 1 (рис. 18). Натискуємо поєднання клавіш CTRL+SHIFT+ENTER.

5. В результаті в діапазоні D1:F5 отримаємо наступні дані:

0,918043	0,980162	99,70907
0,000337	3,7бЕ-05	0,003051
0,999983	0,003722	#Н/Д
174174,7	6	#н/д
4,8	8,31Е-05	#н/д

Тут перший рядок — значення коефіцієнтів а₂, а_1, а₀, відповідно, другий рядок — стандартні помилки цих коефіцієнтів, третій рядок — коефіцієнт детерміації R² і стандартна помилка у, четвертий рядок — значення критерію Фішера і число ступення свободи і нижній рядок — сума квадратів регресії і залишкова сума квадратів.

Таким чином, шукане апроксимуюче рівняння має вигляд:

y = 99,7*0,98^x1*0,92^x2.

Причому точність апроксимації дуже висока — R² = 0,99998.

Приклад 7. У басейні проводиться щоденна часткова зміна води. Є дані семиденних спостережень зміни рівня води в басейні (y) від тривалості заповнення водою (х₁) і часу випуску води (х₂).

XI	Х2	Y
120	20	3,2
100	25	2,8
130	20	3,3
100	15	3,3
110	23	3,0
105	26	2,8
112	16	3,3

Необхідно знайти значення рівня води в басейні залежно від тривалості заповнення x₁  [100; 130] і випуску води х₂  [15; 25] з кроком ∆ = 5 хвилин. Побудувати поверхню.

Рішення

1. Введемо дані в робочу таблицю: у клітину А1 — символ х_1, у клітину В1 — х₂, у клітину С1 — у. У діапазон клітин А2:А8 внесемо значення х_1, у діапазон В2:В8 — значення х₂ і в діапазон С2:С8 — значення у.

2. Введемо значення х₁, и х₂ для набуття розрахункових значень у відповідно до завдання: х₁  [100; 130] у діапазон А10:А30, а х₂  [15; 25] у діапазон В10:В30

(рис. 3.17).

3. Виділимо блок клітин С10:С30 під масив розрахункових (передбачених) значень у.

3. Оскільки рівняння для обчислення рівня води лінійне (3.13), викликаємо функцію ТЕНДЕНЦИЯ (панель інструментів Стандартная, кнопка Вставка функции, робоче поле Категория тип Статистические, робоче поле Функция вид ТЕНДЕНЦИЯ).

5. Заповнюємо робочі поля: Изв_знач_у — С2:С8, Изв_знач_х — А2:В8, Нов_знач_х — А10:В30 (рис. 3.15). Ctrl+Shift+Enter.

6. В результаті в діапазоні С10:С30 набудемо передбачених значень у (рис. 3.17).

7. Формуємо блок даних для побудови діаграми. Для цього введемо значення змінної х₁ у стовпець Е. Для цього в клітину Е1 вводимо символ х. У діапазон клітин Е2:Е8 — значення х₁  [100; 130] з кроком ∆ = 5 хвилин. У діапазон F1:H1 вводяться значення х₂ 15,20,30. Потім діапазон F2:H8 заповнюється відповідними розрахунковими значеннями у.

	А	В	С
9	Х1	Х2	Y
10	100	15	3,3
11	105	15	3,3
12	110	15	3,4
13	115	15	3,4
14	120	15	3,5
15	125	15	3,5
16	130	15	3,6
17	100	20	3,0
18	105	20	3,1
19	110	20	3,1
20	115	20	3,2
21	120	20	3,2
22	125	20	3,3
23	130	20	3,3
24	100	25	2,8
25	105	25	2,8
26	110	25	2,9
27	115	25	2,9
28	120	25	3,0
29	125	25	3,0
30	130	25	3,1

Рис. 21. Розрахункові значення у і відповідні ним значення х₁ і х₂ з прикладу 7

У результаті має бути отримана наступна таблиця (рис. 22).

E	F	G	H
X	15	20	25
100	3,3	3,0	2,7
105	3,3	3,0	2,8
110	3,4	3,1	2,8
115	3,4	3,1	2,9
120	3,5	3,2	2,9
125	3,5	3,2	3,0
130	3,6	3,3	3,0

Рис. 22. Дані з прикладу 7, підготовлені для побудови площини

8. Для побудови діаграми на панелі інструментів Стандартная необхідно натискувати кнопку Мастер диаграмм. У діалоговому вікні, що з'явилося Мастер диаграмм (крок 1 із 4): тип диаграммы вказуємо типа діаграми — Поверхность, і вигляд — Проволочная (прозора) поверхня (праву верхню діаграму в правому вікні). Після чого натискуємо кнопку Далее у діалоговому вікні.

9. У діалоговому вікні, що з'явилося Мастер диаграмм (крок 2 з 4): источник данных диаграммы необхідно вибрати вкладку Диапазон данных і в полі Диапазон мишею вказати інтервал даних F2:H8.

Далі необхідно вказати в рядках або стовпцях розташовані ряди даних. Це визначить орієнтацію осей X і Y. У прикладі перемикач Ряди в за допомогою покажчика миші встановимо в положення столбцах.

10. Вибираємо вкладку Ряд і в полі Подписи оси X вказуємо діапазон підписів. Для цього слід активізувати поле Підпису осі X, клацнувши в нім покажчиком миші, і ввести діапазон підписів осі X — Е2:Е8.

11. Вводимо значення підписів осі У. Для цього в робочому полі Ряд вказуємо перший запис Ряд 1 і в робоче поле Имя, активізувавши його покажчиком миші, вводимо перше значення змінної Y (х₂) — 15. Потім в полі Ряд вказуємо другий запис Ряд 2 і в робоче поле Имя вводимо друге значення змінної х₂ — 20. Аналогічно вказуємо х₂ = 25 замість запису Ряд 3. Після появи необхідних записів необхідно натискувати кнопку Далее.

12. У третьому вікні потрібно ввести заголовок діаграми і назви осей. Для цього необхідно вибрати вкладку Заголовки, клацнувши на ній покажчиком миші. Клацнувши в робочому полі покажчиком миші, ввести з клавіатури в поля Ось X (категорий), Ось Y (рядов данных) и Ось Z (значений) відповідні назви: х_1, х₂ і у.

13. Натискуємо кнопку Готово, і після невеликого редагування буде отримана діаграма зміни рівня води в басейні (рис. 23).

Рис. 23. Діаграма зміни рівня води в басейні залежно від співвідношення часу заповнення і випуску води (приклад 7)