II. Наступний крок для стандартних функцій, що залишилися.

Для цього необхідно побудувати діаграму для наших даних.

1. Оскільки тут необхідно будувати динаміку змін концентрації речовини відповідно до змін часу — будуватимемо діаграму Точечная.

Викликаємо Мастер диаграмм. У діалоговому вікні, що з'явилося, вибираємо типа діаграми Точечна, вид — левый верхний. Після натиснення кнопки Далее вказуємо діапазон даних — В1:В5 (за допомогою миші). Перевіряємо положення перемикача Ряды в: столбцах. Вибираємо вкладку Ряд і за допомогою миші вводимо діапазон підписів осі X: А2:А5. Натискує кнопку Далее, вводимо назву діаграми — Концентрація речовини, назва осей X і У: Час і Концентрація, відповідно. Натискуємо кнопку Готово.

Отриманий графік експериментальних даних.

3. Здійснимо апроксимацію отриманої кривої. Оскільки крива нагадує експоненту і з теоретичних міркувань найбільш вірогідний закон зміни — експоненціальний, доцільно апроксимувати криву зміни концентрації експоненціальною функцією. Для цього покажчик миші встановлюємо на одну з точок графіка і клацаємо правою кнопкою. У контекстному меню, що з'явилося, вибираємо пункт Добавить линию тренда. З'являється діалогове вікно Линия тренда.

У цьому вікні на вкладці Тип вибираємо типа лінії тренду — Експоненціальна. Потім відкриваємо вкладку Параметры і встановлюємо прапорці в поля показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации (R^2). Окрім цього, для того, щоб оцінити концентрацію речовини у водоймищі у момент викиду в полі Прогноз назад на встановлюємо 1 периодов. Після чого клацаємо на кнопці ОК. В результаті отримаємо на діаграмі апроксимуючу криву (рис. 15).

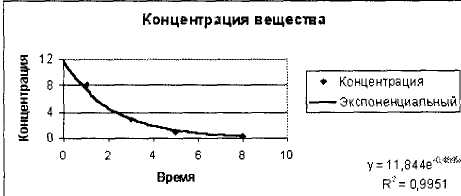
Рис. 15. Експериментальні дані, апроксимовані експоненціальною функцією з прикладу 4

Як видно з рис. 15, рівняння найкращої експоненціальної апроксимуючої функції для залежності концентрації від часу виглядає як

y = 11,844е^-0,4695x

При цьому точність апроксимації дуже висока — R² = 0,9951.

Побудуємо всі лінії тренду і порівняємо R²

Получимо:

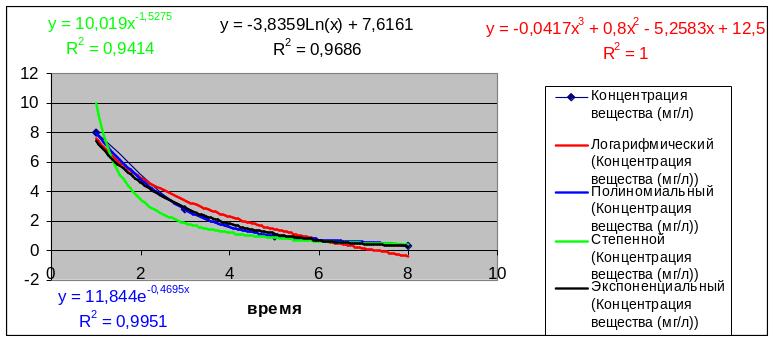
В результаті отриманих даних можна сказати, що R² краще в поліноміальної функції міри не нижче 3. Функція має вигляд y = -0,0417x3 + 0,8x2 - 5,2583x + 12,5.

Отже будуємо У(х) розрахункове для цієї функції в стовпчику N, в клітці N2 вводимо формулу = -0,0417*A2^3 + 0,8*A2^2 - 5,2583*A2 + 12,5 і вживаний для всіх значень х.

• Порахуємо відхилення У и У(х) розрахункове в стовпці О, тобто в клітці О2 вводимо формулу =B2-K2 і поширюємо для всіх У.

• Знаходимо для цього стовпця середнє в клітці О7, тобто вводимо формулу =СРЗНАЧ(N 2: N 5).

І так набуваємо наступних значень:

	К	L	M	N	O
1	У(х) лог.прибл	Відхилення У-У(х) логр.рибл		У(х) поліноміальна	Відхилення У-У(х) поліном
2	7,405822	0,59417848		8	0
3	2,895602	-0,09560173		2,7992	0,0008
4	1,132151	-0,13215115		0,996	0,004
5	0,276792	0,02320847		0,2832	0,0168
6		середнє відхилення			середнє відхилення
7		0,09740852			0,0054

Маємо R² для функцій поліноміальна і логарифмічного наближення і середні відхилення їх значень, можемо зробити вивід, що кращою є апроксимуюча функція для наших вихідних даних – поліноміальна.

Отже можемо зробити прогноз, за даними нашої умови, тобто знайти у(0) і у(2). Підставимо значення х - 0 і 2 у стовпчик А (клітки А6 і А7) і отримаємо в стовпці N (клітках N6 и N7) прогнозні значення рівня концентрації на момент часу викиду (0) і 2 часа: 12,5 і 4,8498

!!! Інколи вихідні дані при вирішенні завдань такого типа потрібно реорганізовувати, наприклад у вихідних даних значення Х типа дата, час .. В цьому випадку необхідно дані упорядкувати спочатку (сортування) потім замінити порядковими номерами, а потім застосовувати розглянутий раніше алгоритм. Або апроксимувати за допомогою побудови лінії тренду, але тип діаграми Графік.

Приклад 5. Досліджувати характер зміни з часом рівня виробництва деякої продукції і підібрати апроксимуючу функцію, маючи в своєму розпорядженні наступні дані:

Рік	Виробництво продукції
1997	17,1
1998	18,0
1999	18,9
2000	19,7
2001	19,7

Рішення

Спочатку перевіримо дві вбудовані функції лінійну і логарифмічного наближення.

Перший

1. Для побудови діаграми, перш за все, необхідно ввести дані в робочу таблицю. Вводимо в клітину А1 слово Рік. Потім в клітини А2:А6 послідовно вводимо роки, починаючи з 1997. Далі в клітину В1 заносимо слово Продукція і встановлюємо табличний курсор у клітину В2. Тут повинне бути значення 17,1 відповідне значенню року у клітині А2. Аналогічно заповнюємо клітини ВЗ:В6.

2. Далі по введених в робочу таблицю даним необхідно побудувати діаграму. Оскільки тут необхідно будувати динаміку змін виробництва продукції, не прив'язуючись до конкретного року, а від вільних змінних — виберемо діаграму График.

На панелі інструментів викликаємо Мастер диаграмм. У діалоговому вікні, що з'явилося, вибираємо типа діаграми График, вигляд — лівий середній. Після натиснення кнопки Далее вказуємо діапазон даних — В1:В6 (за допомогою миші). Перевіряємо положення перемикача Ряды у: стовпцях. Вибираємо вкладку Ряд і за допомогою миші вводимо діапазон підписів осі X: А2:А6. Натискує кнопку Далее, вводимо назву діаграми — Виробництво продукції, назва осей X і У: Роки і Умовні одиниці, відповідно. Натискуємо кнопку Готово.

Отриманий графік експериментальних даних.

3. Здійснимо апроксимацію отриманої кривої поліноміальною функцією другого порядку, оскільки крива досить гладка і не сильно відрізняється від прямої лінії. Для цього покажчик миші встановлюємо на одну з точок графіка і клацаємо правою кнопкою. У контекстному меню, що з'явилося, вибираємо пункт Добавить линию тренда. З'являється діалогове вікно Линия тренда (рис. 16).

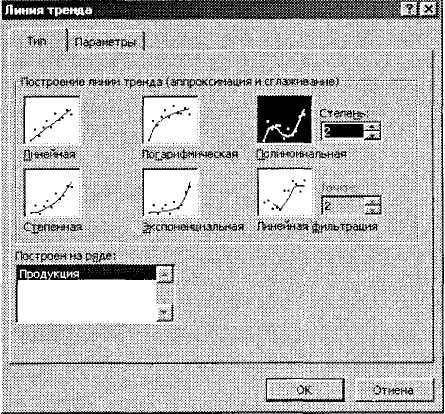
Рис. 16. Вкладка Тип діалогового вікна Лінія тренду

У цьому вікні на вкладці Тип вибираємо тип лінії тренду — Поліноміальна і встановлюємо ступень — 2. Потім відкриваємо вкладку Параметры (рис. 17) і встановлюємо прапорці в поля показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации (R^2). Після чого потрібно клацнути на кнопці ОК. В результаті отримаємо на діаграмі апроксимуючу криву (рис. 18).

Як видно з рис. 3.11, рівняння найкращої поліноміальної апроксимуючої функції для деяких відвернутих значень х (1, 2, 3,...) виглядає як

y = -0,14x² +1,5х+ 15,66. При цьому точність апроксимації досить висока — R² = 0,986.

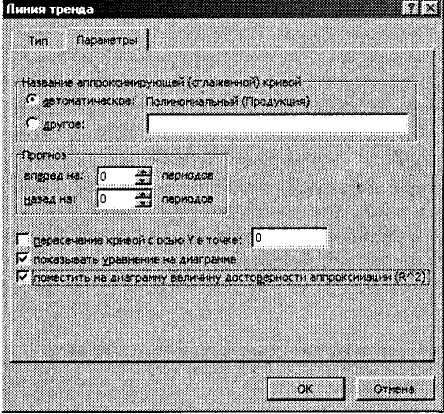
Рис. 17. Вкладка Параметри діалогового вікна Лінія тренду

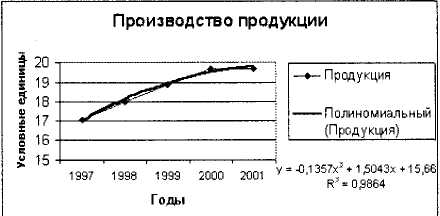
Рис. 18. Експериментальні дані, апроксимовані поліноміальною кривою, з прикладу 5

4. Спробуємо поліпшити якість апроксимації вибором іншого типа функції (можливо адекватнішого). Тут можливим варіантом представляється логарифмічна функція. Для цього повторюємо операції п. 3. за винятком того, що у вікні Линия тренда на вкладці Типа вибираємо тип лінії тренду — Логарифмічна.

В результаті отримаємо інший варіант апроксимації — логарифмічною кривою (рис. 19).

Як можна бачити з рис. 3.12, рівняння найкращої логарифмічної апроксимуючої функції декілька поступається по точності апроксимаціями поліноміальної кривої — R² = 0,9716 < 0,986. Тому якщо немає яких-небудь теоретичних міркувань, то можна вважати, що найкращою апроксимацією є апроксимація поліноміальною функцією другого ступення (з двох розглянутих варіантів).

Другий:

При виконанні не забудьте стовпець х розглядати як номер по порядку для року.!!!!

Далі для розв’язку задачі потрібно опрацювати алгоритм що наданий у прикладі 4.