I. Спочатку перевіримо дві вбудовані функції лінійну і логарифмічного наближення.
Для побудови діаграми, перш за все, необхідно ввести дані в робочу таблицю. Вводимо в клітину А1 слово Час. Потім в клітини А2:А5 послідовно вводимо час: 1,3,5, 8. Далі в клітину В1 заносимо слово Концентрація і в діапазон В2:В5 вводимо відповідні концентрації речовини, де час розглядатимемо як Х, концентрацію – У.
Для цього скористаємося вбудованою статистичною функцією ЛИНЕЙН.
Оскільки лінійна функція у=а0+а1х, потрібно знайти коефіцієнти а0 и а1 и R2 (коефіцієнт детерміації).
Виділяємо область 5 х 2 (2 (стовпці) – кількість коефіцієнтів аi, 5 (рядки) – знайдені дані (стандарт)): D3:E7.
Викликаємо вбудовану статистичну функцію ЛИНЕЙН
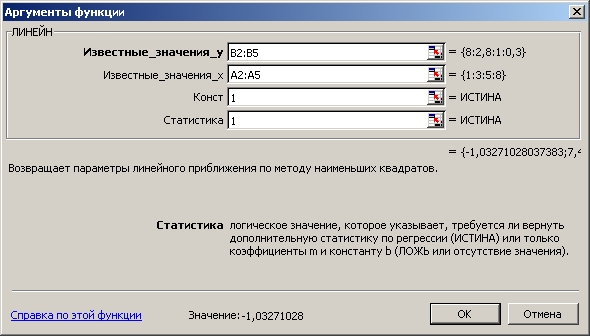
Заповнюємо виділену область D3:E7 – <F2>, <Ctrl>+<Shif>+<Enter>
Отримаємо наступні дані:
|
А |
В |
С |
D |
E |
F |
1 |
Час (година) |
Концентрація речовини (мг/л) |
|
Лінійна функція у=а0+а1х |
|
|
2 |
1 |
8 |
|
а1 |
а0 |
|
3 |
3 |
2,8 |
аi |
-1,03271 |
7,414019 |
|
4 |
5 |
1 |
відхилення а0 |
0,381803 |
1,899445 |
|
5 |
8 |
0,3 |
R^2 |
0,785318 |
1,9747 |
|
6 |
|
|
к. Фішерра |
7,316083 |
2 |
степень свободы |
7 |
|
|
кв.відхилення |
28,52862 |
7,798879 |
|
Теперь скористаємося вбудованою статистичною функцією ЛГРФПРИБЛ.
Оскільки функція логарифмічного наближення має вигляд у=а0*а1х, потрібно знайти коефіцієнти а0 и а1 и R2 (коефіцієнт детерміації).
Виділяємо також область 5 х 2 (2 (стовпці) – кількість коефіцієнтів аi, 5 (рядки) – знайдені дані (стандарт)): Н3:I7.
Викликаємо вбудовану статистичну функцію ЛГРФПРИБЛ.
Повторимо всі дії як для функції ЛИНЕЙН і отримаємо:
|
А |
В |
G |
Н |
I |
J |
1 |
Час (година) |
Концентрація речовини (мг/л) |
|
Функція логарифмічного наближення у=а0а1х |
|
|
2 |
1 |
8 |
|
а1 |
а0 |
|
3 |
3 |
2,8 |
аi |
0,625292 |
11,84378 |
|
4 |
5 |
1 |
відхилення а0 |
0,023271 |
0,115771 |
|
5 |
8 |
0,3 |
R^2 |
0,995111 |
0,120358 |
|
6 |
|
|
к. Фішерра |
407,113 |
2 |
міра свободи |
7 |
|
|
кв.відхилення |
5,897432 |
0,028972 |
|
4. Порівнюємо значення R2 для обох функцій, для функції логарифмічного наближення R2 = 0,995111, воно є кращим ( великим і прагне до 1).
Будуємо стовпець (К) значень для цієї функції, тобто. в клітині К2 вводим формулу =$I$3*$H$3^A2, де $I$3 значення коефіцієнта а0, $H$3 – а1, A2 – х, і вживаний для всіх значень х.
Порахуємо відхилення У и У(х) розрахункове в стовпці L, т.е. у клітині L2 вводимо формулу =B2-K2 і поширюємо для всіх У.
Знаходимо для цього стовпця середнє в клітці L7, тобто. вводимо формулу =СРЗНАЧ(L2:L5).
І так набуваємо наступних значень:
|
А |
В |
с |
К |
L |
1 |
Час (година) |
Концентрація речовини (мг/л) |
|
У(х) лог.прибл |
Відхилення У-У(х) логр.рибл |
2 |
1 |
8 |
|
7,405822 |
0,59417848 |
3 |
3 |
2,8 |
|
2,895602 |
-0,09560173 |
4 |
5 |
1 |
|
1,132151 |
-0,13215115 |
5 |
8 |
0,3 |
|
0,276792 |
0,02320847 |
6 |
|
|
|
|
середнє відхилення |
7 |
|
|
|
|
0,09740852 |