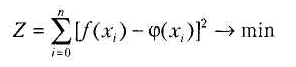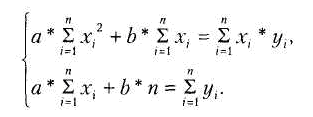5. Апроксимація експериментальних даних

На практиці часто доводиться стикатися із завданням про згладжування експериментальних залежностей або завданням апроксимації. Апроксимацією називається процес підбору емпіричної формули (х) для встановленої з досвіду функціональної залежності y=f(x). Емпіричні формули служать для аналітичного представлення дослідних даних.

Одна незалежна змінна

Зазвичай завдання апроксимації розпадається на дві частини. Спочатку встановлюють вигляд залежності y=f(x) і, відповідно, вигляд емпіричної формули, тобто вирішують, чи є вона лінійною, квадратичною, логарифмічною або який-небудь інший. Після цього визначаються чисельні значення невідомих параметрів вибраної емпіричної формули, для яких наближення до заданої функції виявляється найкращим. Якщо немає яких-небудь теоретичних міркувань для підбору вигляду формули, зазвичай вибирають функціональну залежність з числа найбільш простих, порівнюючи їх графіки з графіком заданої функції. Після вибору вигляду формули визначають її параметри. Для найкращого вибору параметрів задають міру близькості апроксимації експериментальних даних. У багатьох випадках, особливо якщо функція f(х) задана графіком або таблицею (на дискретній безлічі крапок), для оцінки міри наближення розглядають різниці f (х_і)-  (х_і) для точек х₀, х₁,…,х_п . Існують різні заходи близькості і, відповідно, способи рішення цієї задачі. Деякі з них дуже прості, швидко наводять до результату, але результат цей є сильно наближеним. Інші точніші, але і складніші. Звичайне визначення параметрів при відомому вигляді залежності здійснюють по методу найменших квадратів. При цьому функція (х) вважається найкращим наближенням до f(х), якщо для неї сума квадратів нев'язок _і або відхилень «теоретичних» значень (х_і), знайдених по емпіричній формулі, від відповідних дослідних значень у_і ,

( 13)

має найменше значення в порівнянні з іншими функціями, з числа яких вибирається шукане наближення.

Використовуючи методи диференціального числення, метод найменших квадратів формулює аналітичні умови досягнення сумою квадратів відхилень (13) свого найменшого значення. Так, якщо функція (х) сповна визначається своїми параметрами k, l, m, ..., то найкращі (у вказаному сенсі (13)) значення цих параметрів знаходяться з вирішення системи рівнянь. Наприклад. у простому випадку, коли функція (х) представлена лінійним рівнянням у = а х+ b, система має вигляд:

( 14 )

У простому випадку завдання апроксимації експериментальних даних виглядає таким чином.

Хай є якісь дані, отримані практичним дорогою (в ході експерименту або спостереження), які можна представити парами чисел (х; в). Залежність між ними відображає таблиця:

X	X1	………..Хn
У	У1	………..Уn

На основі цих даних потрібно підібрати функцію у = (х), яка щонайкраще згладжувала б експериментальну залежність між змінними і по можливості точно відображала загальну тенденцію залежності між х і y, виключаючи погрішності вимірів і випадкові відхилення. Це означає, що відхилення y_i - y_i(x_i) у якомусь сенсі були б найменшими. Наприклад, в сенсі (13).

З'ясувати вигляд функції можна або з теоретичних міркувань, або аналізуючи розташування крапок (х_n; у_n) на координатній площині.

Наприклад, хай крапки розташовані так, як показано на рис. 7.

Враховуючи те, що практичні дані отримані з деякою погрішністю, обумовленою неточністю вимірів, необхідністю округлення результатів і т. п., природно передбачити, що тут має місце лінійна залежність у = а х+ b.

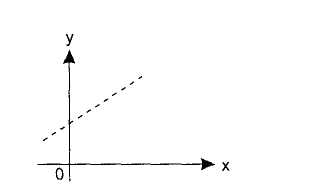
Рис. 7. Можливий варіант розташування експериментальних крапок

Аби функція набрала конкретного вигляду, необхідно якимсь чином обчислити а і b. Для цього можна вирішити систему (14).

Розташування експериментальних крапок у вигляді кривої на рис. 8 наводить на думку, що залежність назад пропорційна і функцію (x) потрібно підбирати у вигляді у = а + b/х. Тут також необхідно обчислити параметри а і b.

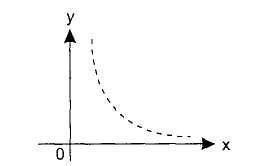
Рис. 8. Інший варіант розташування експериментальних крапок

Таким чином, розташування експериментальних крапок може мати самий різний вигляд, і кожному відповідає конкретний тип функції.

Побудова емпіричної функції зводиться до обчислення вхідних в неї параметрів, так аби зі всіх функцій такого вигляду вибрати ту, яка краще за інших описує залежність між величинами, що вивчаються. Тобто сума квадратів різниці між табличними значеннями функції в деяких крапках і значеннями, обчисленими за отриманою формулою, має бути мінімальна.

У MS Excel апроксимація експериментальних даних здійснюється шляхом побудови їх графіка (x - відвернуті величини) або точкового графіка (х — має конкретні значення) з подальшим підбором відповідної апроксимуючої функції (лінії тренду). Можливі наступні варіанти функцій:

1. Лінійна — у = ах + b. Зазвичай застосовується в простих випадках, коли експериментальні дані зростають або убувають з постійною швидкістю.

2. Поліноміальна — у = а₀ + а₁х + а₂х² + ... + а_пхⁿ, де до шостого порядку включно (п ≤ 6), a_і - константи. Використовується для опису експериментальних даних, що поперемінно зростають і убувають. Міра полінома визначається кількістю екстремумів (максимумів або мінімумів) кривої. Поліном другої міри може описати лише один максимум або мінімум, поліном третьої міри може мати один або два екстремуми, четвертій мірі — не більше трьох екстремумів і так далі

3. Логарифмічна — у = аlnх + b, де a і b — константи, ln -функція натурального логарифма. Функція застосовується для опису експериментальних даних, які спочатку швидко зростають або убувають, а потім поступово стабілізуються.

4. Степенева — у = bх^a, де а і b — константи. Апроксимація статечною функцією використовується для експериментальних даних з швидкістю росту, що постійно збільшується (або що убуває). Дані не повинні мати нульових або негативних значень.

5. Експоненціальна — у = bе^ax, де а і b — константи, е — підстава натурального логарифма. Застосовується для опису експериментальних даних, які швидко зростають або убувають, а потім поступово стабілізуються. Часто її використання витікає з теоретичних міркувань.

6. Є ще одна вбудована функція – Логарифмічного наближення - у = bа^х, де a и b— константи. Функція застосовується для опису експериментальних даних, які спочатку швидко убувають або зростають, а потім поступово стабілізуються.

Міра близькості апроксимації експериментальних даних вибраною функцією оцінюється коефіцієнтом детерміації (R²). Таким чином, якщо є декілька відповідних варіантів типів апроксимуючих функцій, можна вибрати функцію з великим коефіцієнтом детерміації (прагнучим до 1).

Для здійснення апроксимації на діаграмі експериментальних даних необхідно клацанням правої кнопки миші викликати випливаюче контекстне меню і вибрати пункт Добавить линию тренда. У діалоговому вікні, що з'явилося Линия тренда на вкладці Тип вибирається вигляд апроксимуючої функції, а на вкладці Параметры задаються додаткові параметри, що впливають на відображення апроксимуючої кривої.

Обі функції мають однакові параметри:

ЛИНЕЙН(известные_значения_у;известные_значения_х;конст;статистика) ЛГРФПРИБЛ(известные_значения_у;известные_значения_х;конст;статистика) Здесь:

О известные_значения_у — безліч спостережуваних значень у з виразів (15), (16);

О известные _значения_х — безліч спостережуваних значень х_1, х₂, ...,х_n. Причому, якщо масив известные_значения_у має один стовпець, то кожен стовпець масиву известные_значения_х інтерпретується як окрема змінна, а якщо масив известные_значения_у має один рядок, то тоді кожен рядок масиву известные_значения_х інтерпретується як окрема змінна;

О конст — логічне значення, яке вказує, чи потрібне, аби константа а₀ була рівна 0 (для функції ЛИНЕЙН) або 1 (для функції ЛГРФПРИБЛ).

При цьому, якщо конст має значення ІСТИНА або опущено, то a₀ обчислюється звичайним способом, а якщо конст має значення ПОХИБКА, то а₀ вважається рівним 0 або 1;

О статистика — логічне значення, яке вказує, чи потрібно обчислювати додаткову статистику по регресії, якщо введено значення ІСТИНА, то додаткові параметри обчислюються, якщо ПОХИБКА, то — немає (рис. 14).

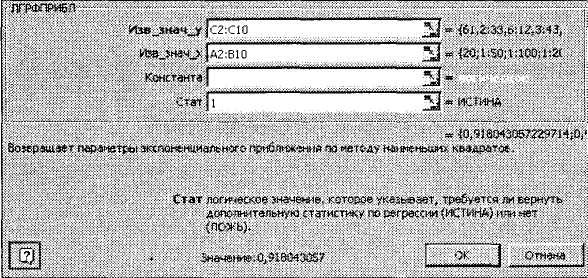
Рис. 14. Приклад заповнення діалогового вікна функції ЛГРФПРИБЛ

Для здійснення апроксимації на діаграмі експериментальних даних необхідно клацанням правої кнопки миші викликати випливаюче контекстне меню і вибрати пункт Добавить линию тренда. У діалоговому вікні, що з'явилося Линия тренда на вкладці Тип вибирається вигляд апроксимуючої функції, а на вкладці Параметры задаються додаткові параметри, що впливають на відображення що апроксимує криву.

Приклад 4, Після викиду отруйної речовини його концентрація (мг/л) у водоймищі змінювалася відповідно до наступної таблиці:

Час після викиду (година)		Концентрація речовини (мг/л)
1	8,0
3	2,8
5	1,0
8	0,3

Визначити вигляд функціональної залежності зміни концентрації речовини від часу і оцінити його концентрацію у водоймищі у момент викиду та через дві години.

Рішення