Лінійне програмування

У разі, коли цільова функція (4), що оптимізується, і обмеження (5) лінійні, завдання оптимізації вирішується методами лінійного програмування і зазвичай називається завданням лінійного програмування. Завдання лінійного програмування полягає в знаходженні r змінних x₁, x₂ ...,x_n що мінімізують дану лінійну функцію (цільову функцію):

Z=f(x₁, x₂,...,x_r) = c₁x₁ + с₂x₂ + … + c_rx_r , (7)

(або що максимізувала — Z) при лінійній обмеженнях-рівності:

А_i1х₁ + a_i2x₂ + ...+ a_itx_r = А_i где i = 1, 2,..., п (8)

і лінійних ограничениях-неравенствах:

А_i1х₁ + a_i2x₂ + ...+ a_itx_r  В_i где i = 1, 2,..., т. (9)

Часто завдання лінійного програмування (7-9) зводять шляхом введення у разі потреби допоміжних змінних до стандартної форми (основному завданню лінійного програмування). При цьому потрібно мінімізувати цілеву функцію:

Z=f(x_i,x₂,...х_n) = c₁x₁ + c₂x₂ + ... + с_nx_n (10)

при m < п лінійній обмеженнях-рівності

a_i1x₁ + a_i2x₂ + ... + а_inх_n = b_i, де i = 1, 2, ….т (11)

і п лінійних обмеженнях-нерівностей

х_k  0, де k =1,2,…, n. (12)

Допустимим рішенням (планом) задачі лінійного програмування є впорядкована безліч чисел (х1, х2 ..., хn), що задовольняють обмеженням (11) і (12). Це крапка в n-мірному просторі. Допустиме рішення, що мінімізує цільову функцію (10), називається оптимальним рішенням (оптимальним планом).

Найчастіше оптимальне рішення, якщо воно існує, є і єдиним. Проте можливі випадки, коли оптимальних рішень незліченна безліч.

Процес рішення задачі лінійного програмування зазвичай складається з ряду етапів:

• 1-й етап: осмислення завдання, виділення найбільш важливих якостей, властивостей, ве­личин, параметрів. Це можна робити, складаючи схеми, таблиці, графіки і т. п.;

• 2-й етап: введення позначень (невідомих). Бажано обмежуватися як можна меншою кількістю невідомих, виражаючи по можливості одні величини через інших;

• 3-й етап: створення цільової функції. Зазвичай як мета можуть виступати максимальна вартість всього об'єму продукції, максимальний прибуток, мінімальні витрати і тому подібне Цільова функція записується у вигляді (7) або (10).

• 4-й етап: складання системи обмежень, яким повинні задовольняти введені величини (8), (9) або (10) (11).

• 5-й етап: рішення задачі на комп'ютері.

Інструментом для пошуку вирішень завдань оптимізації в Excel служить процедура Пошук рішення (Сервіс > Пошук рішення). При цьому відкривається діалогове вікно Пошук рішення. Воно містить наступні робочі поля:

Встановити цільове клітину — служить для вказівки цільового вічка, значення якої необхідно максимізувати, мінімізувати або встановити рівним заданому числу. Це клітину повинне містити формулу:

• Рівною — служить для вибору варіанту оптимізації значення цільового вічка (максимізація, мінімізація або підбір заданого числа). Аби встановити число, необхідно ввести його в поле;

• Змінюючи вічка — служить для вказівки вічок, значення яких змінюються в процесі пошуку рішення до тих пір, поки не будуть виконані накладені обмеження і умова оптимізації значення вічка, вказаного в полі Уста­новіть цільове клітину;

• Передбачити — використовується для автоматичного пошуку вічок, що впливають на формулу, заслання на яку дана в полі Встановити цільове клітину. Результат пошуку відображується в полі Змінюючи вічка;

• Обмеження — служить для відображення списку граничних умов поставленого завдання;

• Додати — використовується для відображення діалогового вікна Додати обмеження;

• Змінити — застосовується для відображення діалогового вікна Змінити обмеження;

• Видалити — служить для зняття вказаного обмеження;

• Виконати — використовується для запуску пошуку рішення поставленої задачі;

• Закрити — служить для виходу з вікна діалогу без запуску пошуку рішення поставленної задачі. При цьому зберігаються установки, зроблені у вікнах діалогу, що з'являлися після натиснень на кнопки Параметри, Додати, Змінити або Видалити;

• Параметри — застосовується для відображення діалогового вікна Параметри пошуку рішення, в якому можна завантажити або зберегти модель, що оптимізується, і вказати передбачені варіанти пошуку рішення;

• Відновити — служить для очищення полий вікна діалогу і відновлення значень параметрів пошуку рішення, використовуваних за умовчанням.

Розглянемо приклади вирішення завдань оптимізації.

Розглянемо приклади вирішення завдань оптимізації двох класів ЗЛП і транспортні.

Приклад 3 – приклад клас ЗЛП. У ресторані готуються фірмові блюда трьох видів (блюдо А, блюдо В і блюдо З) з використанням при приготуванні інгредієнтів трьох видів (інградієнт 1, інгредієнт 2 і інгредієнт 3). Витрата інгредієнтів в грамах на блюдо задається наступною таблицею:

Вид ингредиента	Блюдо А	Блюдо В	Блюдо С
Інгредієнт 1 Інгредієнт 2 Інгредієнт 3	20 20 20	50 0 10	10 40 10

Вартість приготування блюд однакова (100 руб).

Щодня в ресторан поступає 5 кг інгредієнта 1 і по 4 кг інгредієнтів видів 2 і 3. Яке оптимальне співвідношення денного виробництва блюд різного вигляду, якщо виробничі потужності ресторану дозволяють використовувати весь запас продуктів, що поступили?

Рішення:

• Для вирішення завдання введемо позначення: хай х₁ — денний випуск блюда А; х₂ — денний випуск блюда В; х₃ — денний випуск блюда С.

• Складемо цільову функцію — вона полягає в знаходженні (максимальною) вартості випущених ресто­раном блюд:

Z=100*x₁ + 100*х₂+ 100*х₃.

• Визначимо наявні обмеження (керуючись умовою / таблицею):

1. 20*х₁ + 50*х₂+10*х₃  5000; (витрата ІНГРАДІЄНТА 1 не більш 5 кг)

2. 20 * х₁ + 0 * х₂ + 40 * х₃  4000; (витрата ІНГРАДІЄНТА 2 не більш 4 кг)

3. 20* х₁ + 10*х₂ + 10*х₃ 4000. (витрата ІНГРАДІЄНТА 3 не більш 4 кг)

Крім того, оскільки не можна реалізувати частину блюда і кількість блюд не може бути негативним, додамо ще ряд обмежень:

1. х₁  0;

2. x₂  0;

3. x₃  0;

4. х₁ — ціле;

5. х₂ — ціле;

6. х₃ — ціле.

Тепер можна приступити до рішення задачі на комп'ютері.

1. Відкриємо новий робочий аркуш.

2. У клітини В3, В4 і В5 занесемо денний запас продуктів — числа 5000, 4000 і 4000 відповідно.

3. У клітини D2, Е2, F2 занесемо початкові значення невідомих x₁, x₂ і х₃ (нулі) — надалі значення цих вічок будуть підібрані автоматично і виділимо заливкою.

4. У клітинах діапазону D3: F5 розмістимо таблицю витрати інгредієнтів.

5. У клітинах С3:С5 вкажемо формули для розрахунку витрати інгредієнтів по видах. У клітині В2 формула матиме вигляд =$С$1*С2 + $D$1*D2 + $E$1*E2, а останні формули можна отримати методом автозаповнення (копіювання-поширення).

6. У клітину G2 занесемо формулу цільової функції =100*( D2+ Е2+ F2). Результат введення даних в робочу таблицю представлений на рис. 3.

	А	B	с	D	Е	F	G
1		Запас		Блюдо А	Блюдо В	Блюдо С
2				0	0	0	0
3	Ингредиент 1	5000	0	20	50	10
4	Ингредиент 2	4000	0	20	0	40
5	Ингредиент 3	4000	0	20	10	10

Рис. 3. Результат введення даних з прикладу 3

7. Дамо команду Сервіс > Пошук рішення — відкриється діалогове вікно Пошук рішення.

8. У полі Установить целевую клітину мишею вкажемо клітину, що містить значення, що оптимізується (G2) (рис. 4). Встановимо перемикач Равною в положення максимальному значенню (потрібний максимальний обсяг виробництва).

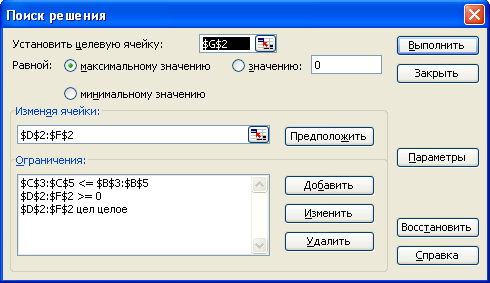
Рис. 4. Приклад заповнення діалогового вікна Поиск решения

9. У полі Змінюючи клітину мишею задамо діапазон підбираємих параметрів (невідомих х_i) — D2: F2.

10. Аби визначити набір обмежень, клацнемо на кнопці Добавить. У діалоговому вікні Додавання обмеження в полі Ссылка на клітину мишею вкажемо діапазон C3:C5. В якості умови задамо <=. У полі Ограничение мишею задамо діапазон B3:B5 (рис. 5). Ця умова вказує, що добова витрата інгредієнтів не повинна перевершувати запасів. Клацнемо на кнопці ОК.

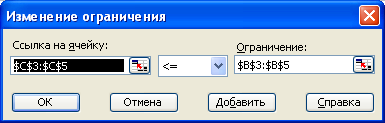
Рис. 5. Приклад заповнення діалогового вікна Додавання обмеження

11. Знову клацнемо на кнопці Добавить. У полі Ссылка на клітину вкажемо діапазон D2: F2. Як умова задамо >=. У полі Обмеження задамо число 0. Ця умова вказує, що число блюд, що готуються, ненегативне. Клацнемо на кнопці ОК.

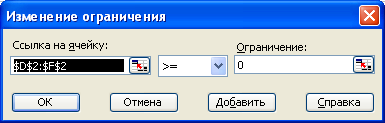
11. Знову клацнемо на кнопці Добавить. У полі Ссылка на клітину вкажемо діапазон D2: F2. Як умова виберемо пункт цел. Ця умова не дозволяє виробляти долі блюд. Клацнемо на кнопці ОК.

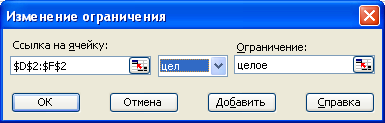
11. Клацнемо на кнопці Выполнить. Після закінчення оптимізації відкриється діалогове вікно Результаты поиска решения.

11. Встановимо перемикач Значення параметрів в положення Сохранить найденное решение, після чого клацнемо на кнопці ОК.

	Запас	Витрати	Блюдо А	Блюдо В	Блюдо С
			184	24	8	21600
Інгредієнт 1	5000	4960	20	50	10
Інгредієнт 2	4000	4000	20	0	40
Інгредієнт 3	4000	4000	20	10	10

Рис. 6. Результат обчислень з прикладу 3

В результаті вийде оптимальний набір змінних (оптимальна кількість фірмових блюд, що готуються) при даних обмеженнях (при даній кількості інгредієнтів): блюда А — 184 порції (x₁), блюда В — 24 порції (х₂) и блюда С — 8 порцій (x₃). При цьому загальна вартість блюд (Z) буде максимальною і рівною 21 600 крб. При цьому залишаться невитраченими 40 г пер­шого інгредієнта (рис. 6).

Проаналізуємо отримане рішення. Перевірити його оптимальність можна, експериментуючи із значеннями вічок D2: F2. Наприклад, допустимо, що вирішили приготувати кількість блюд, відповідно 184, 23, 9. Тоді при тій же загальній вартості блюд буде перевитрата другого інгредієнта на 40 г, що, природно, недопустимо. Можна розглянути і інші варіанти. Аби відновити оптимальні значення, можна у будь-який момент повторити операцію пошуку рішення.

Приклад 3.4 - приклад класу транспортні завдання (не обходжений знайти оптимальне рішення у вигляді двомірного масиву). Туристська фірма уклала контракт з двома турбазами: у м. Сухумі і в навколишніх містах, розрахованих, відповідно, на 200 і 150 чоловік.

Туристам для огляду пропонується мавпячий розплідник в місті, ботанічний сад і похід в гори. Складіть маршрут руху туристів так, щоб це обійшлось можливо дешевше, якщо:

• мавпячий розплідник приймає в день 70 чоловік, ботанічний сад — 180 чоловік, а в гори в один день можуть піти 110 чоловік;

• вартість одних відвідин виражається таблицею:

Турбаза	ОП	БС	Похід
1 2	5 10	6 12	20 5

Рішення. Для вирішення завдання введемо позначення: хай x₁₁, — число туристів з турбази в Сухумі, відвідуючих мавпячий розплідник; х₁₂ — число туристів з турбази в Сухумі, відвідуючих ботанічний сад; х₁₃ — число туристів з турбази в Сухумі, що вирушають в похід; x₂₁ — число туристів з навколишньої турбази, відвідуючих мавпячий розплідник; х₂₂ — число туристів з навколишньої турбази, відвідуючих ботанічний сад; х₂₃ — число туристів з навколишньої турбази, що вирушають в похід. Складемо цільову функцію — вона полягає в мінімізації вартості денних заходів турфірми: Z= 5 * x₁₁ + 6 * х₁₂ + 20 * х₁₃ + 10 * х₂₁ + 12 * х₂₂ + 5 * х₂₃.

Визначимо наявні обмеження (керуючись умовами завдання):

1. x₁₂+х₂₁70; (мавпячий розплідник приймає в день не більше 70 чоловік) ,

2. х₁₂ + x₂₂180; (ботанічний сад приймає в день не більш — 180 чоловік),

3. x₁₃ + x₂₃110; (у гори в один день можуть піти 110 чоловік)

4. х11 + х12 + х13 = 200; (відпочиваючих на турбазі в м. Сухумі 200 чоловік)

5. x₂₁ + x₂₂ + x₂₃=150. (відпочиваючих на турбазі в навколишніх містах 150 чоловік)

Крім того, оскільки турист неділимий і кількість туристів, що беруть участь в кожному заході, не може бути негативною, додамо ще ряд обмежень:

1) x₁₁  0;

2) х₁₂  0;

3) x₁₃  0;

4) x₂₁  0;

5. х₂₂  0;

6. x₂₃  0;

7. x₁₁ — ціле;

8. х₁₂ — ціле;

9. х₁₃ — ціле;

10. х₂₁ — ціле;

11. х₂₂ — ціле;

12. х₂₃ — ціле.

Тепер можна приступити до рішення задачі на комп'ютері.

1. Відкрийте новий робочий аркуш .

2. Складемо дві таблиці, в першій задамо вихідні дані, а в другій шукатимемо рішення:

	A	B	C	D	E	F
1		стоимость одного посещения
2	Турбаза	ОП	БС	Поход	кол-во отдыхающих
3	г. Сухуми	5	6	20	200
4	окресные	10	12	5	150
5	мах кло-во посетителей	70	180	110
6

• У клітини B5, C5 и D5 занесіть денну кількість відвідувачів різних заходів — числа 70, 180 и 110, відповідно.

• У клітини E3 і E4 занесіть кількість туристів в обох готелях — числа 200, и 150, відповідно.

• У клітини B3:D4 занесіть вартість одного відвідування (вихідні дані).

	A	B		C		D		E		F
8			кол-во участников
9	Турбаза		ОП		БС		Поход		кол-во участвующих в мероприятиях
10	г. Сухуми		0		0		0
11	окресные		0		0		0
12	кло-во посетителей
13	Затраты на посещение мероприятий

3. У клітини B10:D11 занесіть початкові значення невідомих х_11, х₁₂, ...,х₂₃ (нулі) — надалі значення цих вічок будуть підібрані автоматично.

6. У клітинах Е10:Е11 вкажіть формули для розрахунку обмежень (4,5). У клітині Е10 формула матиме вигляд =В10+С10+D10, а в Е11 формулу можна отримати методом автозаповнення (копіювання).

7. У клітинах В12: D12 вкажіть формули для розрахунку обмежень (1,2,3). У клітині В12 формула матиме вигляд =В10+В11, а останні формули в С12, D12 можна отримати методом автозаповнення (копіювання).

8. Для здобуття цільової функції потрібно порахувати витрати на кожен захід і заповнити клітини В13: D13. У клітині В13 формула матиме вигляд =В10*В3+В11*В4, а останні формули в С13, D13 можна отримати методом автозаповнення (копіювання).

9. У клітину Е13 занесемо формулу цільової функції підсумкові витрати на захід = В13+С13+D13.

10. Дайте команду Сервис ► Поиск решения — відкриється діалогове вікно Поиск решения.

11. У полі Установить целевую клітину вкажіть клітину , що містить значення, що оптимізується (Е13). Встановите перемикач Равной у положення мінімальному значенню (потрібний мінімальний об'єм витрат).

6. У полі Изменяя клітини задайте діапазон підбираємих параметрів (невідомих Xi) - B10:D11.

6. Аби почати визначати набір обмежень, клацніть на кнопці Добавить. У діалоговому вікні Додавання обмеження в полі Ссылка на клітину вкажіть діапазон В12: D12. Як умову задайте <=. У полі Ограничение задайте діапазон В5: D5. Ця умова вказує, що денна кількість відвідувачів заходів не повинна перевершувати їх можливостей. Клацніть на кнопці ОК.

7. Для продовження визначення набору обмежень клацніть на кнопці Добавить. У діалоговому вікні Добавление ограничения у полі Ссылка на клітину вкажіть діапазон Е10:Е11. Як умову задайте =. У полі Ограничение задайте діапазон Е3 : Е4 . Ця умова вказує, що денна кількість відвідувачів заходів має дорівнювати кількості туристів. Клацніть на кнопці ОК.

8. Знову клацніть на кнопці Добавить. У полі Ссылка на клітину вкажіть діапазон B10:D11. Як умову задайте >=. У полі Ограничение задайте число 0. Ця умова вказує, що число учасників заходів ненегативне. Клацніть на кнопці ОК.

9. Знову клацніть на кнопці Добавить. У полі Ссылка на клітину вкажіть діапазон B10:D11. Як умова виберіть пункт цел. Ця умова вказує, що турист неділимий. Клацніть на кнопці ОК.

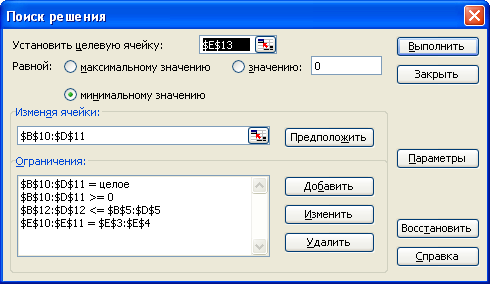
6. Клацніть на кнопці Выполнить. Після закінчення оптимізації відкриється діалогове вікно Результаты поиска решения.

7. Встановите перемикач Сохранить найденное решение, після чого клацніть на кнопці ОК.

	кол-во участников
Турбаза	ОП	БС	Поход	кол-во участвующих в мероприятиях
г. Сухуми	30	170	0	200
окресные	40	0	110	150
кло-во посетителей	70	170	110
выручка от посещения мероприятия	550	1020	550	2120

В результаті вийде оптимальний набір змінних (оптимальна кількість туристів для участі в кожному заході з кожного готелю) при даних обмеженнях (при заданих можливостях заходів): число туристів з турбази в Сухумі, відвідуючих мавпячий розплідник (х₁₁ = 30), ботанічний сад (х₁₂ = 170) і що вирушають в похід (х₁₃ = 0); число туристів з навколишньої турбази, відвідуючих мавпячий розплідник (х₂₁ = 40), відвідуючих ботанічний сад (x₂₂ = 0) і що вирушають в похід (х₂₃ = 110). При цьому сумарні витрати турфірми (Z) складуть 2120 крб. і будуть мінімальними.

Можна проаналізувати отримане рішення. Його оптимальність перевіряється шляхом експерименту із значеннями вхідних даних. Аби відновити оптималь­ні значення, можна у будь-який момент повторити операцію пошуку рішення.

Іншими типовими прикладами транспортних задач лінійного програмування є задачі:

1. Про раціон живлення.

2. Про оптимальні перевезення.

3. Про оптимальний план пошивочної майстерні.

4. Про раціональне використання сировини.