Оценка энергетического состава -квантов по функциям пропускания

Ранее было показано, что в условиях «хорошей» геометрии ослабление моноэнергетического пучка -квантов каким-либо материалом можно записать в следующем виде:

,

где n₀ – количество регистрируемых квантов при t = 0; п(t) – количество регистрируемых квантов после их прохождения через материал толщиной t. Отношение п(t)/n₀ = Т(t) называют функцией пропускания.

В логарифмическом масштабе функция пропускания – прямая линия, тангенс угла наклона которой равен коэффициенту ослабления -квантов , зависящему от энергии -квантов. Эта зависимость для различных материалов известна с точностью около 1…2%. Таким образом, измерив функцию пропускания, можно определить и по известной зависимости (E) определить энергию -квантов.

В случае, если исследуемое излучение является моноэнерге­тическим, можно измерить наклон функции пропускания с хоро­шей точностью, а точность определения энергии будет зависеть от того, насколько велика производная dμ/dE. Следует отметить, что функция μ(Е) в материалах со средними и большими атомными номерами имеет минимум, и поэтому разные энергии -квантов могут иметь одинаковые значения μ. Кроме того, поскольку минимум функции μ(Е) не резкий, то в этой области энергий точность определения энергий -квантов небольшая. Эти затруднения не принципиальны, так как всегда можно измерить функции пропускания для элементов с малым атомным номером, для которых этот минимум смещен в область высоких энергий -квантов.

Например, в алюминии минимум находится при энергии -квантов около 20 МэB, а в углероде – примерно при 50 МэB.

Существенным источником ошибок при определении энергии -квантов по функциям пропускания может быть недостаточно хорошая геометрия опытов, при которой ослабление излучения отличается от приведенного выше закона. Напомним, что этот закон получен в предположении, что каждое взаимодействие -кванта выводит его из пучка. В реальном случае всегда имеется конечная вероятность того, что -квант провзаимодействует в поглотителе не один раз и попадет после двух или более взаимодействий в детектор. Пути таких квантов показаны на рис. 10.1.

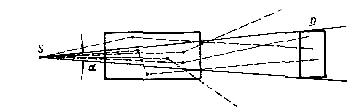
Рис. 10.1. Определение энергии γ-квантов по функциям пропусканияъ

Вклад таких процессов зависит главным образом от геометрии опыта и диаметра поглотителя. Для проведения корректных измерений функций пропускания необходимо, чтобы угол расхождения пучка -квантов не превышал 1° (угол α на рис. 10.1).

Оценим точность, с которой можно определить энергию моноэнергетического пучка -квантов по функциям пропускания, считая известной зависимость (E) с точностью 1% и полагая (Е) ~ 1/Е.

Можно показать, что

,

где /T– относительная ошибка измерения ослабления пучка -квантов. При Т = 10^-2 необходимо измерить ослабление пучка -квантов с точностью до 5·10^-2 для определения энергии монохроматического пучка -квантов с точностью, с которой известна зависимость (Е), т.е. 1%.

В случае немоноэнергетического излучения функция пропускания имеет сложный вид, и по ее форме можно лишь сделать оценки энергетического состава -излучения.

Хотя приложения метода пропускания оказываются весьма ограниченными, представляет интерес оценить энергетическое разрешение метода для случая, когда спектр содержит две группы -квантов с близкими энергиями Е₁ и E₂ и одинаковыми (или близкими) интенсивностями. Вычислим, с какой точностью необходимо измерить функции пропускания для установления по форме кривой пропускания наличия двух групп -квантов. Пусть относительная точность измерения числа отсчетов за толщинами поглотителя t есть и пусть измеряются скорости счета п₀. n₁ и п₂ за толщинами поглотителя t = 0, t = t₁, и t = t₂. Уверенно судить о наличии двух групп -квантов по измеренным величинам п₀, п₁ и п₂ можно в том случае, если эти величины в зависимости от t не лежат на одной экспоненте с учетом ошибок измерения . Предполагая t₂ = 2t₁ это условие можно записать следующим образом:

.

Зависимость скорости счета п(t) для двух групп -квантов одинаковой интенсивности запишем в виде

,

где и – коэффициенты линейного ослабления -квантов с энергиями е₁ и Е₂ соответственно. Если считать, что >> , то условие разделения двух групп -квантов примет вид

.

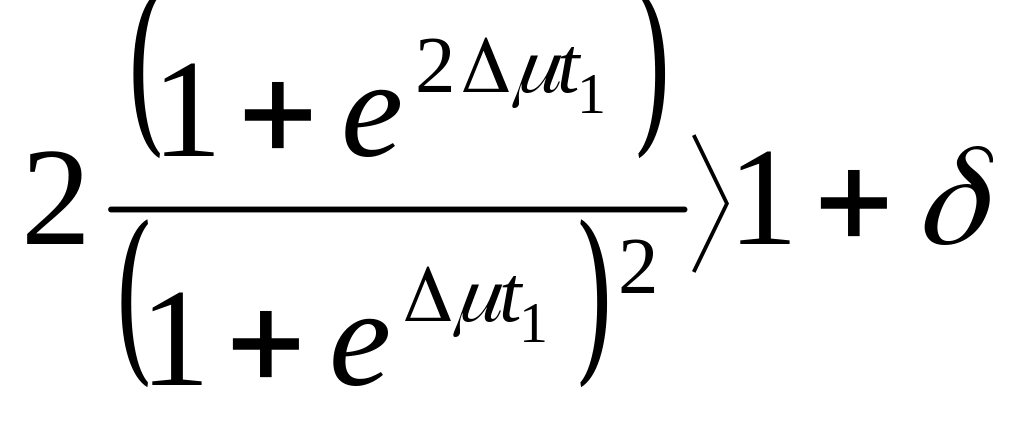Таким образом, проделав все вычисления, при ≈ 0,05 ΔЕ/Е ≈ 0,15/ , где ΔE – минимальное отличие в энергиях двух групп -квантов, которое можно заметить при оговоренных выше условиях.

Проведенная оценка показывает, что для разрешения двух групп - квантов, отличающихся по энергии на 5%, необходимы ослабления излучения при t = t₂ приблизительно в 400 раз при 0,05, а при 0,015 – всего в 30 раз. Светосила этого метода невелика и по порядку величин равна /4. При 1° и величина L ≈ 0,5^.10^-6.