Переходы в полупроводниках

Работа всех существующих полупроводниковых детекторов основана на использовании свойств перехода между полупроводниками с разным типом проводимости. На рис. 3.5 изображен р–n-переход, причем число донорных примесей в образце больше, чем число акцепторов в p-образце.

Сами ионизированные атомы акцепторов и доноров закреплены в решетке и двигаться не могут, но носители при Т > 0 ^оК могут диффундировать, если существует градиент концентрации носителей данного знака. Диффузия, как дырок, так и электронов вызывает протекание электрического тока из p-области в n-область. При отсутствии источника внешнего напряжения, приложенного к р-n-переходу, после установления равновесия ток прекращается из-за появления на переходе скачка потенциала, который возникает из-за существования объемного заряда в области контакта полупроводников с разными свойствами. Не скомпенсированный свободными основными носителями положительный заряд доноров будет равен не скомпенсированному отрицательному заряду акцепторов. Высота потенциальной ступеньки зависит от числа и диффузионной способности носителей, которые, в свою очередь, являются функциями температуры, числа примесей и т.д. Величина скачка потенциала может достичь нескольких десятых долей вольта, но не может быть больше, чем ширина запрещенной зоны, в случае, если полупроводники с разными типами проводимости изготовлены из одного материала, например кремния.

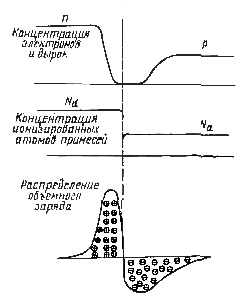
Рис. 3.5. Равновесный р – n-переход

В материале n-типа всегда присутствуют дырки, а в материале p-типа – электроны, созданные тепловыми переходами через запрещенную зону. В нашем примере более сильного легирования п материала плотность не основных носителей (электронов) в p-области много больше плотности не основных носителей (дырок) в п-области. В состоянии равновесия осуществляется баланс для числа носителей каждого знака, пересекающих переход в обоих направлениях. Для нашего случая значения электронного тока больше дырочного (по абсолютному значению эти токи достигают многих ампер).

Полупроводник с р-n-переходом может использоваться для детектирования заряженных частиц даже при отсутствии внешнего источника напряжения, поскольку внутри такого полупроводника существует область, в которой напряженность электрического поля отлична от нуля. Если через эту область пролетает заряженная частица и создает свободные носители, то они, перемещаясь под действием электрического поля, создадут сигнал во внешней цепи детектора. Однако ширина области объемного заряда в р-n-переходе без внешнего смещения мала (<10^-4 см), что приводит, во-первых, к малому чувствительному объему детектора, и, во-вторых, к .малой величине сигнала по сравнению с шумом, так как собственная емкость перехода велика. Чувствительную область детектора, т.е. область, в которой существует электрическое поле, можно увеличить, прикладывая к переходу обратное смещение, т.е. к n-области присоединить плюс источника напряжения, а к p-области – минус. Обратное смещение помогает напряжению, возникшему на р-n-переходе, удалять свободные носители из области вблизи перехода. В результате чувствительный объем детектора, т.е. объем обедненного носителями слоя, в котором существует электрическое поле, увеличивается, а емкость перехода уменьшается. Рассмотрим свойства р-п-перехода с обратным смещением (рис. 3.6), причем n-область сильно легирована, а p-область – слабо. Свободные носители «выметены» электрическим полем из обедненной области толщиной d, и дипольный слой состоит почти полностью из закрепленных ионизированных доноров и акцепторов.

Почти полное отсутствие свободных носителей в обедненной области означает, что удельное сопротивление материала в ней гораздо больше, чем удельное сопротивление полупроводника, вне перехода. Высокое удельное сопротивление материала – основное условие работы полупроводникового детектора.

На рис. 3.6 показаны также распределения потенциала и напряженности электрического поля в переходе. Изображены они с резкими границами, что, конечно, условно, поскольку реально плотность носителей, а соответственно и все остальные величины, изменяются плавно.

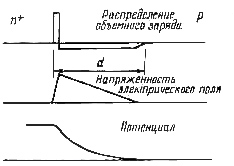
Рис. 3.6. Распределения потенциала и напряженности электрического поля в переходе: p– n - переход с обратным смещением

По порядку величины плотность свободных носителей в области перехода меньше плотности вне перехода в отношении Δt/τ, где Δt – среднее время нахождения носителя в области перехода; τ – время жизни носителей относительно рекомбинации в отсутствие напряжения смещения. Величина Δt – время, за которое носитель выметается электрическим полем из перехода, – уменьшается при увеличении смещения на переходе. При больших обратных смещениях (соответствующих реальным) можно предполагать при расчетах, что в слое объемного заряда совсем нет свободных носителей.

Ширина обедненной зоны. В случае сильного легирования n – области все приложенное напряжение смещения падает на p-область, поскольку ее сопротивление больше (приблизительно N_d/N_a раз). Такая ситуация характерна для полупроводниковых детекторов, и в этом случае ширина обедненной зоны

,

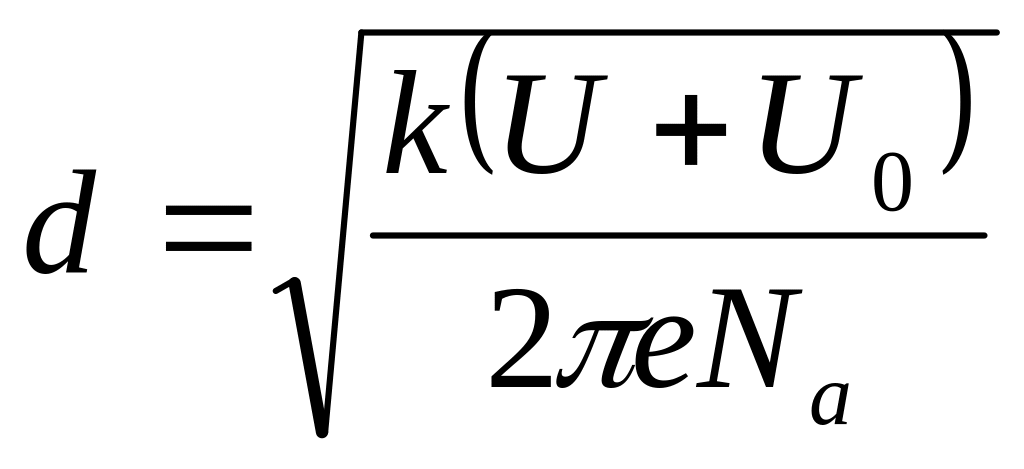где k – диэлектрическая постоянная полупроводника; N_a – плотность электрически активных центров в слаболегированной области. Если в полупроводнике р-типа есть и донорные уровни, то N_a – разность между концентрациями доноров и акцепторов; U – напряжение смещения; U_o – скачок потенциала на переходе; U₀ 0,7 B для Si и U₀ 0,3 B для Ge. Число основных носителей для неохлажденного примесного полупроводника приближенно равно числу атомов примеси (N_a в нашем примере), следовательно, ширину обедненной зоны можно выразить через удельное сопротивление и подвижность основных носителей слаболегированного материала. Учитывая, что всегда U > Uо, и для оценки считая подвижность постоянной, получаем приближенное выражение для ширины обедненной зоны d. Для кремния

,

где ρ – в ком·см, U – в B для U = 500 B и ρ – 20 ком·см, а именно таким сопротивлением обладают лучшие образцы р-кремния, находим d = 0,13 см.

Показательно, что для получения чувствительной области глубиной 0,1 см и площадью 1 см² с однородным счетчиком при хорошем отношении сигнала к шуму нужен был бы полупроводник с удельным сопротивлением, равным примерно 10⁹ Oм·см. Величина максимальной напряженности электрического поля в переходе такого типа дается выражением

.

Эта величина интересна по двум причинам. Если Е_макс достигает значений, больших 2^.10⁴ B/см, то возможно возникновение вторичной ионизации. Кроме того, если скорость дрейфа носителей, равная произведению E·μ, достигает значений, сравнимых с тепловой скоростью электронов в решетке (~10⁷ см/с), то она перестает зависеть от напряженности электрического поля. Этот эффект может оказаться важным, при оценке времени собирания носителей.

Емкость р-n-перехода. Если заряженная частица проходит через р-n-переход, то в слое образуется некоторый заряд.

Величина импульса, возникшего на р-n-переходе после сбора носителей, обратно пропорциональна сумме емкости перехода и входной емкости регистрирующего устройства. Отношение сигнал/шум для такой системы уменьшается, если емкость перехода растет. Переход с обратным смещением приближенно может рассматриваться как изолятор с металлическими электродами.

Для кремния , для германия , т.е. для детектора с s = 1 см² и d = 0,02 см собственная емкость пере­хода достигает 50...70 пФ.

Токи утечки через переход. Поскольку проводимость переходной области, к которой приложено напряжение смещения, отлична от нуля, то через переход будет постоянно протекать ток. При анализе работы полупроводниковых детекторов этот ток принято называть током утечки.

Минимальная величина сигнала, который еще можно отделить от сигналов шума, а также энергетическое разрешение при измерении энергий частиц зависят от флуктуации токов утечки, которые по абсолютной величине тем больше, чем больше сам ток.

Токи утечки условно можно разделить на объемные и поверхностные компоненты.

Проведем численную оценку объемных токов утечки: диффузионного i_d и тока генерации i_g. Сначала рассмотрим диффузионный ток. Он возникает в р-n-переходе по двум причинам:

1) не основные носители (дырки) в n-области диффундируют к краю обедненной носителями области объемного заряда и подхватываются электрическим полем в этой области;

2) электроны в p-области диффундируют к переходной области и тоже подхватываются электрическим полем и переносятся в р-область.

В нашем примере высоколегированной n-области определяющей является диффузия электронов из p-области. Оценим ее, помня, что все рассуждения верны и для дырок из n-области. Электроны в p-области возникают в результате тепловой генерации. Для оценки существен объем полупроводника, находящийся на расстоянии длины диффузии носителей L_n от области, в которой существует градиент электрического поля, следовательно, объем генерации носителей равен L_n·s, где s – площадь перехода. В состоянии равновесия (при отсутствии внешнего электрического поля) этот объем содержит s·L_n·n_p электронов, где п_р – плотность, электронов в p-области. Каждый электрон, в среднем, существует τ_г с, следовательно, число рекомбинаций в 1 с в этом объеме равно (s·b_n·n_p)/i_r, а исчезающий в 1 с заряд – (s·L_n·n_p·e)/τ_r. Для получения верхней оценки диффузионного тока утечки через переход предположим, что все электроны, созданные в рассматриваемом объеме вблизи перехода, попали в область, где существует электрическое поле, тогда диффузионный ток i_d

.

Выразим i_d через характеристики полупроводника: сопротивление, подвижность и число собственных носителей. Для полупроводника p-типа удельное сопротивление

,

где p – плотность основных носителей в р-области. Длина диффузии связана с коэффициентом диффузии D и временем жизни носителей соотношением . Величина D, в свою очередь, связана с температурой и подвижностью носителей формулой Эйнштейна

.

Учитывая также, что п_р·р = , получаем

.

Как и следовало ожидать, ток диффузии не зависит от обратного смещения на переходе, а определяется только свойствами материала. Подставляя значения постоянных, для кремния при комнатной температуре находим для плотности тока j = i_g/s

a/см.

В этой формуле р_л выражено в ком·см, – в мкс.

Для типичного кремниевого детектора с р-n-переходом = 1 ком·см, = 50 мкс, т.е. j_a = 2,3·10^-9 а/см². Для германиевого детектора при комнатной температуре диффузионный ток был бы очень велик, и, в частности, поэтому они при комнатной температуре не применяются.

Для детекторов с большой глубиной чувствительной области d важным источником токов утечки становится тепловая генерация (j_g – ток генерации) носителей в области перехода. Носители, возникшие здесь, практически все выметаются электрическим полем из зоны перехода, не успевая рекомбинировать в ней.

Число возникающих в обедненной зоне носителей пропорционально объему зоны, умноженному на вероятность образования пары носителей за счет теплового переброса электрона из валентной зоны в зону проводимости.

Во многих случаях основной вклад в величину тока утечки вносят поверхностные токи, величина которых зависит от свойств боковых поверхностей кристалла, их чистоты и качества обработки. Ток утечки возрастает пропорционально напряжению смещения. Рассчитать величину поверхностного тока практически невозможно. Чтобы уменьшить ток утечки, иногда полупроводниковые детекторы помещают в вакуум. Применяются и охранные кольца, которые значительно уменьшают этот ток.

Кроме р-n-перехода существует еще один тип перехода, также используемый в детекторах. Это так называемый поверхностно-барьерный переход. Некоторые металлы, такие, как золото, будучи нанесены испарением па поверхность германия или кремния n-типа, создают переход, во многом подобный истинным р-n-переходам. Распространенный способ изготовления поверхностно-барьерных счетчиков – создание переходного слоя при окислении специальным образом обработанной поверхности кремния кислородом воздуха. От способов изготовления транзисторов этот метод отличается лишь более высокой температурой и более длительным временем диффузии, что необходимо при создании толстого перехода. Для типичных значений удельного сопротивления кремния 10²…10⁴ Oм·см и обратного смещения 200…300 B толщины обедненного слоя достигают значений 500…1000 мкм. Такие толщины достаточны для измерения осколков деления, β-частиц с энергией до 500 кэB, α-частиц из естественных источников и ускоренных протонов малых энергий.

Поскольку толщина обедненного слоя мала, то емкость таких поверхностно-барьерных детекторов велика, что в свою очередь ограничивает достижимое энергетическое разрешение.

Bеличину d можно увеличить двумя способами: поднимая напряжение смещения U и уменьшая число примесных атомов, т.е. увеличивая сопротивление материала. Если образец достаточно толстый, то увеличение U действительно приводит к росту толщины обедненного слоя, который может раздвинуться почти до металлических контактов, присоединенных к детектору. Однако в этом случае электрическое поле вытягивает электроны из металла и через полупроводник течет очень большой ток, называемый током инжекции. Этот ток инжекции из контак­тов остается очень значительным, даже если область перехода и не достигает их. Поэтому при создании детекторов с большим d в качестве контактов используют высоколегированные полупроводники. Такие детекторы называют обычно, хотя и не очень точно, детекторами с р-i-n-переходом, а более точно, если основной материал детектора с дырочной проводимостью, это детекторы с п⁺-р-р⁺-переходом (знак «плюс» означает сильное легирование). Видно, что основное изменение потенциала происходит в р-области и электрическое поле возникает почти по всей глубине образца. Такой переход изображен на рис. 3.7.

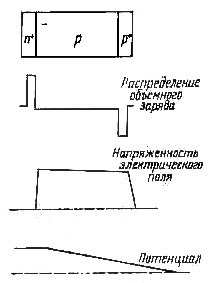
Рис. 3.7. Упрощенное изображение распределения объемного заряда, напряженности электрического поля и потенциала на переходе: p- i- n – переход с обратным смещением

Для получения большого значения d сопротивление слабо легированной р-области должно быть как можно больше, т.е. число некомпенсированных примесных атомов N_a в этой области минимально. Компенсация акцепторных примесей в р-полупроводнике осуществляется с помощью дрейфа лития, являющегося донором.

Свойства лития, внедренного в германий или кремний, таковы, что позволяют создавать достаточно большие области (толщиной > 1 см) почти полной компенсации, а значит и области с проводимостью, близкой к собственной. Это связано, как с исключительно высокой подвижностью ионов лития в четырехвалентных кристаллах, так и с низкой энергией его ионизации (0,033 эВ в Si и 0,0043 эВ в Ge). Например, подвижность, а, следовательно, и коэффициент диффузии лития в германии в 10⁷ раз больше, чем у обычных доноров, так как благодаря своему малому радиусу ион лития может находиться не в узлах решетки, а в междоузлиях.

Компенсация акцепторных атомов в р-материале с помощью дрейфа лития производится следующим образом. Сначала литий напыляется на р-материал, затем температура поднимается примерно до 400 °С, и литий диффундирует внутрь образца. Диффузия продолжается несколько минут, и литий диффундирует на глубину примерно 0,01 см. После этого к р-n-переходу прикладывается обратное смещение и ионы лития, которые несут положительный заряд, начинают двигаться от n-стороны перехода к р-стороне, где они компенсируют акцепторные атомы р-материала.

Расчеты дают следующую формулу для толщины полученного в результате дрейфа обедненного слоя:

,

где μ_Li подвижность ионов Li в данном полупроводнике при температуре дрейфа; U – напряжение смещения при дрейфе; t – время дрейфа.

Для оценки объемных токов утечки через р-i-n-переход и его емкости могут быть использованы формулы, полученные ранее для р-i-n-перехода.

Как уже упоминалось, работа с литий-дрейфовыми детекторами из германия требует охлаждения их до температуры жидкого азота, а значит, и сложной криостатной установки, обеспечивающей не только низкую температуру, но и возможность входа исследуемых частиц в детектор.

Энергетическое разрешение. В спектрометрии ядерных излучений с полупроводниковыми детекторами мерой энергии, оставленной заряженной частицей в чувствительном объеме, является амплитуда сигнала во внешней цепи детектора. При облучении детектора пучком заряженных частиц, разброс по энергии которых пренебрежимо мал и пробег которых полностью укладывается в чувствительном объеме детектора, амплитуды сигналов во внешней цепи будут иметь некоторый разброс вокруг среднего значения. Величина этого разброса и определяет энергетическое разрешение детектора. Как показывает опыт, с достаточно хорошей точностью распределение сигналов по амплитудам (или иначе, амплитудное распределение импульсов) можно описать распределением Гаусса, а в качестве меры разброса использовать среднеквадратичное отклонение а. На практике за меру разброса амплитуд импульсов принимают ширину распределения на полувысоте. В случае распределения Гаусса она равна 2,3 .

Полупроводниковые детекторы характеризуются весьма малыми значениями (< 0,01). Дисперсия амплитудного распределения ² складывается из ряда членов, обусловленных как самой природой процессов в счетчике, так и внешними причинами, например шумами усилителя.

Предположим также, что толщина мертвого слоя на поверхности счетчика, через который заряженные частицы попадают в детектор, пренебрежимо мала. Примем, что постоянная времени входной цепи усилителя сигналов много больше времени сбора носителей в детекторе. Последние два ограничения не принципиальны и могут быть учтены при некотором усложнении расчетов.

Каждый источник разброса амплитуд сигналов будем характеризовать дисперсией D_i или среднеквадратичным отклонением σ_i. Будем считать, что амплитудное распределение описывается распределением Гаусса с . При рассмотрении полупроводниковых счетчиков часто среднеквадратичное отклонение распределения или _i выражают в энергетических единицах, считая его равным энергии частицы, образующей сигнал, равный по величине среднеквадратичному отклонению, т.е. ^Е=W· .

Флуктуации числа образованных пар носителей. При отсутствии потерь носителей при их движении к электродам среднее число собранных пар N =E/W, где Е – энергия частицы. Если бы процесс образования пар носителей описывался распределением Пуассона, то σ_с (статистическое) было бы равно (E/W)^½. Однако в полупроводнике заметная часть (около 30%) энергии частицы идет на образование носителей, и поэтому процесс не описывается распределением Пуассона. Отклонение от этого распределения учитывается множителем F и тогда

σ_с =W(FE/W)^½.

Для германия и кремния величина F по разным оценкам лежит в интервале 0,1…0,3.

Например, для кремниевого детектора с W = 3,65 эв, предполагая, что Е=1 Мэв, получаем в энергетических единицах σ_с ~ 1 кэв.

Это соотношение определяет принципиальный предел энергетического разрешения полупроводникового счетчика.