4.5.2. Основные типы ппд Характеристики кремния и германия

Кремний и германий – четырехвалентные элементы с простой структурой (8 атомов в элементарной ячейке) и ковалентными связями, полностью насыщенными при низких температурах. При повышении температуры часть ковалентных (двойных) связей разрывается, что ведет к образованию электронно-дырочных пар. Число пар собственных носителей в собственном полупроводнике п_i следующим образом зависит от температуры Т и ширины зоны:

где b – const данного материала; Т – температура по шкале Кельвина.

Величина тока в полупроводнике, созданная дрейфующими под действием поля носителями, определяет удельное сопротивление полупроводника ρ. Из определения ρ как величины обратной проводимости σ следует, что

где μ⁺, μ^– – подвижности носителей; р, п – объемные плотности положительных и отрицательных носителей.

Некоторые характеристики чистых (беспримесных) кремния и германия приведены в табл. 3.1.

Из таблицы видно, что ширины запрещенных зон кремния и германия отличаются меньше чем в два раза, а число носителей – на три порядка. Это связано с экспоненциальной зависимостью числа носителей от ширины запрещенной зоны. Подвижности носителей близки по величине и, что очень важно для спектрометрических измерений, подвижности электронов и дырок – одного порядка и в германии, и в кремнии. Видно, что если полупроводник охладить, то подвижности резко возрастут, а следовательно, улучшатся временные характеристики детектора. Уменьшение μ⁺ и μ^– с ростом Т объясняется увеличением сечения неупругих столкновений носителей с решеткой.

Таблица 3.1. Физические характеристики кремния и германия

Характеристика	Si	Ge
Атомный номер Атомная масса Плотность при 300 оК, г ¤см3 Диэлектрическая постоянная Ширина щели при 300 оК, эВ Энергия ионизации, эВ Плотность собственных носителей при 300 оК, см – 3 Подвижность электронов при 300 оК, см3/(В×с) Подвижность дырок при 300 оК, см3/(В×с) Подвижность электронов при 77 оК, см3/(В×с) Подвижность дырок при 77 оК, см3/(В×с) Собственное удельное сопротивление при 300 оК, Ом×см Собственное удельное сопротивление при 77 оК, Ом×см	14 28,06 2,33 12 1,106 3,66 1,5×1010 1350 480 4×104 1,8×104 3×105 -	32 72,60 5,33 16 0,67 2,96 2,4×1013 3900 1900 3,6×104 4,2×104 50 5×104

Используя характеристики германия и кремния, приведенные в табл. 3.1, получаем при Т = 300 °К для беспримесных полупроводников численные значения удельного сопротивления:

Ом·см, =230·10³ Ом·см.

Видно, что сопротивление очень быстро растет с уменьшением температуры. При Т = 77 °К собственная проводимость и кремния, и германия падает настолько, что (при отсутствии примесных уровней) они являются превосходными изоляторами и, следовательно, их можно использовать для изготовления однородных полупроводниковых счетчиков.

Свойства примесных германия и кремния. Если для германия еще и можно достичь такой степени очистки от электрически активных примесей (<10¹³ атом/см³, т.е. <5·10^-6%), при которой свойства при комнатной температуре в основном будут определяться характеристиками собственно германия, то для кремния (допустимое количество примесей ~ 5·10^-9%) это пока невозможно. Следовательно, полупроводниковый материал, используемый для изготовления детекторов, почти всегда будет примесный, причем тип примеси зависит от свойств материала и технологии изготовления. Так, из кремния особенно трудно удалять бор, поэтому кремний с наиболее высоким удельным сопротивлением – это р-кремний (бор – акцептор). Германий очень сложно очищать от кислорода. Поскольку содержание загрязнений трудно контролировать, примеси обычно вводят искусственно, используя для этого или пятивалентные (фосфор, мышьяк), или трехвалентные атомы (бор, алюминий). В первом случае в решетке появляется слабо связанный «лишний» электрон (донорный уровень), связь которого при комнатной температуре разорвана, во втором электрона не хватает, появляется дырка (акцепторный уровень). Некоторые примеси (например, золото) могут вносить одновременно и донорные и акцепторные уровни, расположенные приблизительно в середине запрещенной зоны.

В полупроводнике с собственной проводимостью число дырок в валентной зоне и число электронов в зоне проводимости равно п_i. Это результат равновесия между процессами рекомбинации и генерации носителей. Скорость рекомбинации и генерации существенно повышается, если появляются дополнительные уровни в запрещенной зоне, поскольку скорость двухступенчатых переходов больше, чем одноступенчатых. Но, несмотря на возрастание скорости процессов, суммарное число носителей в равновесном полупроводнике не возрастает, т.е. выполняется соотношение

,

где п – число электронов в 1 см³; р –число дырок в 1 см³ в примесном полупроводнике; n_i – концентрация электронов или дырок в беспримесном полупроводнике (n _t= f(T) – функция температуры).

Эта формула следует из выражений для числа электронов и дырок в невырожденном полупроводнике, подсчитанных по зонной теории. Следовательно, увеличение числа электронов в зоне проводимости при введении донорных примесей приводит к уменьшению числа дырок. Так, если в кремний при комнатной температуре ввести 1,5·10¹¹ донорных атомов на 1 см³, т.е. всего один атом примеси на 4·10¹⁰ атомов кремния, то плотность дырок будет 1,5·10⁹, т.е. в 10² раз меньше электронной. Удельное сопротивление образца будет определяться только электронами и составит около 3,5·10³ ом·см, т.е. почти на два порядка меньше собственного при этой же температуре. Лучшая очистка зонной плавкой позволяет получать р-кремний с сопротивлением около 10⁴ ом·см. Т.о. минимальное число свободных носителей обоих знаков будет при п = р независимо от того, является ли это равенство результатом отсутствия всяких примесей или следствием того, что число донорных примесных атомов равно числу акцепторов. Последнее обстоятельство используют на практике при создании полупроводников с высоким удельным сопротивлением. Энергетическая схема полупроводника, у которого концентрация донорных примесей N_d равна концентрации акцепторных примесей N_a,, изображена на рис. 3.4.

У такого полностью компенсированного полупроводника проводимость равна проводимости беспримесного полупроводника.

При высоких температурах (около 420 °К для очень чистого кремния и около 330 °К для очень чистого германия) величина n_i возрастает настолько, что при любом количестве примесных атомов (10¹²…10¹⁶ атом/см³) сопротивление определяется собственными (непримесными) носителями. При понижении температуры определяющими становятся примесные носители вплоть до температур (10…50 °К), при которых примесные атомы перестают быть ионизированными.

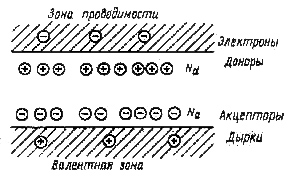
Рис. 3.4. Компенсированный полупроводник с полностью ионизированными атомами примеси* N_d и N_a – концентрации доноров и акцепторов