Энергетическое разрешение

Энергетическое разрешение камер в конечном счете определяется флуктуацией в числе образуемых заряженной частицей пар ионов и составляет

где F – фактор Фано, равный примерно 0,7 для рассматриваемого случаи;

п – число пар ионов.

Такой величины η можно достигнуть в том случае, если пробеги всех частиц укладываются в рабочем объеме камеры (отсутствует стеночный эффект), камера работает в режиме полного собирания (нет индукционного эффекта), малы амплитуды шумов усилителя, все частицы, попавшие в камеру, имеют одинаковую энергию. Минимальная величина η составляет примерно 3% при энергии заряженной частицы 0,1 МэВ и около 0,4 % при энергии 5 Мэв.

В некоторых случаях, действительно, удается полностью избавиться от стеночного (источник помещен внутрь камеры на рас­стояниях от ее стенок, больших, чем пробеги заряженных частиц) и индукционного эффектов (плоская камера с сеткой, большие величины постоянной RC, и тогда получают величины η, близкие к расчетным. Так, в камерах с сеткой получено энергетическое разрешение для α-частиц с энергией 5 Мэв, равное 0,5%. При измерениях энергии частиц, которые образуются в результате взаимодействия нейтронов и γ-квантов с ядрами газа, наполняющего камеру, стеночным эффектом, как правило, пренебречь нельзя, и он приводит к увеличению величины η. Следует отметить, что для полного избавления от индукционного эффекта необходимо RC ~ 10^-3 с, а это означает, что детектор будет обладать плохими временными характеристиками. В цилиндрических и сферических камерах возможно выбирать меньшие значения RC, допуская незначительное увеличение η за счет индукционного эффекта.

Эффективность регистрации

Ионизационные камеры регистрируют заряженные частицы, попавшие в рабочий объем камеры, со 100%-ной эффективностью, если амплитуда импульса превышает порог регистрирующего устройства. Несколько сложнее определить эффективность, когда ионизационные камеры используются для регистрации γ-квантов и нейтронов. Гамма-кванты можно зарегистрировать в камере по электронам, образующимся в результате рассеяния и поглощения γ-квантов. Пробеги электронов в газе велики (средний пробег электрона с энергией 0,5 Мэв в воздухе при нормальных условиях составляет около 1,5 м), и поэтому камеры практически не используют для определения энергии γ-квантов по электронам отдачи. При регистрации γ-квантов чаще используют камеры в токовом режиме, где при определенных условиях ток оказывается пропорциональным энер­гии, поглощаемой в стенках камеры. При расчете эффективности основная сложность в опре­делении числа электронов, попадающих в рабочий объем камеры из ее стенок. Число электронов отдачи, которое образуется при взаимодействии γ-квантов с атомами газа, наполняющего камеру, обычно гораздо меньше.

Методы регистрации с газовым усилением

4.3.4.Пропорциональные счетчики

При достаточно высокой напряженности поля, дрейфующие к аноду электроны между соударениями, могут приобрести энергию, достаточную для ионизации молекул газа. Такие условия приводят к увеличению тока или амплитуды импульсов. Это явление увеличение числа электронов за счет вторичной ионизации – носит название газового усиления. На рис. 2.6 показаны амплитуды импульсов в цилиндрическом счетчике в зависимости от приложенного напряжении для двух различающихся в 10 раз начальных ионизаций.

Видно, что в области 2 амплитуды импульсов вырастают в 10…100 раз и при этом сохраняется пропорциональность между величинами импульсов и начальной ионизацией. Эту область называют областью работы пропорционального счетчика. При дальнейшем увеличении напряжения пропорциональность нарушается, а затем амплитуда импульса оказывается независящей от первичной ионизации. Рассмотрим механизм газового усиления и дадим качественные объяснения поведения вольтамперной характеристики.

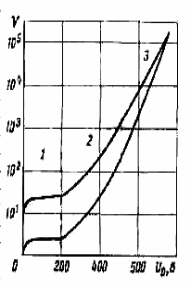
Рис. 2.6. Зависимость амплитуды импульса от напряжения U_n: 1 – область работы камеры, 2 – область работы пропорционального счетчика, 3 – область ограниченной пропорциональности.

Механизм газового усиления

Для осуществления вторичной ионизации необходимо, чтобы между столкновениями электрон приобрел энергию, достаточную для ионизации атомов, молекул газа. Считая, что электрон приобретает необходимую для вторичной ионизации энергию между двумя столкновениями, оценим напряженность электрического поля. Например, средний свободный пробег электрона между соударениями в водороде при давлении примерно 100 мм рт. ст. около 10^-3 см. Чтобы происходила ионизация атомов водорода, необходима энергия выше 15 эв. Таким образом, в рассматриваемом примере для вторичной ионизации необходимо электрическое поле напряженностью выше 1,5·10⁴ в/см. Такое поле при сравнительно низких приложенных напряжениях можно получить в цилиндрических счетчиках с тонкой центральной нитью. При этом необходимая напряженность будет получена вблизи центрального электрода. Здесь первичные электроны могут образовать вторичные электроны, которые, в свою очередь, приобретут энергию, достаточную для ионизации, и т.д. Это приведет к процессу размножения электронов и созданию электронно-ионной лавины.

Оценим, какова вероятность ионизации на единице пути. Пусть взаимодействие электронов с атомами характеризуется полным сечением взаимодействия σ_t, а вероятность ионизации – сечением ионизации σ_ион. Для того чтобы был возможен процесс вторичной ионизации, электрон должен приобрести энергию выше потенциала ионизации I_ион. Такую энергию электрон может приобрести в электрическом поле Е, если пройдет путь без соударений х ≥ λ = I_ион/e·E. Вероятность электрону пройти путь х и ионизовать атом на пути dx равна σ_ион·N·ехр(-x·N·σ_t)dx. Интегрируя по х от λ, (при х < λ, энергия электрона еще мала для вторичной ионизации) до ∞, получаем вероятность вторичной ионизации при пробеге электроном пути, большего λ:

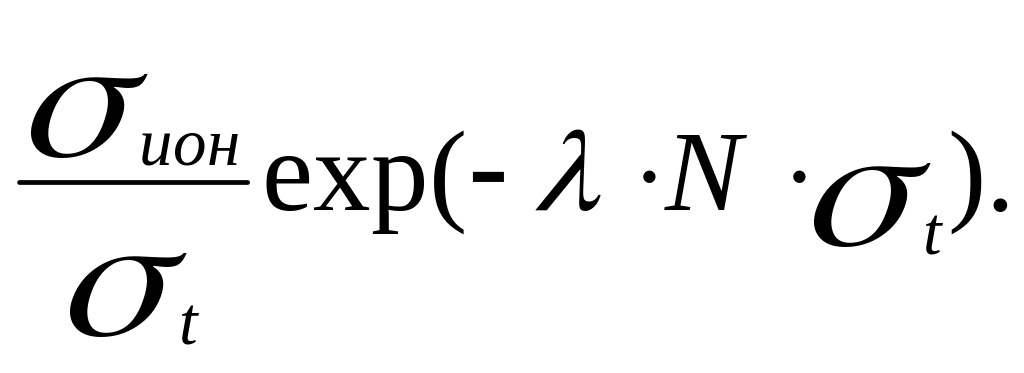
Учитывая, что средний свободный пробег электрона между соударениями равен 1/Nσ_t, находим вероятность вторичной ионизации на 1 см пути или макроскопическое сечение вторичной ионизации:

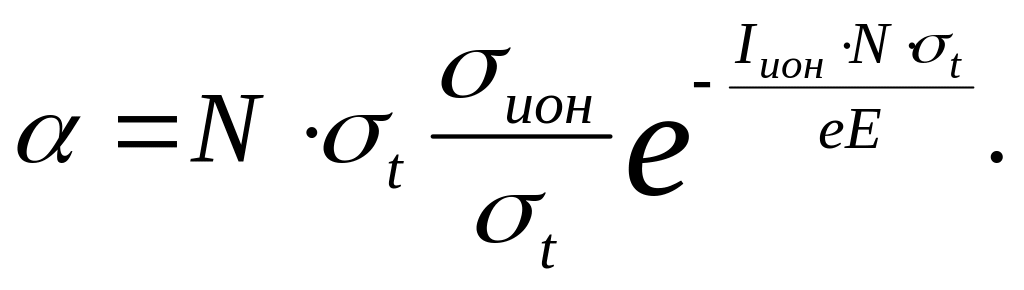
Из приведенного соотношения видно, что число вторичных электронов зависит от пути, пройденного лавиной, от напряженности поля и от свойств газа. Увеличение ионизационного эффекта за счет вторичной ионизации характеризуют коэффициентом газового усиления М, который определяют как отношение числа пар ионов, созданных в счетчике в лавинообразном процессе, к числу пар ионов, созданных ионизирующей частицей. Коэффициент газового усиления можно вычислить, если известна величина . Коэффициент газового усиления резко зависит от того, какой путь прошли электроны. Если бы поле было постоянно, то и = соnst, и тогда величина коэффициента газового усиления была бы резкой функцией места первичной ионизации. Это явление крайне нежелательно, поскольку оно практически исключает возможность определения энергии частицы по созданной ею ионизации. Но вероятность вторичной ионизации сильно зависит от напряженности поля. Поэтому в полях с резким градиентом можно получить очень узкую область, где в основном будет происходить вторичная ионизация. Цилиндрические счетчики, у которых анод выполнен в виде очень тонкой нити с диаметром много меньше диаметра катода, имеют резко неоднородное поле. В таких счетчиках коэффициент газового усиления практически не зависит от места первичной ионизации.

При рассмотрении вторичной ионизации в счетчике предпола­галось, что образующиеся ионы не изменяют поля в счетчике. На самом деле очень большие коэффициенты газового усиления или очень большая первичная ионизация будут приводить к тому, что вокруг анода будет накапливаться большое количество ионов (их скорость дрейфа меньше, чем электронов). Это приведет уменьшению напряженности поля вблизи анода и снижению коэффициента газового усиления.

Процесс вторичной ионизации электронами не единственный в развитии электронной лавины. Дополнительная ионизация может происходить за счет фотонов, испускаемых возбужденными атомами и молекулами. В чистом одноатомном газе фотоионизация может быть только за счет фотоэффекта на катоде счетчика. Но в смеси газов (например, смесь Аг и Хе) возможна фотоионизация атомов одного элемента фотонами, испускаемыми из возбужденных состояний атомов другого элемента, при условии, что энергия фотонов, испускаемых возбужденными состояниями одних атомов, выше энергии ионизации других.

Форма импульса в пропорциональном счетчике

Пусть в цилиндрическом пропорциональном счетчике на расстоянии r_о от его центра в результате первичной ионизации создано п_о пар ионов. Пока в счетчике не наступает газовое усиление, т.е. пока электроны дрейфуют в области низких значений напряженности поля, импульс можно описать соотношением, полученным для цилиндрической камеры. Максимальное значение импульса за счет движения электронов и ионов первичной ионизации будет в М раз меньше, чем результирующий импульс, и, следовательно, этой составляющей импульса можно пренебречь при достаточно больших величинах газового усиления. Лавина электронов начнет развиваться тогда, когда электроны достигнут области r < r_k (k – расстояние от анода, где поле достаточно для вторичной ионизации). Время движения электронов до области газового усиления зависит от места первичной ионизации и составляет примерно (r_о‑r_h)/(w^‑).

Время развития лавины, т.е. время, в течение которого происходит вторичная ионизация, мало. Действительно, газовое усиление осуществляется на расстояниях от центрального электрода, равного нескольким диаметрам нити (~0,1 см). Скорость дрейфа электронов в этой области около 10⁷ см/с, т.е. время развития лавины примерно 10^-8 с. Таким образом, если пренебречь зарядами первичной ионизации, то можно считать, что на расстоянии от центрального электрода около 1…2 диаметров создано M·п_о пар ионов. Оценим отношение максимальных значений амплитуд и . Если r₂/r₁ = 100, a r_к/r₁ ~ 2, то / ≈ 0,15. Таким, образом, мы приходим к интересному выводу: импульс в пропорциональном счетчике обусловлен главным образом движением положительных ионов. Следовательно, в тех случаях, когда производят анализ энергетического состава частиц по амплитудам, необходимо выбирать величины RC больше времени движения положительных ионов от анода к катоду. В силу логарифмической зависимости F(t) в счетчиках можно использовать существенно меньшие величины RC, чем время движения ионов до катода. За время примерно 10^-6 с амплитуда вырастает до половины своего максимального значения. На рис. 2.7 показана форма импульса в пропорциональном счетчике для нескольких значений RC.

Временные характеристики счетчика. Пусть импульс достигает своего максимального значения (или какого-то уровня) за время от момента попадания частицы в счетчик. Длительность этого интервала будет в основном определяться временем движения электронов первичной ионизации от места их образования до анода счетчика и, следовательно, максимальный разброс в величинах будет порядка (r₂ – r_l)/(w ^-).

Флуктуации величины будут зависеть от размеров счетчика, от отношения r₂/r₁ и напряжения на счетчике. Разброс в значениях величин (в зависимости от места первичной ионизации), который может достигать нескольких долей микросекунды и даже микросекунды в больших счетчиках, определяет временное разрешение пропорциональных счетчиков при измерении распределения частиц во времени. Очевидно, что разрешающее время схем совпадений τ_с должно быть больше или порядка неопределенности в .

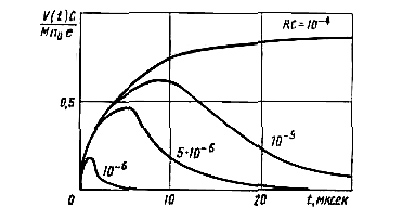
Рис. 2.7. Форма импульса в пропорциональном счетчике.

Время движения ионов от анода к катоду 100 мкс

Если счетчик используется для измерения скорости счета, то представляет интерес время нарастания импульса до определенного значения не от момента попадания частицы в счетчик, а от момента, когда электроны первичной ионизации достигают анода. В этом случае имеет смысл выбирать величины RC малыми, но такими, чтобы амплитуда импульса была еще достаточно большой (чтобы не свести на нет газовое усиление). Когда можно допустить, чтобы амплитуда была в т раз меньше V_max то величины RC можно выбирать из следующего соотношения:

где t_max – время нарастания амплитуды до V_max/m в случае бесконечно большого RC.

Энергетическое разрешение пропорционального счетчика

Величина энергетического разрешения обусловлена флуктуацией в числе пар ионом, созданных ионизирующей частицей. Разброс амплитуд импульсов в пропорциональных счетчиках зависит еще от некоторых причин, влияющих на величину коэффициента газового усиления: объемного заряда, образования электроотрицательных ионов, неравномерности электрического поля вдоль центрального электрода счетчика. Влияние этих причин можно значительно ослабить при разумном выборе параметров и конструкции пропорционального счетчика. Помимо этого, величина коэффициента газового усиления флуктуирует, поскольку процесс газового усиления имеет статистический характер. Величина дисперсии, связанная с процессом первичной ионизации, равна п₀, если считать, что п₀ – случайная величина, распределенная по закону Пуассона.

Уже отмечалось, что полученные формулы для импульсов пропорционального счетчика справедливы, если влияние объемного заряда не существенно и было получено условие, при котором объемный заряд не оказывает заметного влияния на процесс газового усиления:

.

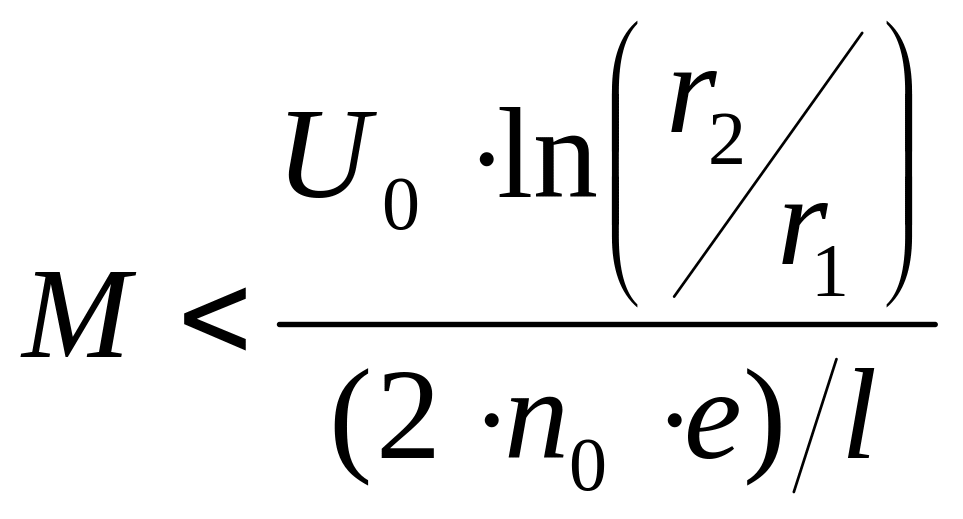Если это условие не выполняется, то коэффициент газового усиления будет падать с ростом энергии частиц и, кроме того, будет различным для частиц с различной ориентацией относительно центрального электрода. Действительно, наибольшая плотность ионов будет тогда, когда частица имеет радиальное направление. В этом случае область, в которой происходит газовое усиление, будет порядка нескольких длин свободного пробега электронов. Наименьшая плотность ионов будет при движении заряженной частицы параллельно оси счетчика. При этом l приблизительно равно длине пробега заряженной частицы в газе счетчика. Работа при больших величинах M возможна при малых давлениях газа в счетчиках. Это можно понять, принимая во внимание, что при уменьшении давления падает пороговое напряжение U_k,. и, кроме того, уменьшается величина п_ое/l при прочих равных условиях. Если влиянием объемного заряда можно пренебречь, то амплитуда импульса пропорционального счетчика практически не будет зависеть от места образования ионов в счетчике при условии, что в счетчике не образуются электро­отрицательные ионы. Для многих газов отношение амплитуды импульсов при ионизации вблизи катода и амплитуды импульсов при ионизации вблизи анода ρ оказалось равным 1. Для газов, в которых вероятность образования электроотрицательных ионов велика, ρ < 1. И это понятно, поскольку коэффициент прилипания является функцией Е/р, и, следовательно, вероятно­сти образования электроотрицательных ионов вблизи анода и вблизи катода могут значительно различаться. Электроотрицательные ионы из-за значительной массы не производят вторичной ионизации. Так, для счетчиков, наполненных BF₃, ρ = 1 при низких давлениях и толстой нити, а при высоких давлениях и тонкой нити ρ << 1. Это объясняют следующими факторами:

1) для BF₃ вероятность прилипания убывает с ростом Е/р, но при заданном Е/р оно пропорционально давлению;

2) напряженность поля вблизи катода тем меньше (при заданном M), чем тоньше нить.

По этим причинам пропорциональные счетчики нейтронов (наполненные BF₃) трудно сделать высокоэффективными за счет увеличения давления газа, необходима тщательная очистка газа от примесей, имеющих большие коэффициенты прилипания.

На энергетическое разрешение счетчиков влияет неравномерность поля, связанная с креплением нити. Для того чтобы избежать искажения поля у концов нити, необходимо крепить нить к охранным электродам специальной формы, тогда неравномерность поля вблизи концов нити можно свести к минимуму. До сих пор неявно предполагалось, что оба электрода счетчика строго коаксиальны. Оказывается, что даже малый эксцентриситет нити приводит к значительным изменениям коэффициента газового усиления.

Можно указать еще одну причину ухудшения энергетического разрешения счетчиков – непостоянство диаметра нити. Неравномерность диаметра нити особенно сказывается на работе счетчиков с очень тонкой нитью.

Флуктуации величины коэффициента газового усиления можно характеризовать величиной среднеквадратичного отклонения:

При больших значениях M среднеквадратичное отклонение такое же, как и для числа пар ионов, образуемых при ионизации. В идеально изготовленном счетчике относительная величина дисперсии при измерениях энергии частиц не может быть меньше, чем

.

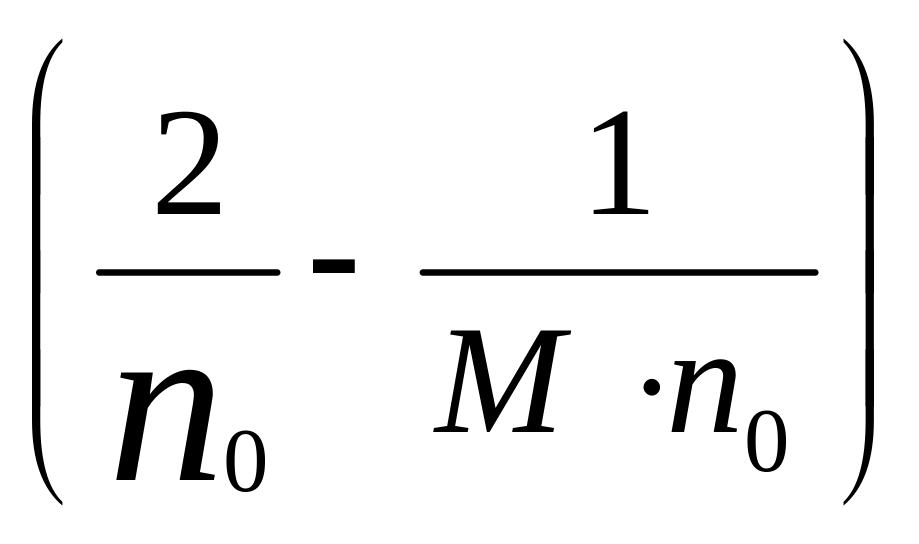В пропорциональных счетчиках при тщательном изготовлении достигают энергетического разрешения порядка 5% при энергиях заряженных частиц около 1 Мэв.