2.3 Расчет регулятора, обеспечивающего заданное качество переходных процессов

Синтезировать непрерывный модальный регулятор по полному вектору состояния, обеспечивающий заданное качество переходных процессов (перерегулирование по выходной переменной σ, время переходного процесса ) с точностью . Численные значения σ и брать из таблицы исходных данных для соответствующей неизменяемой части системы автоматического регулирования. Проверить результаты моделированием на линейной модели.

На рисунке 20 расположены корни исходной системы:

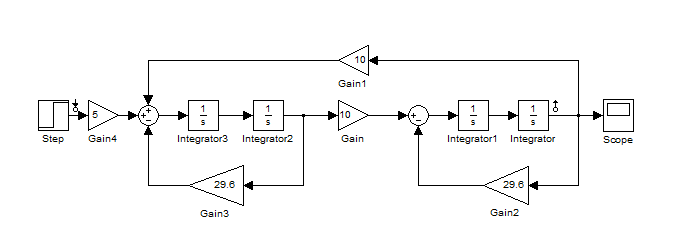
Рис. 19.

Рис. 20.

Для корректировки заданной системы изменим положение четырех корней характеристического уравнения. Рассчитаем положение скорректированных корней. Его действительная часть должна б. Из cотношения , выразим Значит перемещенные корни должны быть

(p_1,2)= .

(p_3,4)= .

Запишем желаемое характеристическое уравнение:

(s+ - j)*(s+ + j)*(s+ - j)*(s+ + j)

Для нахождения коэффициентов регулятора приравняем коэффициенты полиномов при одинаковых степенях. Расчеты коэффициентов выполнены в системе Mathcad и приведены ниже:

Рис. 21.

Из расчета приведенного выше получаем коэффициенты:

K₀₁=-78.7, K₀₂=9.724.58, K₀₃=45.957.6, K₀₄=5.6

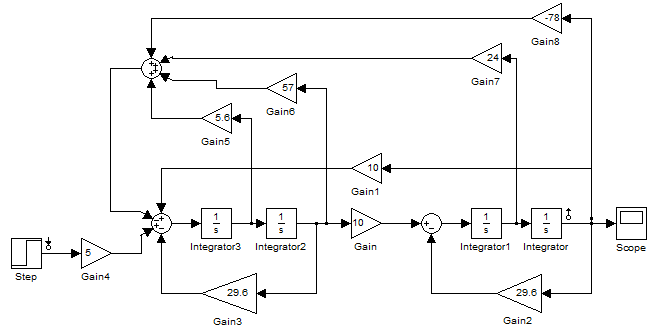
Рис. 22.

Переходная характеристика приведена на рисунке 23:

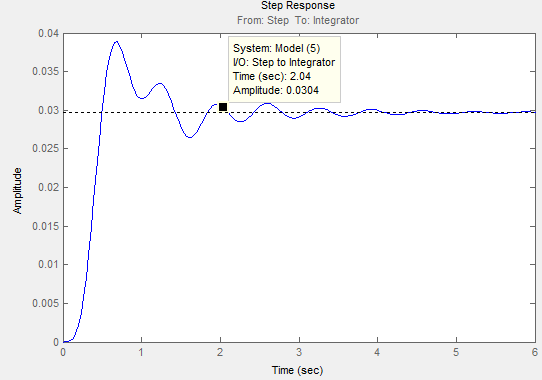
Рис. 23.

Время переходного процесса укладывается в 2 секунды, а перерегулирование в 20%.

2.4 Грубость системы

Изменяя параметры модального регулятора в интервале 10% путем моделирования проверить грубость полученной замкнутой системы.

На рисунке 26 приведена ОСС в Simulink, с увеличенными на 10% коэффициентами (K₀₀₁=32.864, K₀₀₂=8.751, K₀₀₃=7.053, K₀₀₄=3.432):

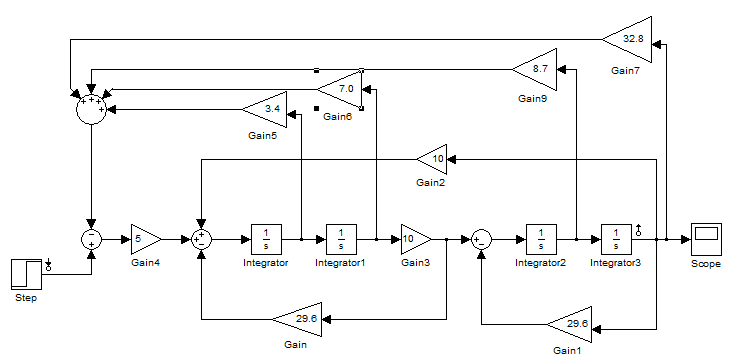
Рис. 24.

На рисунке 27 приведена ОСС в Simulink, с уменьшением на 10% коэффициентами (K₀₁=26.8, K₀₂=7.16, K₀₃=5.7, K₀₄=2.8):

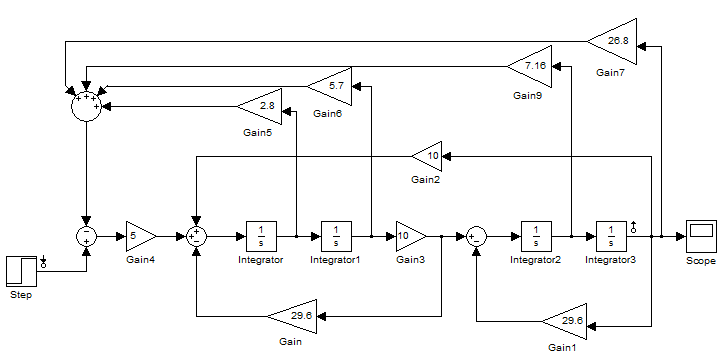
Рис.25.

На рисунке 28 приведены три переходных процесса. Сверху в низ: первый-уменьшение коэффициентов на 10%, второй-с коэффициентами без изменения, третий-с увеличением коэффициентов на 10%. Отсюда видно, что при уменьшении значения коэффициентов на 10%, перерегулирование 22%, а при увеличении значения коэффициентов, перерегулирование 8.4. Следовательно, при изменении модального регулятора в интервале 10%, система не соответствует заданным условиям, значит система грубая.

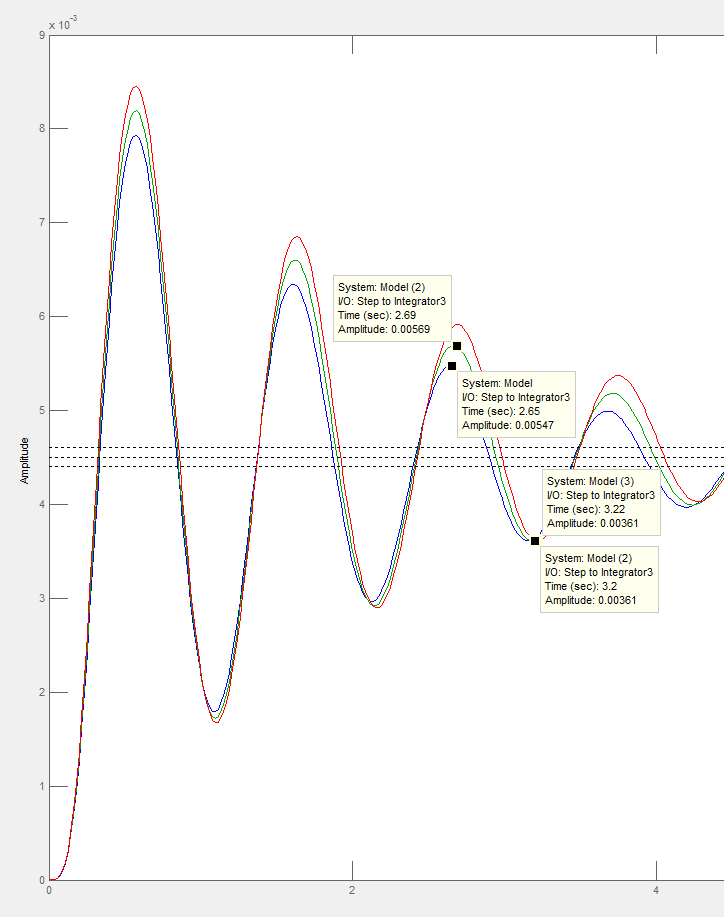
Рис. 26.

2.5 Итерационный синтез пид-регулятора

Провести итерационный синтез ПИД регулятора, ориентируясь на исходные данные пункта 2.4. Начальное приближение получить одним из рекомендованных в данных методических указаниях методов. Проверить результаты моделированием.

Так как уже есть интегратор, следовательно, ошибка исключена, поэтому нам нужно синтезировать ПД регулятор.

Воспользуемся методом Циглера-Никольса. Регулируя пропорциональную составляющую регулятора, добьемся возникновения в системе незатухающих колебаний с периодом Т_кр, и зафиксируем значение К_кр. На рисунке 27 приведена структурная схема в Simulink:

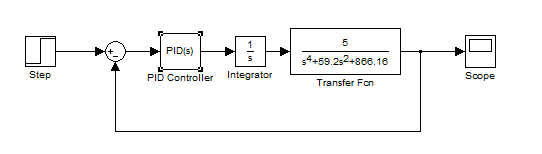
Рис. 27.

График переходного процесса приведен на рисунке 28:

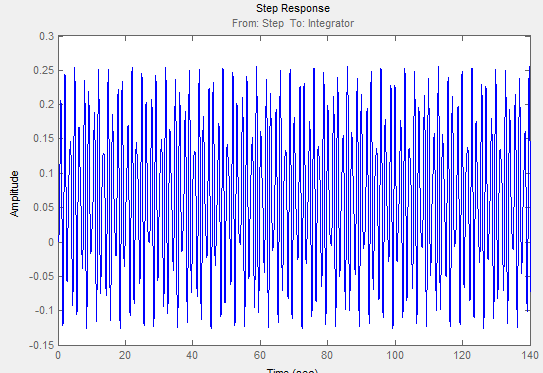
Рис. 28.

Вывели систему на границу устойчивости. Отсюда получаем следующие параметры:

К_кр=51.68 2,7

Т_кр=0,5сек.

Далее рассчитываем и устанавливаем параметры ПД-регулятора:

=0,25 =0,22 =0,24

Смоделируем систему при полученных коэффициентах ПД регулятора (рисунок 29):

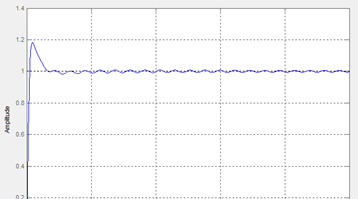
Рис. 29.

Как видно из рисунка, перерегулирование и время переходного процесса устраивают заданным условиям.