2.1 Распределение полюсов по Баттерворту
Синтезировать
непрерывный модальный регулятор по
полному вектору состояния, обеспечивающий
заданное время переходного процесс
с точностью
при распределении полюсов по Баттерворту.
Проверить результаты моделированием
в среде Matlab/Simulink.
Для того чтобы синтезировать модальный регулятор обеспечивающий заданное время переходного процесса, нужно в ОСС из выходов интеграторов провести отрицательную обратную связь с коэффициентами ко входу. Данная ОСС приведена на рисунке11:
Рис. 11.
Распределение Баттерворта для системы 4-го порядка записывается в следующем виде:
Показатели универсальных переходных функций для различных порядков системы, при распределении по Баттерворту представлены в таблице 3.
Таблица 3
n |
1 |
2 |
3 |
4 |
|
3 |
3 |
6 |
7,2 |
σ, % |
– |
4,3 |
8 |
6,2 |
,
о.е.
Отсюда желаемое характеристическое уравнение имеет вид:
Найдем характеристическое уравнение ОСС матричного характеристического уравнения:
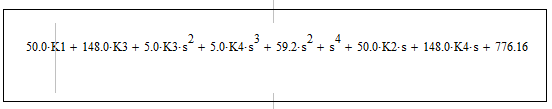
Рис. 12.
Преобразуем данное выражение к следующему виду:
Для нахождения коэффициентов регулятора приравняем коэффициенты полиномов при одинаковых степенях. Расчеты коэффициентов выполнены в системе Mathcad и приведены ниже:
Рис.
13.
Из расчета приведенного выше получаем коэффициенты:
K01=3.20
K02=5.19
K03=3.03
K04=1.87
Проверку выполним в Simulink. На рисунке 15 приведена ОСС выполненная в Simulink с учетом коэффициентов рассчитанных по Баттерворту:
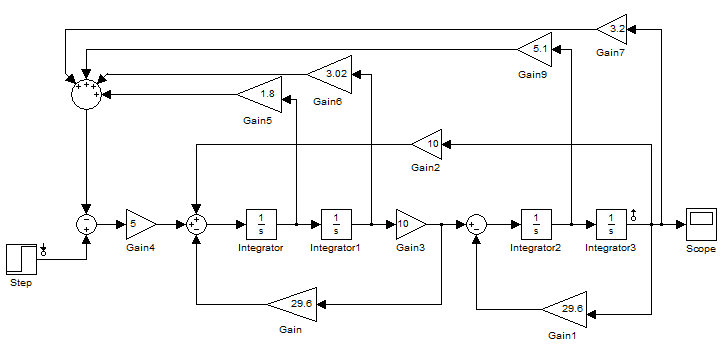
Рис. 14.
Переходная характеристика с коэффициентами по Баттерворту приведена на рисунке 15:
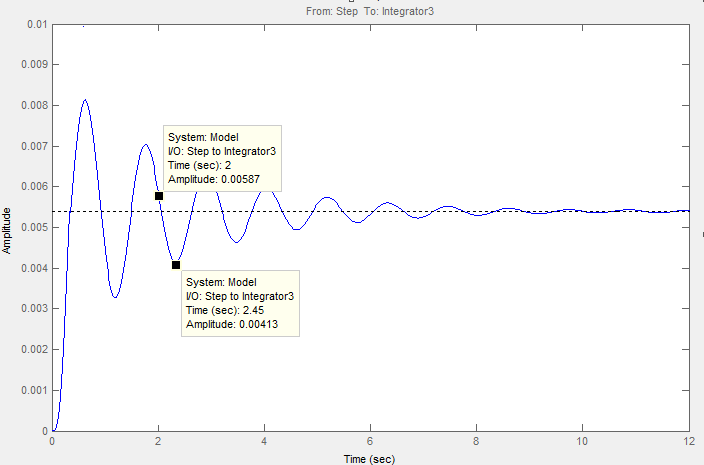
Рис. 15.
Из рисунка 15 видно, что время переходного процесса за 2 с, обеспечивает перерегулирование 20% .
2.2 Биноминальное распределение
Синтезировать непрерывный модальный регулятор по полному вектору состояния, обеспечивающий заданное время переходного процесс с точностью при биномиальном распределении полюсов. Проверить результаты моделированием.
Желаемое характеристическое уравнение найдем из Бинома Ньютона для 4-го порядка который имеет вид:
Для каждого порядка системы будет свое относительное время переходного процесса . Для систем до 4-го порядка включительно оно указано в табл. 4.
Таблица 4
|
1 |
2 |
3 |
4 |
в относительных единицах (о.е.) |
3 |
4,75 |
6,3 |
7,8 |
Желаемое характеристическое уравнение примет вид:
Для нахождения коэффициентов регулятора приравняем коэффициенты полиномов при одинаковых степенях. Расчеты коэффициентов выполнены в системе Mathcad и приведены ниже:
Рис. 16.
Из расчета приведенного выше получаем коэффициенты:
K001=29.8, K002=7.95, K003=6.412, K004=3.12
Проверку выполним в Simulink. На рисунке 17 приведена ОСС выполненная в Simulink с учетом найденных коэффициентов:
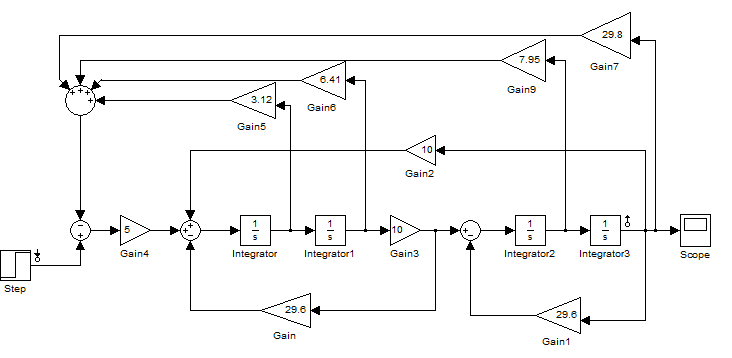
Рис. 17.
Переходная характеристика приведена на рисунке 18.
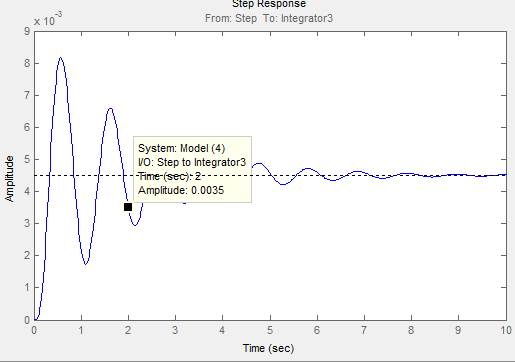
Рис. 18
Получили время переходного процесса 2 секунд, что полностью удовлетворяет заданному качеству переходного процесса. Перерегулирование 20%.