24. Теорема о циркуляции вектора в в интегральной и дифференциальной формах.

Ц иркуляция вектора B(с вектором) по произвольному контуру Г равна произведению на алгебраическую сумму токов, охватываемых контуром Г:

- алгебраическая сумма токов. Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта.

В дифференциальной форме:

Правило токов:

24. Магнитное поле движущегося заряда.

Э лектрический ток – это движение зарядов. Следовательно, движущиеся заряды создают вокруг себя магнитное поле:

С илу тока выразим через плотность:

Учтем, что

N- кол-во молекул; n- концетрация в единице объема; е – заряд.

Находим: - индукция поля положительного заряда, движущегося со скоростью u.

24. С ила Лоренца.

Сила, действующая на проводник с током:

Подставим:

Сила, действующая на одну частицу, - магнитная составляющая силы Лоренца.

~ Модуль силы равен: где - угол между вектором В и вектором u.

~ Направление силы определяется правилом левой руки/

~ В электромагнитном поле на частицу действует полная сила Лоренца, равная:

30. Движение заряженной частицы в магнитном поле

1.  Заряженная частица влетает в магнитное поле со скоростью , направленной вдоль поля  или противоположно  направлению магнитной индукции поля   .

В этих случаях сила Лоренца      и частица будет продолжать двигаться равномерно прямолинейно.

2. Заряженная частица движется перпендикулярно линиям магнитной индукции

тогда сила Лоренца   , следовательно, и сообщаемое ускорение будут постоянны по модулю и перпендикулярны к скорости частицы.

В результате частица будет двигаться по окружности , радиус которой можно найти на основании второго закона Ньютона:    

О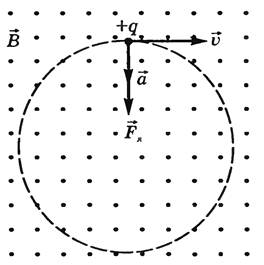 тношение       — называют удельным зарядом частицы.  

Период вращения частицы

то есть период вращения не зависит от скорости частицы и радиуса траектории.

3. Скорость заряженной частицы направлена под углом  к вектору.

   Движение частицы можно представить в виде суперпозиции равномерного прямолинейного движения вдоль поля со скоростью  и движения по окружности с постоянной по модулю скоростью  в плоскости, перпендикулярной полю.

Радиус окружности определяется аналогично предыдущему случаю, только надо   заменить  на   , то есть

В результате сложения этих движений возникает движение по винтовой линии, ось которой параллельна магнитному полю. Шаг винтовой линии

Направление, в котором закручивается спираль, зависит от знака заряда частицы.

Если скорость заряженной частицы составляет угол α с направлением вектора     неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, тο R и h уменьшаются с ростом B. На этом основана фокусировка заряженных частиц в магнитном поле.

Если на движущуюся заряженную частицу помимо магнитного поля с индукцией  действует одновременно и электростатическое поле с напряженностью , то равнодействующая сила, приложенная к частице, равна векторной сумме электрической силы и силы Лоренца:   . Характер движения и вид траектории зависят в данном случае от соотношения этих сил и от направления электростатического и магнитного полей.