15.Электроемкость сферического конденсатора

Н айдем разность потенциалов между обкладками конденсатора, воспользуемся связью между напряженностью и потенциалом

Напряженность поля

М ежду обкладками может находиться диэлектрик

16. Электроемкость цилиндрического конденсатора

Расчет емкости проведем тем же способом, что и в случае сферического конденсатора

Е сли учесть наличие диэлектрика

Е сли d<<a,b то

17. Энергия взаимодействия зарядов

Р ассмотрим энергию взаимодействия двух зарядов, которые в результате кулоновского взаимодействия совершили перемещения на

П ри этом силами поля совершена работа

Работа равна убыли потенциальной энергии

О бобщая на систему зарядов можно записать для системы точечных зарядов

где - потенциал, создаваемый всеми остальными зарядами системы в месте нахождения заряда. Если заряды распределены непрерывно, то

- потенциал, создаваемый всеми зарядами системы в элементе объема

17. Энергия электрического поля (уединенный проводник, конденсатор).

Энергию системы зарядов можно выразить не только через заряд и потенциал, но и через характеристику поля – напряженность.

В случае плоского конденсатора

В общем случае для изотропной среды

Первое слагаемое – энергия поля в вакууме,

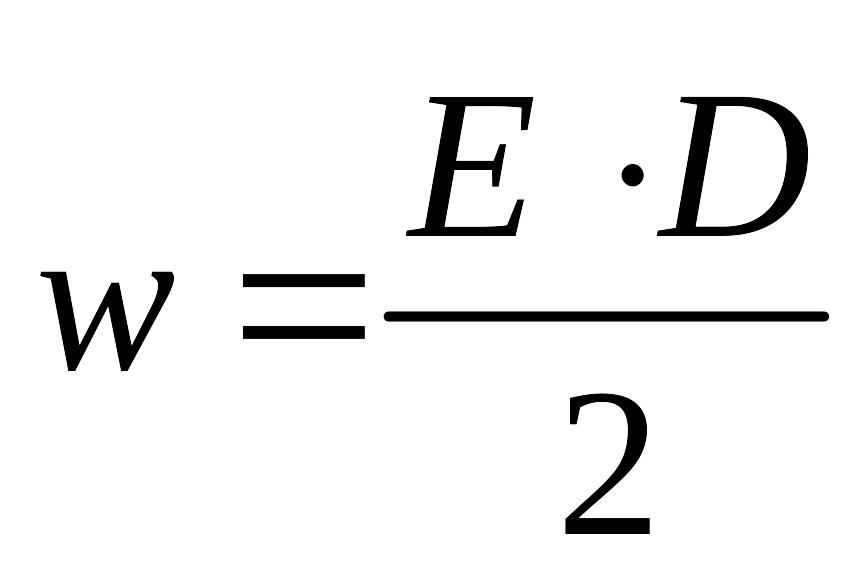второе слагаемое – энергия, связанная с поляризацией диэлектрика

Э нергия поля распределяется в пространстве с объемной плотностью

Д ля уединенного проводника

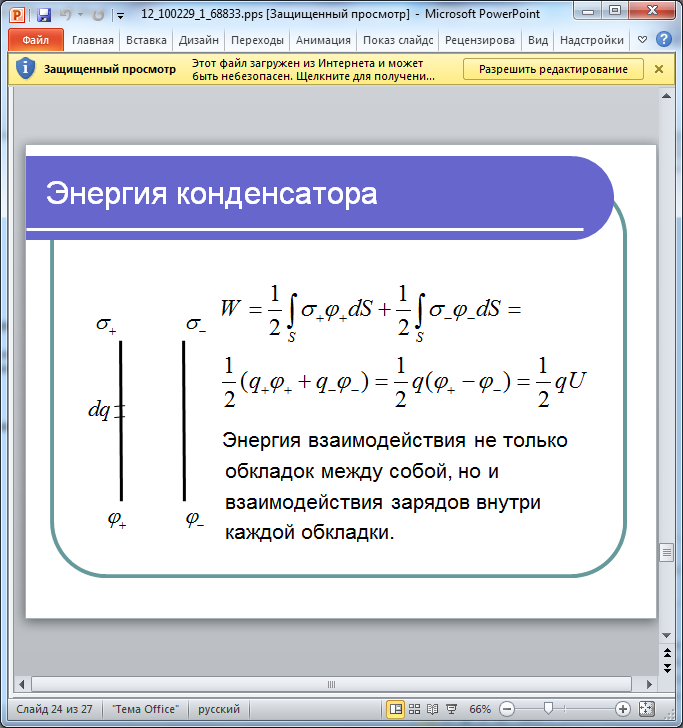
Энергия конденсатора

19.Характеристики и условия существования электрического тока.

Электрический ток – это упорядоченное движение носителей заряда.

Для существования электрического тока необходимо: 1) наличие зарядов, способных перемещаться в пределах тела;

2) в проводнике должно существовать электрическое поле.

К оличественной мерой тока служит сила тока - заряд, перенесенный через заданную поверхность S (или через поперечное сечение проводника), в единицу времени, т.е.:

За направление тока принято направление движения положительных зарядов.

Характеристики:

• Э лектрический ток может быть распределен по сечению проводника неравномерно. Поэтому для детальной характеристики тока вводят вектор плотности тока

• М одуль плотности тока численно равен заряду, переносимому через единичную площадку, расположенную в данной точке перпендикулярно направлению движения носителей, за единицу времени

Е сли обозначить через скорость упорядоченного движения зарядов, то

- объемные плотности положительного и отрицательного зарядов.

Плотность тока и сила тока связаны соотношением

Поле вектора можно изобразить графически с помощью линий тока, которые проводятся так же как и линии напряженности

Условия существования:

• Электрический ток – это упорядоченное движение носителей заряда.

• Для существования электрического тока необходимо: 1)наличие зарядов, способных перемещаться в пределах тела; 2) в проводнике должно существовать электрическое поле.

2 0. Уравнение непрерывности. 

П редставим себе в некоторой проводящей среде, где течет ток, замкнутую поверхность Для замкнутых поверхностей положительной нормалью считается внешняя нормаль, поэтому дает заряд,

выходящий за единицу времени наружу из объема , охваченного поверхностью

И з закона сохранения заряда следует, что этот интеграл равен убыли заряда в единицу времени внутри объема. Т.е.

Данное равенство называется уравнением непрерывности.

В случае стационарного тока так как

Преобразуем уравнение

Введем среднюю плотность заряда, тогда

Стянув поверхность в точку, получим

- уравнение непрерывности в дифференциальной форме.

Для постоянного тока (Уравнение означает, что в случае постоянного тока поле вектора не имеет источников (линии замкнуты).