
- •Свойства заряда. Закон Кулона. Электрическое поле и его силовая характеристика.
- •Напряженность поля точечного заряда. Принцип суперпозиции электрических полей
- •Теорема Гаусса для вектора е в интегральной и дифференциальной формах.
- •Энергетическая хар-ка поля -потенциал. Потенциал точечного заряда. Принцип суперпозиции потенциалов.
- •Теорема о циркуляции вектора e
- •Связь между напряженностью поля и разностью потенциалов
- •Силовые линии и эквипотенциальные поверхности. Свойства силовых линий.
- •Типы диэлектриков. Поляризованность.
- •Теорема Гаусса для вектора р.
- •Поведение вектора р на границе раздела двух сред.
- •Вектор электрического смещения d. Теорема Гаусса для вектора d.
- •Поле внутри проводника. Статический случай.
- •14. Электроемкость уединенного проводника и конденсатора. Плоский конденсатор.
- •15.Электроемкость сферического конденсатора
- •16. Электроемкость цилиндрического конденсатора
- •Энергия взаимодействия зарядов
- •Энергия электрического поля (уединенный проводник, конденсатор).
- •19.Характеристики и условия существования электрического тока.
- •21. Закон Ома и закон Джоуля-Ленца в дифференциальной форме.
- •22. Классическая теория электропроводности (Теория Друде)
- •23.Магнитное поле и его силовая характеристика. Сила Ампера. Закон Био-Савара-Лапласа.
- •Принцип суперпозиции магнитных полей. Магнитное поле кругового тока.
- •Виток с током в магнитном поле.
- •Линии вектора магнитной индукции. Теорема Гаусса для вектора в.
- •Теорема о циркуляции вектора в в интегральной и дифференциальной формах.
- •Магнитное поле движущегося заряда.
- •С ила Лоренца.
- •30. Движение заряженной частицы в магнитном поле
- •31. Эффект Холла
- •32.Явление электромагнитной индукции. Контур движется в магнитном поле.
- •33.Явление электромагнитной индукции. Контур неподвижен.
- •34. Явление самоиндукции. Ток размыкания.
- •35. Явление самоиндукции. Так замыкания.
- •36. Взаимная индукция.
- •37. Магнитная энергия поля.
- •38. Магнитная энергия двух контуров с токами.
- •39. Магнитное поле в веществе. Намагниченность. Токи намагничивания.
- •40.Напряжённость магнитного поля. Теорема о циркуляции вектора н.
- •41. Условия на границе раздела двух магнетиков.
- •42. Ток смещения
- •43.Уравнения Максвелла и их свойства.
- •44. Уравнения Максвелла для стационарных полей и нейтральных непроводящих сред.
- •45. Электромагнитные волны.
- •46. Плоская электромагнитная волна. Вектор Умова-Пойтинга.
- •47. Излучение диполя.
- •48. Интерференция света (два когерентных источника).
- •49. Интерференция в тонких пленках.
- •50. Многолучевая интерференция.
- •51. Дифракция света на круглом отверстии.
- •52. Дифракция света на круглом диске.
- •53. Дифракционная решетка.
51. Дифракция света на круглом отверстии.
Дифракцией называется совокупность явлений, проявляющихся в перераспределении светового потока в результате суперпозиции волн, наблюдаемых при распространении света в среде с резкими неоднородностями.
П оместим
между источником света и экраном
наблюдения экран с отверстием. Наблюдение
будем вести в точке Р, кот лежит на
прямой, проходящей через источник света
и центр первой зоны Френеля. Результат
наблюдения в точке Р будет зависеть от
того, какое кол-во зон Френеля уместится
в круглое отверстие.
оместим
между источником света и экраном
наблюдения экран с отверстием. Наблюдение
будем вести в точке Р, кот лежит на
прямой, проходящей через источник света
и центр первой зоны Френеля. Результат
наблюдения в точке Р будет зависеть от
того, какое кол-во зон Френеля уместится
в круглое отверстие.
Если в отверстие укладывается нечетное число зон Френеля, то в точке наблюдения Р будет максимум эффективности, т.е. светлое пятно. Если же четное число зон Френеля, то темное пятно.
Для
расчета интенсивности в точке Р
воспользуемся следующим представлением:
![]()
![]()
![]()
![]()
![]()
![]()
По мере перемещения точки наблюдения вдоль экрана число открытых зон меняется и в точке наблюдения максимум будет сменяться на минимум интенсивности и так далее. Если кол-во открытых (частично) четных зон превышает кол-во открытых (частично) нечетных зон, то в точке наблюдения будет темное пятно, в противном случае светлое.
52. Дифракция света на круглом диске.
М ежду
источником света и точкой наблюдения
Р пометим непрозрачный круглый диск
радиуса r.
ежду
источником света и точкой наблюдения
Р пометим непрозрачный круглый диск
радиуса r.
Диск закроет m первых зон Френеля, амплитуда в точке Р будет

Характер картины на экране можно выяснить с помощью тех же самых рассуждений, как и в дифракции на круглом отверстии.
53. Дифракционная решетка.
Дифракционная решетка – совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние щелей. Расстояние между соседними щелями называется периодом решетки.
Дифракционная картина от дифракционной решетки явл-ся совокупностью двух картин: дифракция от одной щели и многолучевой интерференции, при условии, что пространственная когерентность выполняется для всей дифракционной решетки. В этом случае волны, идущие от разных щелей явл-ся когерентными.
П ри
рассмотрении многолучевой интерференции
нами была получена формула
ри
рассмотрении многолучевой интерференции
нами была получена формула
![]()
Из
рисунка ясно, что
![]()
Тогда
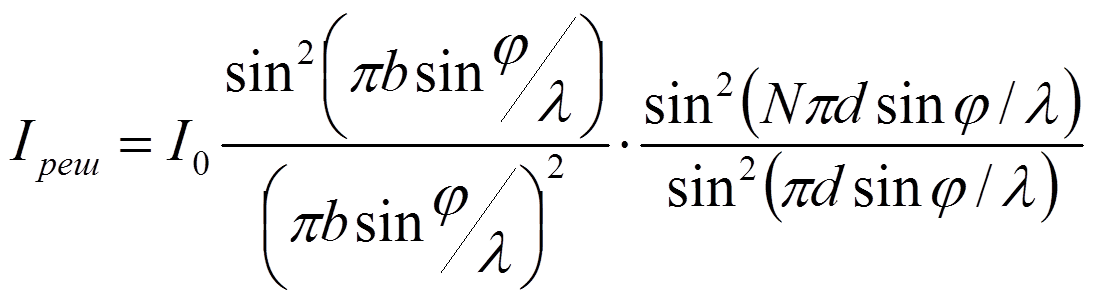
Первый
множитель обращается в нуль, если
![]() (1)
(1)
![]()
![]()
В этих точках интенсивность, создаваемая каждой из щелей в отдельности, равна нулю.
Второй
множитель принимает значение N2
в точках
![]() (2)
(2)
![]()
Для направлений, определяемых этим условием, колебания от щелей друг друга усиливают.
Условие (2) определяет положение главных максимумов.
З апишем
еще одно условие, определяющее положение
N-1
минимума, которое получили названия
добавочных минимумов:
апишем
еще одно условие, определяющее положение
N-1
минимума, которое получили названия
добавочных минимумов:
![]() (3)
(3)
![]() =1,2,…N-1,
N+1,…
2N-1,
2N+1,…
=1,2,…N-1,
N+1,…
2N-1,
2N+1,…
При = , 2 … условием минимума переходит в условие максимума.
Условия, определяющие дифракционную картину от дифракционной решетки:
![]()
![]()
![]()
![]()
![]() =1,2,…N-1,
N+1,…
2N-1,
2N+1,…
=1,2,…N-1,
N+1,…
2N-1,
2N+1,…
