49. Интерференция в тонких пленках.

Плоскопараллельная пластина:

П усть на плоскопараллельную пластину падает параллельный пучок света. Пластина отбросит два пучка света – один, отраженный от верхней поверхности, второй – от нижней.

Дополнительная разность хода появляется в случае отражения луча от границы с оптически более плотной средой. При отражении от оптически более плотной реды фаза волны изменяется на pi, что и соответствует изменению разности хода на

Далее

Окончательно

Все лучи, падающие на пластину под углом , при выполнении условия , дадут максимум интенсивности в интерференционной картине.

Интерференц.картина на плоскопараллельной пластине получиланазвание полос равного наклона. Эта картина набл-ся в параллельных лучах, локализована на бесконечности, реально набл-ся в факальной плоскости собирающей линзы, представляет собой чередующиеся темные и светлые кольца.

Другая интерференц.картина набл-ся на клинообразных пленках и имеет название полосы равной толщины.

При условии выполнения пространственной и временной когерентности полосы равной толщины не локализованы, наблюдаются на любом удалении от пленки и представляют собой чередующиеся темные и светлые полосы, параллельные грани при вершине клина.

При ограниченной и пространственной когерентности полосы равной толщины набл-ся только вблизи поверхности клина.

При малых углах при вершине клина для оценки разности хода лучей можно использовать ту же формулу, что и для полоски параллельной пластины.

В условии интерференции максимума будет выполнятся для всех точек поверхности клина, для кот толщина клина одинакова.

Кольца Ньютона

Одним из примеров полос равн.толщины явл-ся кольца Ньютона. Они образуются при отражении светового пучка от тонкой пленки переменной толщины, роль кот.играет «воздушный клин», который образуется между плоскопараллельной пластиной или линзой большого радиуса кривизны.

Н айдем радиусы колец Ньютона

Так как , то . Если , то .

появляется при отражении от нижней границы воздушного клина.

Определим толщину клина в месте наблюдения кольца радиусом r.

В силу малости толщины клина

Таким образом, в точках, удовлетворяющих условию будут наблюдаться интерференционные max, а в точках, удовлетворяющих условию , будут наблюдаться интерференционные min.

Объединив эти условия, получим

Четным m соответствуют радиусы светлых колец, нечетным – темных. При m=1, r=0 наблюдается темное пятно в месте касания линзы и пластинки (результат изменения фазы на ).

50. Многолучевая интерференция.

Рассмотрим результат наложения N-го кол-ва когерентных волн, для упрощения расчета предположим, что в точке наблюдения волны возбуждают колебания одинаковой амплитуды, а фаза складывающихся колебаний изменяется регулярным образом на величину .

Запишем выражения для этих колебаний:

N – число источников света.

Сложим эти колебания с помощью фазовой диаграммы, представив колебание вектором и углом поворота относительно выбранной оси, равным начальной фазе.

Перенесем вектора способом, показанным на рис. т.к. длины векторов равны и они поворачиваются друг относительно друга на один и тот же угол, то их совокупность образует часть правильного многоугольника, вокруг которого может быть описана окружность некоторого радиуса R.

О чевидно, что

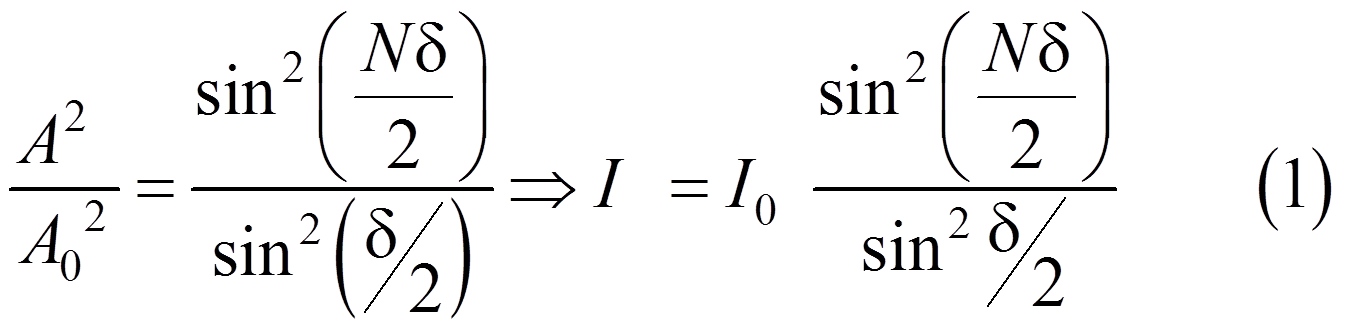
При , что соответствует разности хода выражение (1) становится неопределенным. Раскроем неопределенность следующим способом. При

Интенсивность волн, создаваемых источниками, оказывается в N² раз больше интенсивности, создаваемой отдельным источником. Точки, для которых , а называются главными максимумами.

Анализ функции показывает, что между двумя соседними главными максимумами располагаются N-2 вторичных максимума, интенсивность которых значительно слабее.

Вторичные максимумы интерференции наблюдаются, когда числитель выражения (1) обращается в ноль. Это происходит, когда (не кратно N!)