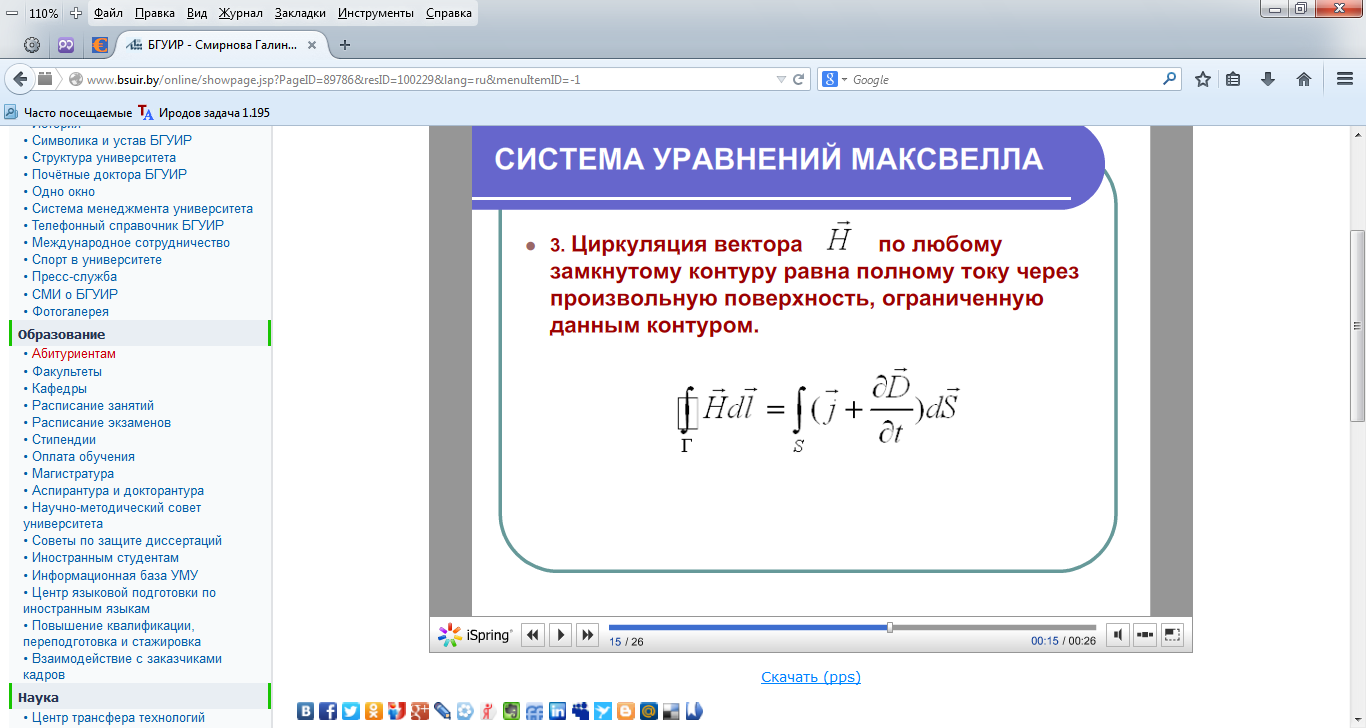
43.Уравнения Максвелла и их свойства.
Г
оворят,
что
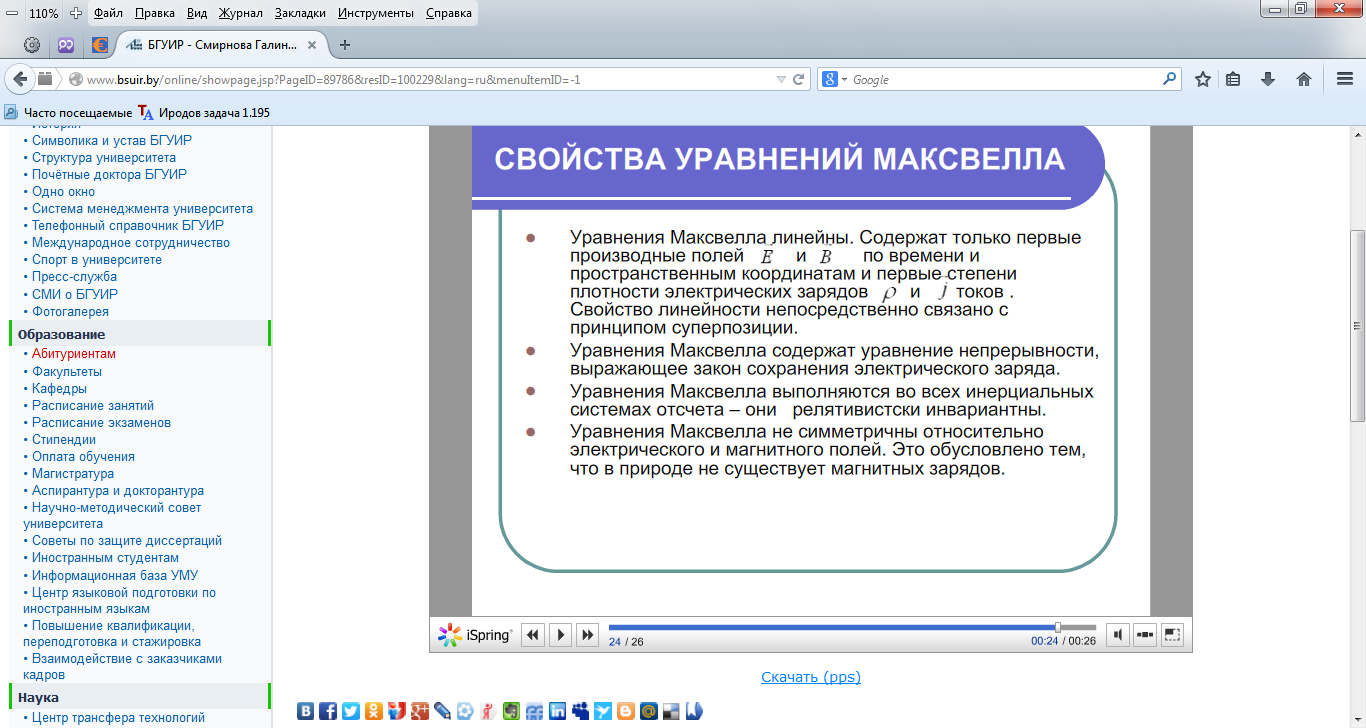
Свойства уравнений:
44. Уравнения Максвелла для стационарных полей и нейтральных непроводящих сред.
Стационарные поля – поля постоянные во времени
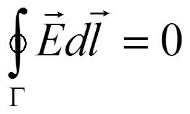
В нейтральной непроводящей среде, где
,
, уравнения Максвелла приобретают
симметричный
вид с точностью до знака:
45. Электромагнитные волны.
Рассмотрим
однородную нейтральную
непроводящую среду
с постоянными
и
.
Запишем уравнения Максвелла и дополним
их материальными условиями
Произведем подстановку материальных условий в уравнения
Возьмем
ротор от обеих частей уравнений
Раскроем
ротор ротора
и
используем
Получим:
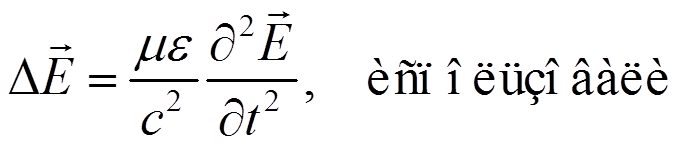
(1)
Аналогичная процедура для второго уравнения приводит к результату:
(2)
. Учтем, что
(3). Уравнения (1) и (2) представляют собой
типичные волновые уравнения. Функция,
удовлетворяющая такому уравнению,
описывает волну, распространяющую с
фазовой скоростью (3).
Электромагнитная волна – процесс распространения электромагнитного поля в пространстве.
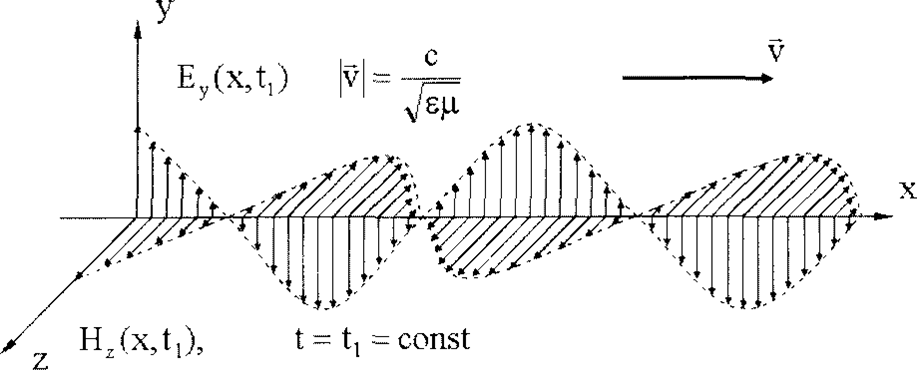
46. Плоская электромагнитная волна. Вектор Умова-Пойтинга.
Волновое уравнение плоской электромагнитной волны, распространяющейся вдоль оси х имеет вид:
Простейшим решением этих уравнений являются функции
Уравнение электромагнитной волны в векторной форме:
,
причем
Свойства электромагнитных волн:
скорость распространения волн в непроводящей нейтральной неферромагнитной среде
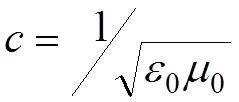
векторы
- взаимно перпендикулярны и образуют
правовинтовую систему;
в электромагнитной волне векторы
и
всегда колеблются в одинаковых фазах,
причем между мгновенными значениями
и
в любой точке существует связь
Вектор Умова-Пойтинга:
Электромагнитные волны переносят энергию. Плотность потока энергии можно получить, если умножить плотность энергии на скорость распространения волны. Плотность энергии электромагнитной волны:
.
Т.к.
,
то
,
что можно записать в виде:
Умножив
,
получим для плотности потока энергии
Т.к.
и
образуют правовинтовую систему, то
вектор
совпадает с направлением распространения
волны и равен по модулю
.
Следовательно,
вектор плотности потока энергии
Вектор
называется вектором
Пойтинга.
Поток
электромагнитной энергии через
произвольную поверхность
можно найти как
Вектор Умова-Пойтинга показывает не только какая энергия переносится в данном направлении, но и направление переноса энергии.
47. Излучение диполя.
Простейшей
системой, излучающей электромагнитные
волны, является колеблющийся
электромагнитный диполь. Примером
такого диполя может служить система из
неподвижного заряда
и колеблющегося около него точечного
заряда
,
либо неподвижный диполь, заряд которого
изменяется по гармоническому закону.
Дипольный электрический момент такой
системы изменяется со временем по закону
-
радиус – вектор заряда
,
-
амплитуда колебаний,
-
единичный вектор, направленный вдоль
оси диполя
Р
ассмотрим
излучение диполя, размеры которого малы
по сравнению с
.
Такой диполь называется точечным.
В непосредственной близости от диполя
картина электромагнитного поля очень
сложная. Она сильно упрощается в так
называемой волновой зоне диполя, которая
начинается на расстояниях
.
Точечный
диполь дает сферическую волну в однородной
изотропной среде. Вектор
излучение диполя всегда направлен по
касательной медиане, а вектор
- по касательной к параллели и оба они
к лучу
,
который задает направление распространения
электромагн.волны. К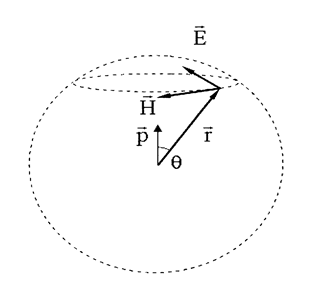
олебание
вектора
и
происходит в одинаковой фазе по закону
.
Амплитуды векторы
и
зависят от расстояния между точкой
наблюдения и диполем, а также от угла
под которым рассматривается излучение.
Для вакуума эта зависимость имеет вид
.
Среднее
значение потока энергии пропорционально
,
следовательно
Из этой формулы вытекает, что интенсивность убывает с ростом расстояния от диполя, кроме того интенсивность оказывается зависящей от угла , под которым рассматривается излучение. Наиболее интенсивно излучает в направления, перпендикулярных его оси и не излучает в направлении совпадающим с осью диполя.