3.2. Примеры решения задач
Пример 1.
Сосуд с прямоугольным основанием
наполнен
водой до высоты h
и движется по горизонтальной поверхности
с ускорением a
(рис. 3.3). Определить избыточное давление
воды на дно сосуда у передней и задней
стенок в точках 1 и 2.
Решение:
При горизонтальном движении сосуда с
ускорением a
свободная поверхность жидкости станет
наклонной к горизонту под углом
. Так как
,
то
.
Учитывая что объем воды не изменяется,
поэтому свободная поверхность повернется
вокруг оси О, расположенной на середине
длины сосуда, а повышение и понижение
свободной поверхности у торцовых стенок
будет одинаковым и равным
.
.
Избыточное давление в точке 1 будет равно:
.
В точке 2 избыточное давление составит:
.
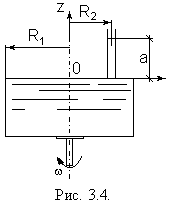
Пример 2. Цилиндрический сосуд радиусом R1 наполнен жидкостью плотностью до уровня a в открытой трубке малого диаметра, установленной на крышке сосуда на расстоянии R2 от центра, и приведен в равномерное вращение относительно центральной вертикальной оси (рис. 3.4). Определить угловую скорость вращения сосуда, при которой избыточное давление под крышкой в центре сосуда будет равно 0.
Решение:
Используя уравнение (3.15) найдем закон
распределения избыточного давления в
жидкости, заполняющей сосуд, учитывая
что
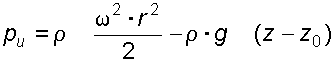
находим,
используя граничное условие:
при
и
откуда
.
Подставляя, получим искомый закон распределения давления.
.
Для точек на
поверхности крышки
имеем
.
Искомую угловую
скорость вращения определяем из условия
при
,
откуда
.
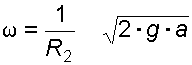3.3 Задания для расчетно-графических работ
Вариант 1
Задача 1
Определить коэффициент динамической и кинематической вязкости воды, если шарик d = 2 мм из эбонита с = 1,2 103 кг/м3 падает в воде с постоянной скоростью u = 0,33 м/с. Плотность воды = 103 кг/м3.
Задача 2
Рис.1
Определить абсолютное и избыточное гидростатическое давление в точке А (рис. 1), расположенной в воде на глубине hA = 2,5M, и пьезометрическую высоту для точки А, если абсолютное гидростатическое давление на поверхности p0 = 147,2кПа.
Задача 3
Медный шар d = 100 мм весит в воздухе 45,7 H, а при погружении в жидкость 40,6 H. Определить плотность жидкости.
Задача 4
Определить на сколько процентов увеличится начальный объем воды, спирта и нефти при увеличении температуры на 10°С?
Задача 5
На зафиксированный на полу поршень, опирается цилиндрический сосуд без днища, заполненный водой. Определите величины давления p1 и p2, если вес сосуда G= 103 Н; ρв = 1 т \ м3, высота столба жидкости h = 0,8M; диаметр сосуда D = 0,4 М.
Вариант 2
Задача 1
При гидравлическом испытании системы объединенного внутреннего противопожарного водоснабжения допускается падение давления в течение 10 мин. на p = 4,97104 Па. Определить допустимую утечку W при испытании системы вместимостью W = 80 м3. Коэффициент объемного сжатия w= 5 10-10 Па-1.
Задача 2
Рис.3.
Определить давление в резервуаре p0 (рис. 3) и высоту подъема уровня h1 в трубке 1, если показания ртутного манометра h2 =0,15M, h2 =0,8M,
ρрт = 13, 6 т \ м3 ρв = 1 т \ м3.
Задача 3
рис.4
Идеальная жидкость относительной плотностью δ= 0,8 перетекает через систему трех трубопроводов с диаметрами d1=50мм, d2=70мм, d3= 40мм под постоянным напором Н = 16м. трубопроводы полностью заполнены жидкостью. Определить расход жидкости Q.
Задача 4
Рис. 5
Определить все виды гидростатического давления в баке с нефтью на глубине Н = 3м (рис.5 ), если давление на свободной поверхности нефти 200 кПа. Плотность нефти ρ = 0,9 т\м3 .
Задача 5
Определить критическую скорость, отвечающую переходу от ламинарного режима к турбулентному в трубе диаметром d = 0,03мм при движении воды, и глицерина при температуре 25 °С.
Вариант 3
Задача 1
Определить изменение плотности воды при нагревании ее от t1=7 °С до t2=97 °С.
Задача 2
Рис.6.
Определить манометрическое давление в трубопроводе А (рис. 6), если высота столба ртути по пьезометру h2=25 см. Центр трубопровода расположен на h1=40 см ниже линии раздела между водой и ртутью.
Задача 3
Расход идеальной жидкости относительной плотности δ = 0,86 в расширяющемся трубопроводе с диаметрами d1= 480мм в сечении 1 – 1и d2 = 945мм в сечении 2 – 2, равен = 0,18м3\с (рис. 7). Разница в позициях сечений равна 2 м. Показатель манометра в сечении 1 – 1 равно p1 = 3 *105 н\м2. Определить скорость воды в сечениях 1 – 1и 2 – 2; давление p2 в сечении 2 – 2.
Рис.7
Задача 4
Определить число Рейнольдса и режим движения воды в водопроводной трубе диаметром d = 300мм при расходе Q = 0,136 м3\с и температуре воды 10 °С.
Задача 5
Рис.8
Резервуары А и В с водой соединены горизонтальным трубопроводом состоящим из отрезков труб с диаметрами d1 = 100 мм и d2 = 60 мм и имеющими кран с коэффициентом местных потерь ζ= 5 (рис. 8). Другими потерями можно пренебречь. Разница в уровнях жидкости в резервуарах Н = З м. Определить расход жидкости в трубопровода Q. Каким должен быть коэффициент местных потерь ζ, чтобы расход жидкости Q увеличился в два раза?
Вариант 4
Задача 1
Определить давление внутри капли воды диаметром d = 0,001м, которое создают силы поверхностного натяжения. Температура воды t1=20 °С
Задача 2
Определить избыточное давление воды в трубе по показаниям батарейного ртутного манометра (рис. 9).
Рис.9
Отметки уровней ртути от оси трубы: z1 = 1,75 М; z2 = 3 М; z3 = 1,5 М;
z4 = 2,5 М; Плотность ртути ρрт = 13, 6 т \ м3, плотность воды ρв = 1 т \ м3.
Задача 3
Рис.10
Наклонный трубопровод состоит из четырех составных частей с диаметрами d1 = 100 мм, d2 =75мм, d3 = 50мм, d4 = 25мм. Расход равен Q = 0,01м3\с, Относительная плотность жидкости δ= 0,95. Рассчитать давления p1, p2, p3, в соответствующих поперечных сечениях, имеющих координаты центров z1= 5м, z2 = 4м, z3 = 3м. Потерями напора можно пренебречь.
Задача 4
Согласно показанию манометра избыточное давление в закрытом резервуаре pизб= 4*106 Н/м2 Ось трубопровода находится на глубине h = 5 м от свободной поверхности (рис. 11). Коэффициенты местного сопротивления запорного крана ζ= 4, сопла ζ = 0,06. Линейным сопротивлением трубопровода можно пренебречь. Определить расход воды Q, если d1 = 10 см; d2 = 20 см; d3 =8 см.
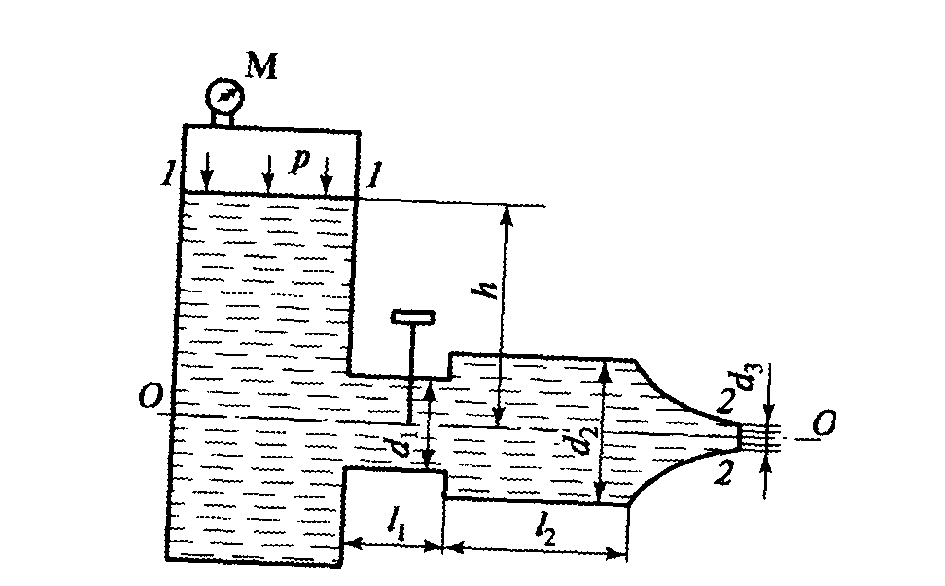
Рис.11
Задача 5
Рис. 12
Через трубопровод диаметром d = 100 мм движется вода с расходом Q = 8 л/с (рис. 12). С помощью U-образного ртутного манометра между сечениями 1—1 и 2—2, расположенными на расстоянии l = 50 м друг от друга, берется разность показаний h = 52 мм. Относительная плотность ртути ρрт = 13,6 т\м3 . Определить коэффициент потери напора на трение λ.
Вариант 5
Задача 1
Как изменится плотность бензина, если температура окружающей среды изменится с 20 °С до 70 °С.
Задача 2
Определить избыточное давление воды в трубе по показаниям батарейного ртутного манометра (рис. 13).
Рис.13
Отметки уровней ртути от оси трубы: z1 = 2,75 М; z2 = 4 М; z3 = 2,5 М;
z4 = 3,5 М; Плотность ртути ρрт = 13, 6 т \ м3, плотность воды ρрт = 1 т \ м3.
Задача 3
В стальном трубопроводе системы горячего водоснабжения диаметром d = 0,0125м длиной l =100м движется вода со скоростью v= 0,5 м\с. Температура воды 50 °С. На трубопроводе имеются два поворота на угол α = 90° и пробковый кран. Определить потери давления по длине.
Задача 4
Система из двух cсоединенных последовательно трубопроводов d1= 100 мм и d2 = 200 мм, l1= 200 м и l2 = 300 м соединяет Резервуары А и В, имеющие свободные поверхности на уровнях Н1 = 100 м и Н2 = 200 м (рис. 14). Коэффициенты потерь на местные сопротивления: ζ= 0,5; ζ = 0,1; ζ = 0,6; коэффициент трения на линейные сопротивления для сформировавшегося турбулентного режима λ = 0,02 + 0,5/d. Определить расход жидкости между резервуарами.
Рис.14
Задача 5
В сообщающихся сосудах находятся две несмешивающиеся жидкости с плотностями Р1 и Р2. Определить позицию свободных поверхностей жидкостей 111 и Н по отношению к плоскости сравнения О—О (рис. 15), если Р1 = 1000 кг/м, Р2 = 1200 кг/м, h= 11 см.
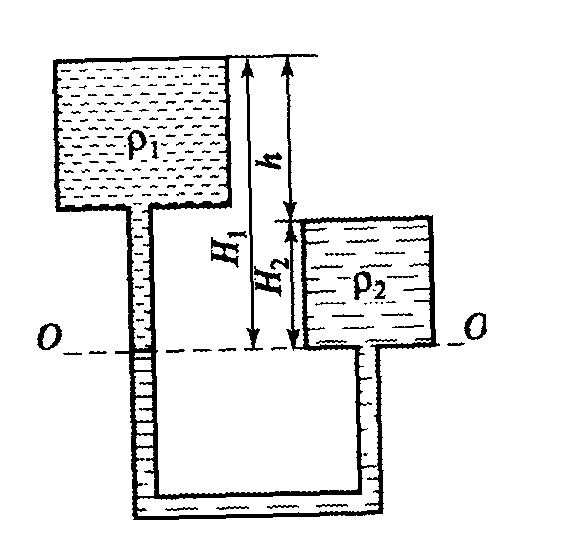
Рис. 15
Вариант 6
Задача 1
Трубопровод диаметром d = 500 мм и длиной L = 1000 м наполнен водой при давлении 400 кПа, и температуре воды 5 0C. Определить, пренебрегая деформациями и расширением стенок труб, давление в трубопроводе при нагревании воды в нем до 15 0C, если коэффициент объемного сжатия w = 5,18 10-10 Па-1, а коэффициент температурного расширения t = 150 10-6 0С-1.
Задача 2
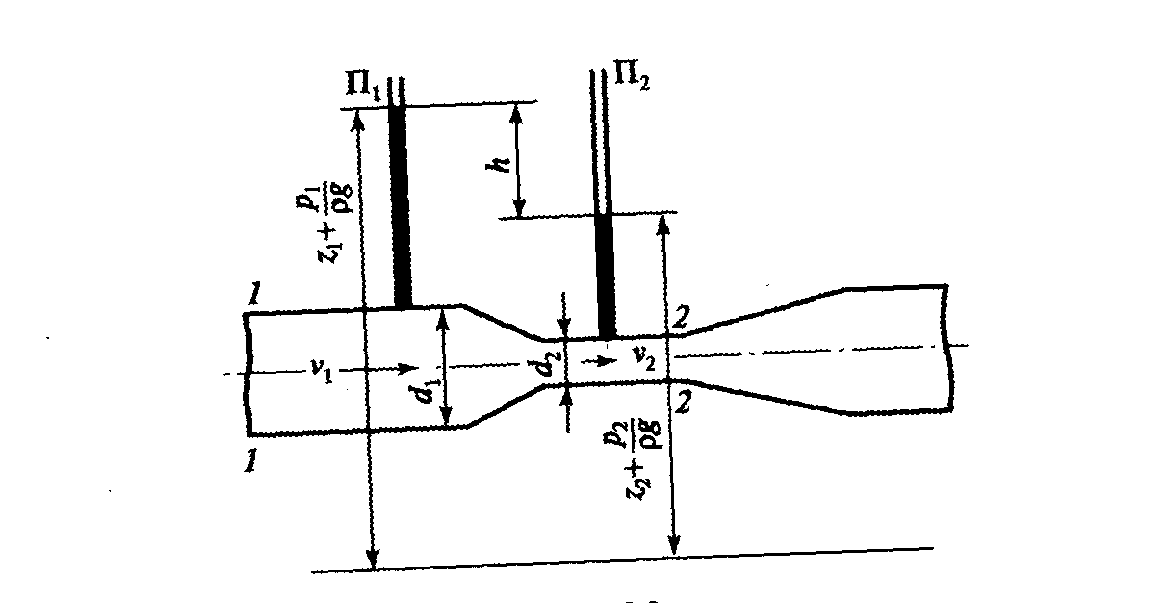
Рис.16
Вода протекает по водомеру Вентури, состоящему из трубы диаметром d1 = 20см, в которую вставлен участок трубы диаметром d2=10см. Пренебрегая сопротивлением, определить расход воды , если в пьезометрах П1 и П2 разность показаний h = 0,25м.
Задача 3
Определить объем воды и минерального масла в закрытом сосуде по данным пьезометра и индикатора уровня, если D = 0,4 м; a = 0,5 м; b = 1,6 м; ρм = 840 кг/м3 ρв = 1000 кг/м3, g = 10 м/с2 (рис. 17).
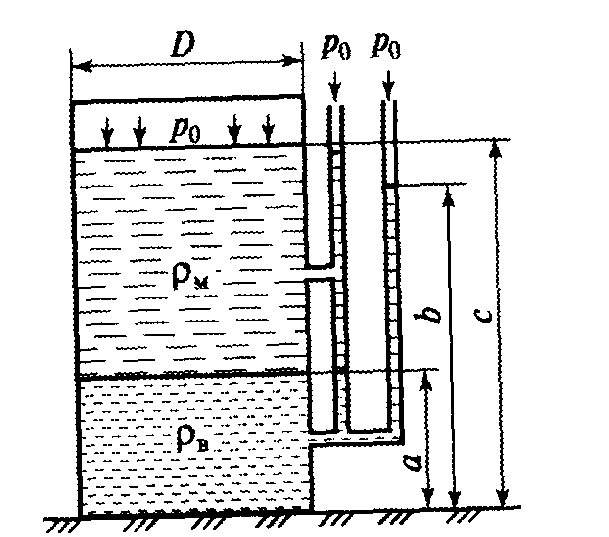
Рис.17
Задача 4
Двойная U-образная трубка заполнена двумя жидкостями таким образом, что свободная поверхность во внутреннем ответвлении трубки находится на одном уровне (рис. 18). Рассчитать плотность ρ2, если ρ1 = 1000 кг/м h1 = 0,8 м; h2 = 0,65 см.
Рис.18
Задача 5
Разность давлений между двумя горизонтальными цилиндрическими сосудами, наполненными водой и газом (воздухом), измерена с помощью дифференциального манометра, наполненного спиртом (Р2) и ртутью (р). Зная давление воздуха над свободной поверхностью воды в одном из сосудов, определить давление газа р, если рвозд = 2,5 . 10 Н/м; ρ1 = 1000 кг/м3; ρ2 = 800 кг/м3; ρ3= 13600 Н/м3; h = 200 мм; h2 = 250 мм; h1=0,5 м; g= 10 м/с (рис. 19).
Рис. 19
Вариант 7
Задача 1
Определить потери давления Δp в водяном тракте водонагревателя, состоящего из шестипетлевого стального трубчатого змеевика. Диаметр труб d = 0,075м, длина прямого участка l = 3м, петли соединены круговыми коленами, имеющими радиус R = 0,1м. расход воды Q = 0,01м3\с, температура 90 °С.
Задача 2
Рис.20
Несмешивающиеся жидкости с плотностями ρ1, ρ2 и ρ3 находятся в сосуде (рис. 20). Определить избыточное давление на основание сосуда ризб если ρ1 = 1000 кг/м3; ρ2 = 850 кг/м3; ρ3 = 760 кг/м3; h1 = 1 м; h2 =3 м; h3 = 6 м.
Задача 3
Какую силу нужно приложить к поршню 2, чтобы уравновесить действие силы Р1 действующей на поршень 1 диаметром а (рис. 21), если Р1 = 147 Н; D= 300 мм; d = 50 мм; h = 300 мм; ρ = 103 кг/м3; g = 10 м/с2.
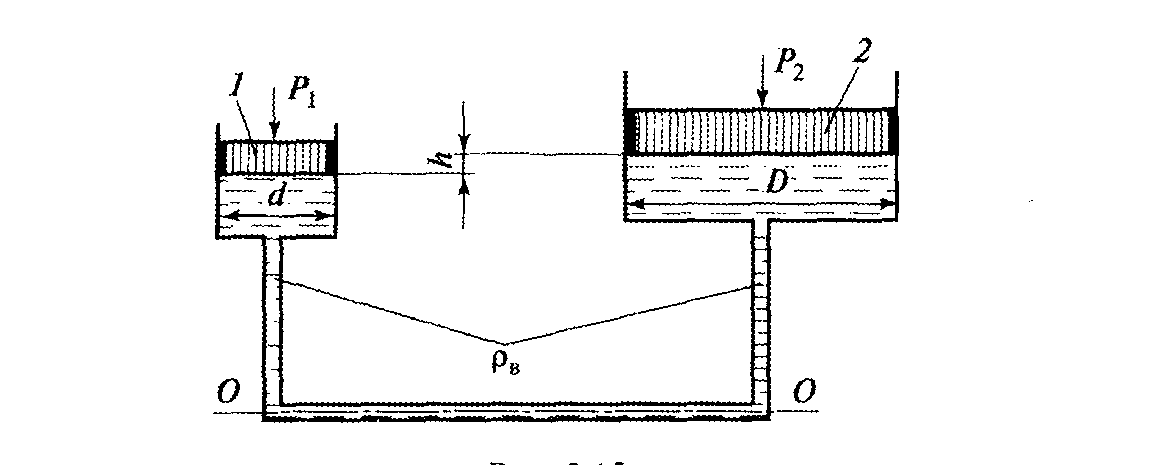
Рис. 21
Задача 4
Течение воды осуществляется из резервуара с постоянным уровнем Н = 16 м через короткий трубопровод, состоящий из отрезков труб с диаметрами d1 = 50 мм и d2 = 70 мм (рис. 22). На конце трубопровода помещено запорное устройство с коэффициентом местных потерь ζ= 4. другими потерями можно пренебречь. Определить расход воды Q.
‘
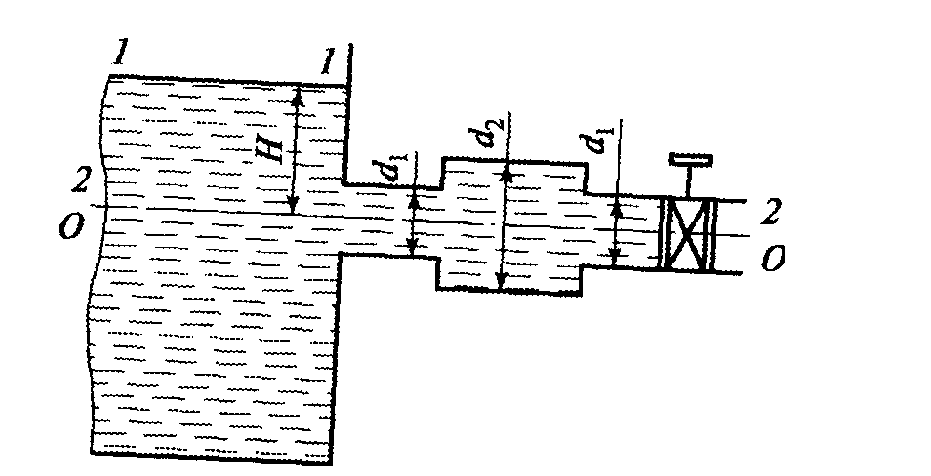
Рис.22
Задача 5
Система трех поршней в сообщающихся сосудах (рис. 23) находится в равновесии под действием трех сил Р1 Р2 Р3 (с учетом веса поршней). Площади поршней соответственно S1, S2, S3. Определить высоты h1 и h2, если Р1 = 1300 Н; Р2 = 1000 Н; Р3 = 800 Н; S1 = 0,4 м2; S2= 0,6 м2; S3 = 0,9 м2;
ρ = 1000 кг/м3; g= 10 м/с2.
Рис. 22
Вариант 8
Задача 1
Определить потери напора по длине при равномерном движении жидкости по трубопроводу со средней скоростью vср = 0,4м\с, если коэффициент кинематической вязкости жидкости υ= 0,4 * 10 -4 м2\с, диаметр трубопровода d= 100мм, его длина l=1000м
Задача 2
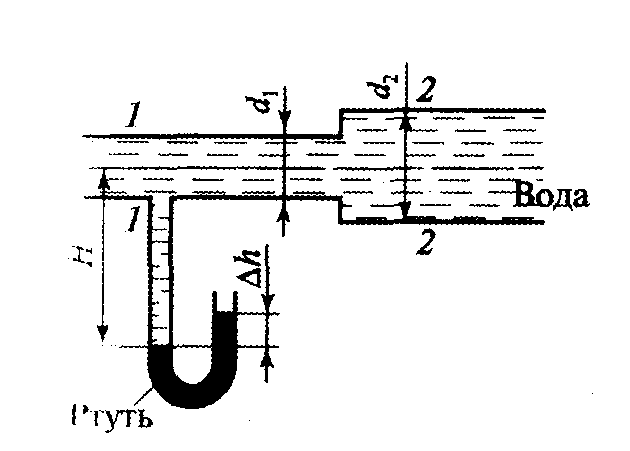
Рис.23
Последовательно соединенные трубопроводы с водой имеют U- образный ртутный манометр (рис. 23). Рассчитать давления и скорости воды в двух сечениях данных трубопроводов, пренебрегая всеми потерями напора, если Q = 10 л/с; d1 = 5 см; d2 =10 см; ρв = 103 кг/см ρрт = 13,6• 103 кг/м ΔН= 700 мм рт. ст.; Н= 1 м.
Задача 3
Весовой расход нефти плотностью ρ=880 кг\м3 с кинематической вязкостью υ= 1,1* 10-4 м2\с в горизонтальном трубопроводе диаметром d = 156мм длиной l= 2000м составляет G = 12*106 Н\сут. Определить давление p1 на входе в трубопровод, если давление на выходе p2 =15 Н\см2.
Задача 4
Два резервуара,
содержащие воду резервуар А закрыт
резервуар В открыт и связан с атмосферой.
Соединены с помощью трубопроводов с
диаметрами d1=
70 мм и d2
= 100 мм и длинам; l1
= 3м и l2
= 5 м (рис. 24). Разность уровней воды в
резервуара H=
5 м. Предположим что уровни 1—1 и 5—5
остаются постоянными. Определить расход
воды Q,
если рм
= 20 Н/см2
= 20*104 Н/м.
λ = 0,02; ζ 2=
0, 5; ζ3
=
;
ζ1=
1.
Рис.24
Задача 5
Система двух поршней находится в равновесии (рис. 25). Определить разницу показаний пьезометров h, если D/d= 3; Н= 2 м; p1 = p2 соnst
.
Рис. 25
Вариант 9
Задача 1
Расход воды при температуре 10 С в горизонтальной трубе кольцевого сечения, состоящей из двух концентрических стальных труб (при кольцевом расстоянии между трубами Кэ =0,15мм). Q = 0,0075м3\с. Внутренняя труба имеет наружный диаметр d = 0,075м, а наружная труба имеет внутренний диаметр D = 0,1м. определить потери напора на трение на длине трубы l = 300м.
Задача 2
Рис.26
Определить давление пара в цилиндре поршневого парового насоса (рис. 26, золотниковая коробка, обеспечивающая возвратно-поступательное движение поршня в паровом цилиндре, не показана), необходимое для подачи воды на высоту Н = 58 м, если диаметры цилиндров d1= 0,3 м; d2 = 0,18 м.
Задача 3
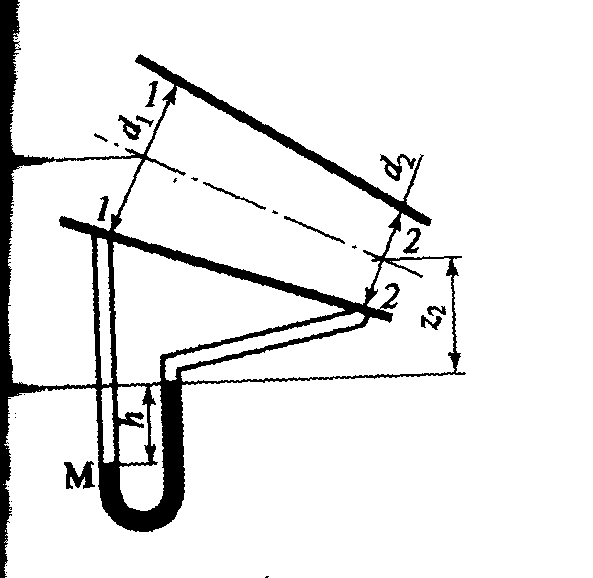
Рис.27
Расходомер Вентури расположен в наклонном труб проводе с диаметрами d1 = 0,25 м, d2 = 0,1 м (рис. 27). В двух сечениях ртутным манометром производится замер разности давлений. Зная разницу давлений h= 0,1 м ртутного столба, определить расход воды (ρрт = 13 600 кг/м3).
Задача 4
Манометр на трубопроводе, заполненном жидкостью, показывает давление 0,18 кгс/см2. На какую высоту H над точкой присоединения манометра поднимается в открытом пьезометре жидкость, находящаяся в трубопроводе, если эта жидкость: а) вода; б) четыреххлористый углерод?
Задача 5
Запаянная с одного конца цилиндрическая трубка длиной 18м вертикально погружается открытым концом в воду до тех пор, пока ее запаянный конец не окажется на одном уровне с поверхностью воды. Когда температура воздуха в трубке и воды уравнялась, оказалось, что воздух стал занимать половину прежнего объема. Определить температуру воды, если начальная температура воздуха в трубке 27°С. Атмосферное давление 105 Па.
Вариант 10
Задача 1
По прямому горизонтальному трубопроводу длиной l = 150 м необходимо подавать Q=10 м3/ч жидкости. Допускаемая потеря напора 10 м. Определить требуемый диаметр трубопровода, принимая коэффициент трения λ = 0,03.
Задача 2
Рис.25
Два закрытых сосуда содержат воду. Свободные поверхности расположены по отношению к плоскости сравнения О—О на высотах h1 = 1 м и h2 = 1,8 м (рис. 28). Показание манометра p1 = 1,2 10 Н/м2, Разница уровней ртути в дифференциальном манометре Δh = 200 мм. Определить давление на свободную поверхность второго резервуара p2.
Задача 3
В напорный бак с площадью поперечного сечения S = 3 м2 притекает вода. В дне бака имеется сливное отверстие. При установившемся течении расход через отверстие равен притоку и уровень воды устанавливается на высоте h = 1 м. Если прекратить приток воды, через 100 с бак опорожнится. Определить приток воды в бак.
Задача 4
Показание манометра, расположенного на расстоянии h = 1 м от днища резервуара, р1 = 5 Н/см2. Определить высоту свободной поверхности бензина Н в резервуаре (рис. 28), если рв=850 кг/м3 g = 10 м/с2.
Рис.28
Задача 5
Сосуд содержит две Несмешивающиеся жидкости с плотностями ρ и ρ (рис. 29). давление над свободной поверхностью измеряется манометром. Определить избыточное давление на основание сосуда, если рм = 102 Н/м ρ1 = 890 кг/м3; ρ2 = 1280 кг/м3; h1 = 2,1 м; h2=2,9 м; g = 10 м/с2.
Рис. 29
ПРИЛОЖЕНИЕ 1
Некоторые физические свойства жидкостей при давлении 0,1 Мпа
Жидкость |
Температура, 0С |
Плотность, кг/м3 |
Удельный вес, Н/м3 |
Вязкость 104,м2/с |
||
Бензин |
авиационный |
20 |
739-780 |
7250-7652 |
0,49 для 20 0С |
|
автомобильный |
712-761 |
6980-7470 |
||||
Масло |
веретенное АУ (ГОСТ 1642-75) |
50 |
888-896 |
8711-8790 |
||
для гидравлических систем АМГ-30 (ГОСТ 6794-75) |
850 |
8340 |
||||
индустриальное общего назначения без присадок (ГОСТ 20799-75) |
И-5А |
890 |
8731 |
0,04-0,06 |
||
И-8А |
900 |
8829 |
0,06-0,08 |
|||
И-12А |
880 |
8633 |
0,10-0,14 |
|||
И-20А |
885 |
8682 |
- |
|||
И-25А |
890 |
8731 |
0,24-0,27 |
|||
И-30А |
890 |
8731 |
0,28-0,33 |
|||
И-40А |
895 |
8780 |
0,35-0,45 |
|||
И--100А |
920 |
9025 |
0,90-1,18 |
|||
соляровое |
20 |
885-902 |
8680-8850 |
|
||
трансформаторное |
50 |
886 |
8692 |
|
||
турбинное (ГОСТ 32-74) |
22 |
900 |
8829 |
|
||
30 |
900 |
8829 |
0,28-0,36 |
|||
46 |
900 |
8829 |
0,44-0,48 |
|||
ПРИЛОЖЕНИЕ 2
Кинематическая вязкость масел при различных температурах
Масло |
104, м2/с при 0С |
|||||||
100 |
50 |
10 |
0 |
-5 |
-10 |
|||
веретенное АУ (ГОСТ 1642-75) |
0,036 |
0,13 |
0,90 |
1,80 |
2,80 |
4,40 |
||
для гидравлических систем АМГ-30 (ГОСТ 6794-75) |
0,047 |
0,11 |
0,30 |
0,44 |
0,54 |
0,67 |
||
индустриальное (ГОСТ 20799-75) |
И-20 |
0,048 |
0,18 |
1,13 |
2,75 |
4,20 |
6,40 |
|
И-45 |
0,081 |
0,42 |
5,01 |
11,90 |
19,50 |
59,90 |
||
И-50 (машинное СУ) |
0,085 |
0,50 |
8,33 |
22,90 |
41,70 |
83,80 |
||
трансформаторное с присадкой ионол |
0,030 |
0,09 |
0,05 |
0,89 |
1,24 |
1,77 |
||
турбинное (ГОСТ 32-74; 9972-74) |
ТП-22 |
0,060 |
0,22 |
2,13 |
4,76 |
7,73 |
9,10 |
|
ТП-22 (из сернистых нефтей) |
0,050 |
0,21 |
1,72 |
3,75 |
5,68 |
25,30 |
||
ТП-30УТ |
0,060 |
0,42 |
3,59 |
8,63 |
14,40 |
33,10 |
||
ПРИЛОЖЕНИЕ 3
Динамическая вязкость масел при различных температурах
Жидкость |
0C |
10-1 Па с при давлении МПа |
|||||
0,1 |
10 |
20 |
30 |
40 |
50 |
||
Автол |
37 |
1,440 |
1,940 |
2,450 |
3,030 |
3,672 |
4,896 |
Машинное |
22 |
2,880 |
3,416 |
4,176 |
5,184 |
6,822 |
8,640 |
Трансформаторное |
22 |
0,346 |
0,374 |
0,418 |
0,489 |
0,562 |
0,650 |
ПРИЛОЖЕНИЕ 4
,
где p – абсолютное давление, равное 101325 Па; T – абсолютная температура; R – удельная газовая постоянная, Rвозд = 287 Дж/кг К, Rгаза = 334 Дж/кг К
СПИСОК ЛИТЕРАТУРЫ
1. Чугаев Р. Р. Гидравлика. – Л.: Энергия, 1982. – 672 с.
2. Угинчус А. А., Чугаева Е. А. Гидравлика – Л.: Стройиздат, 1971. – 350 с.
3. Альтшуль А. Д., Киселев П. Г. Гидравлика и аэродинамика. – М.: Стройиздат, 1975 – 323 с,
4. Константинов Н. М., Петров Н. А., Высоцкий Л. И. Гидравлика, гидрология и гидрометрия: В 2-х частях. Ч. 1. Общие законы. – М.: Высшая школа, 1987. – 304 с.
5. Гидравлика, гидромашины и гидроприводы / Башта Т. М., Руднев С. С., Некрасов Б. Б. и др. – М.: Машиностроение, 1982. –422 с.
6. Юшкин В. В. Гидравлика и гидравлические машины. – Минск: Вышейшая школа, 1974. – 270 с.
7. Угинчус А. А. Гидравлика гидромашины и гидроприводы. – Л.: ГЭИ, 1970. – 390 с.
8. Примеры гидравлических расчетов / Под ред. Н. М. Константинова. – М.: Транспорт, 1987. – 498 с.
9. Справочное пособие по гидравлике, гидромашинам и гидроприводам / Под общей ред. Б. Б. Некрасова. – Минск: Вышейшая школа, 1985. –365 с.