2. Анализ адекватности уравнения и значимости найденных коэффициентов уравнения. Отбраковка незначимых факторов.

В верхней части табл.1 приведены данные регрессионной статистики. Множественный R = 0,984896 и стандартная ошибка - 0,049782, что свидетельствует о высокой степени совпадения вычисленных значений Х (по приведенному ниже уравнению регрессии) с экспериментальными значениями Х.

Оценка адекватности уравнения приведена в дисперсионном анализе. Высокая величина F=129,4203 и низкое значение Значимость F =4,54E-17, что меньше уровня значимости 0,05, указывают на адекватность уравнения регрессии.

В нижней части табл.1 выведены итоги расчета свободного коэффициента регрессии (Y-пересечение) и коэффициентов регрессии, стоящих перед аргументами NaCl , Mg²⁺, Ca²⁺ , SO₄^2- , Br^- и н.о.

Исходя из результатов расчетов уравнение регрессии выглядит следующим образом:

Х=100,0939-0,88232*NaCl-4,56825*Mg²⁺-22,915*Ca²⁺-3,07422*SO₄^2--93628*Br^-+0,371221* н.о.

Проверим значимость вычисленных коэффициентов регрессии. Значимость коэффициентов определяется по величине Р-значений, приведенных для каждого коэфициента в отдельном столбце. Коэффициенты уравнения значимы в том случае, если Р-значение меньше 0,05 (уровня значимости). Из анализа величин Р-значений видно, что условию значимости отвечают коэффициенты Y-пересечение, и коэффициенты, стоящие перед аргументами NaCl .

3.Уточненные вычисления коэффициентов уравнения регрессии, вывод графиков подбора и остатков.

Для нахождения уточненного уравнения регрессии выполняют повторные вычисления, принимая в расчет исходных экспериментальных данных только значимые столбцы аргументов NaCl , функцию Х (столбцы №1, 2).

Выводимые программой Microsoft Excel результаты уточненных расчетов коэффициентов регрессии, регрессионной статистики и дисперсионного анализа

Таблица 2.

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,960387
R-квадрат	0,922343
Нормированный R-квадрат	0,919665
Стандартная ошибка	0,072887
Наблюдения	31
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	1	1,82981	1,82981	344,4374	1,23E-17
Остаток	29	0,154061	0,005312
Итого	30	1,983871
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	99,89238	0,072394	1379,849	2,07E-71	99,74431	100,0404	99,74431	100,0404
NaCl	-1,11405	0,060027	-18,559	1,23E-17	-1,23682	-0,99128	-1,23682	-0,99128

Величины расхождений расчетных и экспериментальных

значений (остатков) величины Х

Таблица3.

№ Наблюдение	Расчетная (предсказанная величина) X, доля	Остатки
1	98,71148	0,088518
2	98,82289	0,077113
3	98,77832	0,021675
4	98,70034	-0,00034
5	98,48867	0,111328
6	97,61971	0,080287
7	98,45525	0,04475
8	98,67806	0,02194
9	98,42183	0,078171
10	98,56666	0,033345
11	98,62236	0,077642
12	98,61122	0,088783
13	98,77832	-0,07832
14	98,75604	-0,05604
15	98,71148	-0,01148
16	98,67806	0,02194
17	98,77832	0,021675
18	98,64464	-0,04464
19	98,1656	-0,1656
20	98,48867	-0,08867
21	98,60008	-7,7E-05
22	98,53323	0,066766
23	98,67806	-0,07806
24	98,23244	-0,13244
25	98,77832	-0,07832
26	98,48867	0,011328
27	98,55551	-0,05551
28	98,70034	-0,10034
29	98,18788	0,012122
30	98,75604	0,043956
31	98,71148	-0,01148

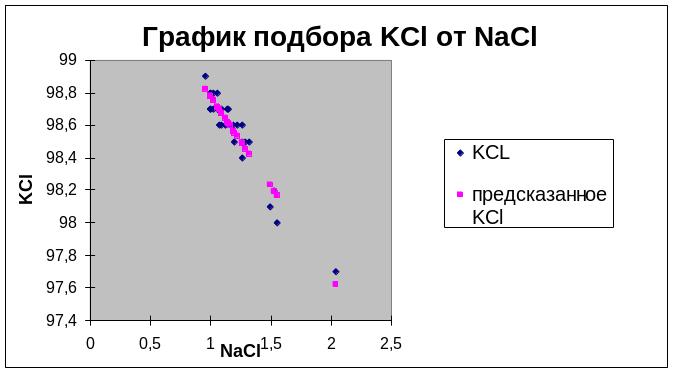
Рис.1