Задача № 7

Построить пересечение сферы (с центром в точке O и радиусом R) с призматическим отверстием ABCD. Решение задачи показать в трех проекциях. Данные берут из таблицы 4.

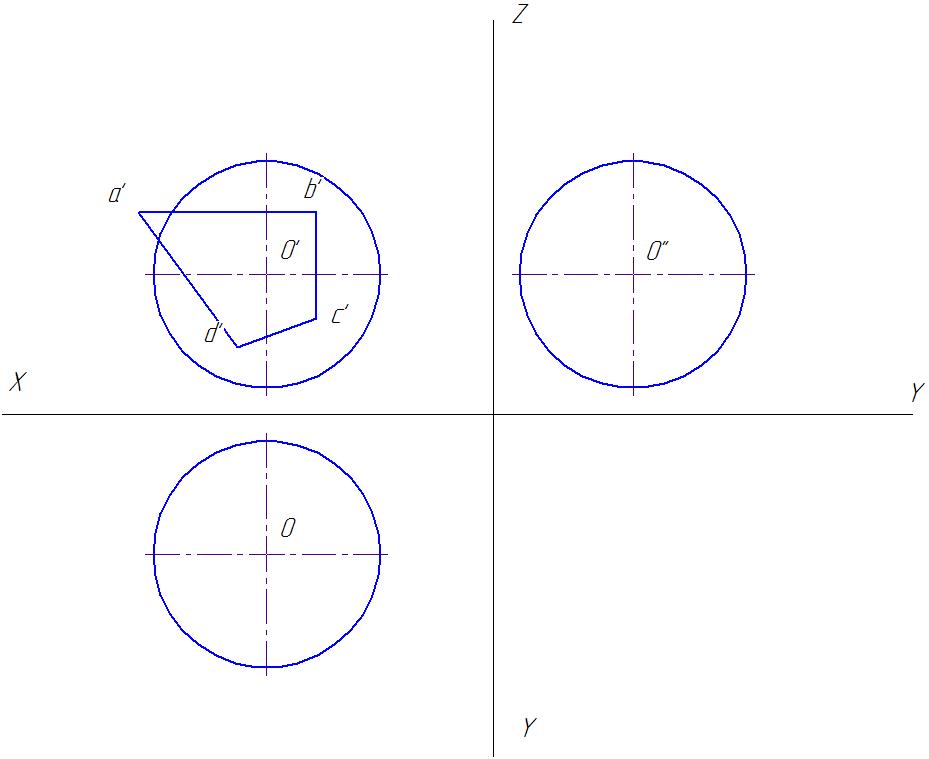
Указания к решению задачи № 7.

Вырожденная фронтальная проекция сквозного отверстия представлена четырехугольником ABCD. Задача сводится к построению линии пересечения граней четырехугольника ABCD с поверхностью сферы. В сечении плоскости со сферой всегда получается окружность, которая может проецироваться или в окружность, или в эллипс, в зависимости от положения ее плоскости по отношению к плоскости проекций. Обратить особое внимание к нахождению точек кривых, определяющих границы видимости кривых и точки касания эллипсов с очерковыми окружностями сферы.

Таблица 4. Данные к задаче № 7

Номер варианта	XО	Yo	ZО	XA	ZA	XВ	ZВ	XС	ZС	XD	ZD	R
1	70	60	60	20	30	60	90	95	60	95	30	48
2	70	60	60	20	30	60	70	110	70	95	30	48
3	70	60	60	20	30	45	70	45	95	95	30	48
4	70	60	60	40	30	40	70	80	70	120	30	48
5	70	60	60	40	30	40	50	80	95	120	30	48
6	70	60	60	40	30	80	90	95	90	120	30	48
7	70	60	60	35	50	80	90	110	90	110	50	48
8	70	60	60	35	50	60	90	110	60	110	50	48
9	70	60	60	35	50	35	80	60	100	120	50	48
0	70	60	60	120	95	45	95	100	30	120	70	48

Пример решения задачи

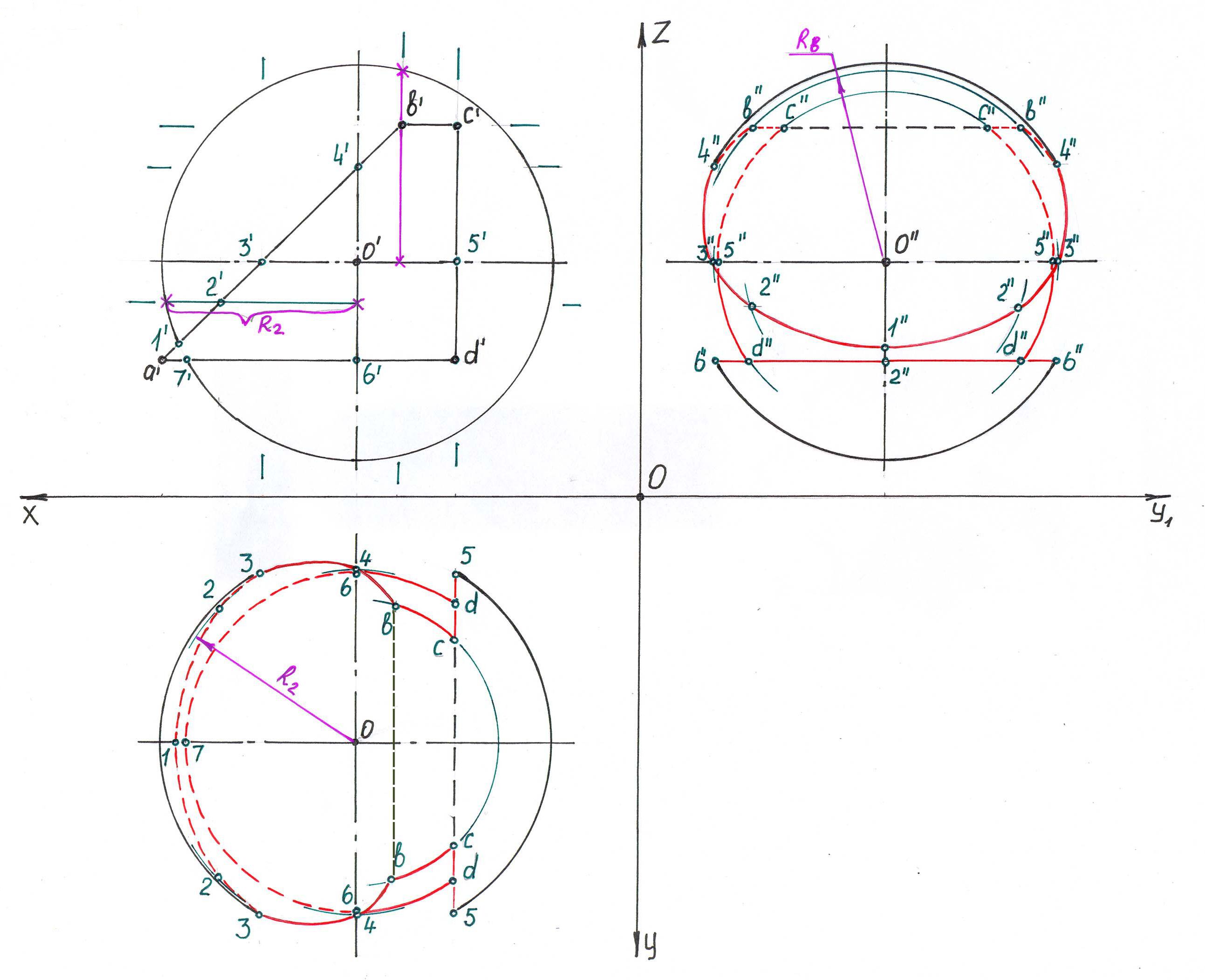
Последовательность решения

1. По координатам находим центры сферы на трех проекциях и заданным радиусом R достраиваем проекции сферы. По координатам точек выстраиваем на фронтальной плоскости проекций контур призматического отверстия а'b'c'd'.

2. Отмечаем характерные точки пересечения очерковых образующих двух фигур – точки 1' и 7'. Далее отмечаем точки пересечения призмы с осями сферы – точки 3', 4', 5' и 6'. Точку 2' берем произвольно для более точного построения кривой. Можно было также отметить дополнительную точку между точками 3' и 4'. Грани призмы, расположенные параллельно соответствующей плоскости проекций, проецируются на нее в виде окружности, а наклонные грани будут представлены в виде эллипса, для построения которого и требуются дополнительные точки.

3. Строим проекции точек на горизонтальной плоскости проекций: точки 1 и 7 будут лежать на оси (на экваторе), так как они лежат на очерковой образующей сферы. Точки 3 и 4, наоборот, будут лежать на очерковой образующей, так как на фронтальной плоскости проекций они лежат на горизонтальной оси (на экваторе). Так как отверстие сквозное, то точки будут дублироваться. Остальные точки находим с помощью вспомогательных проецирующих плоскостей, которые строятся через точки призмы параллельно горизонтальной плоскости проекций (׀׀ оси ОХ). Радиус для точки замеряется от вертикальной оси сферы до ее очерковой образующей, (смотри R₂). На горизонтальной плоскости проекций выстраиваем вспомогательную окружность (проекцию секущей плоскости) и сбрасываем на нее точки. Так выстраиваем точки: 2, 4, b, c, d и 6.

4. Построенные точки соединяем между собой в той же последовательности, как они обозначены на контуре призматического отверстия, т. е. 1 – 2 – 3 – 4 – b – c – 5 – d – 6 – 7.

5. Определяем видимость линии пересечения. Сначала удаляем часть очерковой образующей сферы от точки 3 до точки 5, так как на фронтальной плоскости проекций горизонтальная ось (экватор сферы) попадает в призматическое отверстие (участок 3'5'). Смотрим сверху на сферу (на фронтальной плоскости проекций): все точки, расположенные над горизонтальной осью сферы, будут видимыми, под осью сферы – невидимыми на горизонтальной плоскости проекций. Соответственно, линия 34bc5 будет видимой, но и часть линии 5d67 тоже будет видимой, так как она выступает за контур линии 34bc5 (точки d, 6, 7 лежат на большем радиусе, чем точки b, c).

6. На профильной плоскости проекций точки строят таким же способом, только вспомогательные плоскости проводят параллельно профильной плоскости проекций (или ׀׀ оси OZ). При определении видимости на сферу смотрят слева (на фронтальной плоскости проекций): точки, лежащие до вертикальной оси слева, будут видимыми, за ней – невидимыми. Вспомогательные окружности строят из центра сферы О' на профильной плоскости проекций.