2 Вопрос

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

 Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x₀ + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

х = x₀ - vt

Уравнение скорости выражает зависимость скорости тела от времени v = v(t). Уравнение v(t) служит для описания движение тела. Помимо значений скорости для каждого момента времени по уравнению v(t) всегда можно найти основные кинематические величины - ускорение и перемещение тела, например: У равнение скорости при равноУскоренном движении. У равнение скорости при механических гармонических колебаниях.	v - мгновенная скорость; конечная скорость в равноускоренном движении	м/с
	v0 - начальная скорость в равноускоренном движении	м/с
	s - перемещение тела	м
	t - время движения	с
	a - ускорение	м/с2
	А - амплитуда колебаний, А = хмакс	м
	ω - циклическая частота колебаний	1/с
	х - координата тела	м
	φ0 - начальная фаза колебаний	рад

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:

v_cp = v

Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t:

= / t

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

= • t

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

v_x = v, то есть v > 0

Проекция перемещения на ось ОХ равна:

s = vt = x – x₀

где x₀ – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x₀ + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

х = x₀ - vt

Равнопеременное движение - это движение, при котором скорость точки (тела) за любые равные промежутки времени изменяется на одну и ту же величину. Если это движение происходит по прямой, то это прямолинейное равнопеременное движение.

Изменение скорости в единицу времени называется ускорением. Обычно оно обозначается латинской буквой "a".

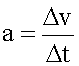где дельта-v - изменение скорости, произошедшее за время дельта-t.

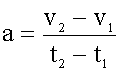
Ускорение "a" - величина векторная. При прямолинейном движении ее направление зависит от знака изменения скорости дельта-v. Принято считать, что направление координатной оси для ускорения "a" совпадает с направлением координатной оси для скорости. В этом случае, при разгоне ускорение положительно, при торможении - отрицательно.

При решении задач всегда рассматриваются не сами вектора ускорения, скорости и перемещения, а их проекции на координатные оси.

Формулы для решения:

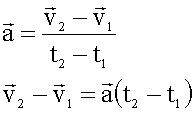
Если начальная скорость в начальный момент времени равна нулю, то есть, ,

то

Пройденный путь (с учетом его направления), а при прямолинейном движении - перемещение:

Равнопеременное Прямолинейное Движение

Для этого случая, как и для предыдущего, достаточно выбрать одну из осей координат и направить ее вдоль траектории движения.

Положение материальной точки также будет описываться уравнением движения:

х = f_t(t) или у = f₂(t), или z = f₃(t).

Равнопеременным движением называют такое движение, при котором ускорение есть величина постоянная ( а = const). Направление вектора ускорения при этом может совпадать с направлением начальной скорости движения или же быть направлено в противоположную сторону.

Если на каком-то отрезке времени скорость и ускорение совпадают по направлению, то движение называется равноускоренным, если же на данном отрезке времени эти векторные величины имеют противоположные направления - движение называется равнозамедленным.

Итак, при равнопеременном прямолинейном движении ускорение есть величина постоянная:

Отсюда следует:

Если отсчет времени вести от нуля, а начальную скорость соответственно обозначить v₀, то можно записать:

Соответственно в проекциях на ось Ох:

v_x; v₀ ; a_x могут быть как положительными, так и отрицательными числами. Если знаки величин v₀ и а_х совпадают - движение равноускоренное, если они различны - движение равнозамедленное (при t, близких к нулю). Например, уравнения v_x = 3 + 2t или v_х = -1 - 3t - описывают равноускоренные движения.

Уравнения v_х = 3 - 2t или v_х = -2 + 3t при достаточно малых t показывают, что движения являются равнозамедленными.

Из уравнений ясно, что зависимость проекции скорости от времени является линейной, так как независимая переменная t входит в уравнение первой степени.

Чтобы вывести формулу зависимости координаты от времени для этого вида движения, обратимся к графику скорости.

Для случая, при котором V₀равно нулю, получаем зависимость v = at, где перемещение численно равно заштрихованной площади (рис. 10).

Отсюда

Если же v₀ не равно 0, то перемещение будет равно площади трапеции, которая может быть представлена суммой площадей прямоугольника и треугольника (рис. 11).

Нетрудно доказать, что

Если перемещение по оси Ох представить как (х - х₀), то получим:

Для определения вида движения следует применить прежнее правило: если совпадают знаки у v₀ и а_х - движение равноускоренное, в противном случае - движение в начальный момент является равнозамедленным.

Указание на начальный момент означает, что при несовпадении знаков у v₀ и а_х рано или поздно движение все же станет равноускоренным, так как изменение скорости приведет в конечном итоге к тому, что ускорение и скорость будут совпадать по направлению. Например, при движении брошенного вверх тела сначала его скорость по своему направлению противоположна ускорению свободного падения. Движение при этом будет равнозамедленным. Скорость убывает, становится равной нулю и затем меняет свое направление (после того, как тело достигнет наивысшей точки полета). Далее движение становится равноускоренным.

При этом ускорение остается величиной постоянной и по модулю, и по направлению. Сформулируем основную и обратную задачи механики. Основная задача. Определить местоположение материальной точки в любой заданный момент времени. Чтобы ее решить, необходимо составить уравнения движения: х = f_t(t); у = f₂(t); z = f₃(t).

Обратная задача. Зная местоположение тела в любой заданный момент времени, определить характеристики его движения (v и a). Графически равнопеременное прямолинейное движение можно изобразить графиком зависимости проекции ускорения от времени (рис. 12).

Движения 1, 2, 3 являются равнопеременными. Не зная начальных скоростей, нельзя судить о том, являются ли эти движения равнозамедленными или равноускоренными.

Ясно только одно: а₁ и а₂ совпадают по направлению с выбранной осью Ох, а а₃ направлено в противоположную сторону. Графики скорости дают более конкретные сведения о движении тела (рис. 13): Движения 1 и 2 - равноускоренные с ускорениями а₂>а,. Движения 3 и 4 - равнозамедленные с ускорениями а₃ > а₄

Из графика зависимости проекции скорости от времени можно получить более точные сведения о движении.

Так, из рис. 14 видно, что при равнозамедленном движении проекция скорости v_х при времени t₁ обратилась в ноль, а затем модуль скорости стал возрастать, а знак проекции изменился, следовательно, движение с этого момента стало равноускоренным.

Нетрудно заметить, что на графике скорости ускорение будет равно тангенсу угла наклона графика к оси времени (рис. 14).

Поскольку в уравнение проекции перемещения (координаты) время входит во второй степени, то соответствующий график должен быть параболой (рис. 15).

Проанализируем различные движения, отображенные на графиках х = f(t) (рис. 15 и 16).

Графики на рис. 15 соответствуют условиям:

При более общих условиях возможны следующие случаи (рис. 16):

1. Движение равноускоренное: а_х > 0; v_0x > 0; х₀ > 0.

2. Движение равноускоренное: а_х < 0; v_0x < 0; х₀ > 0.

3. Движение равноускоренное: а_х < 0; v_0x, < 0; х₀ > 0.

4. Движение равнозамедленное: v_0x > 0; а_х < 0, конечная координата не меняется с течением времени, что означает остановку.

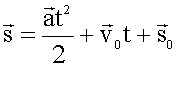
Если начало отсчета времени и начало пути совпадают, то

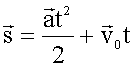
Если начальная скорость равна нулю, то

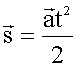
Все эти формулы справедливы в проекциях на любые координатные оси и при решении задач используются именно уравнения в проекциях: