33) Вычитающие двоичные счетчики.

Реверсивный счётчик может работать в качестве суммирующего и вычитающего

Суммирующий счётчик, как было показано выше, получается при подсоединении к входу последующего каскада прямого выхода предыдущего.

Каждый входной импульс увеличивает число, записанное в счётчик, на 1. Перенос информации из предыдущего разряда в последующий происходит при смене состояния предыдущего разряда (триггера) с 1 на 0.

Вычитающий счётчик подучается при подсоединении к входу последующего каскада инверсного выхода предыдущего. Он действует обратным образом: двоичное число, хранящееся в счётчике, с каждым поступающим импульсом уменьшается на 1.

Перенос из младшего разряда в старший имеет место при смене состояния младшего разряда с 0 на 1.

Переполнение происходит после достижения счётчиком нулевого состояния, при этом в счётчик записывается максимально возможное значение, т. е. во все разряды – единицы.

Путём включения в схему двоичного суммирующего счётчика (рисунок 60), дополнительных ЛЭ, переключающих на вход последующего триггера прямого и инверсного выходов предыдущего, подучается схема реверсивного счётчика. Фрагмент схемы реверсивного счётчика приведён на рисунке 61.

Рисунок 61 Фрагмент схемы реверсивного счётчика

Схема имеет два входа для подачи входных сигналов: +1 – при работе в режиме суммирования, - 1 – при работе в режиме вычитания. Дополнительный управляющий вход N задаёт направление счёта. При N=0 схема (рисунок 61) работает как суммирующий счётчик, а при N=1 – как вычитающий.

34) Реверсивные счетчики, 4-х разрядный реверсивный счетчик на Т-триггере

Для построения вычитающего счетчика достаточно подать сигнал переноса на триггер старшего разряда не с прямого выхода предыдущего триггера, а с инверсного.

Связи между триггерами реверсивного счётчика соответствуют как суммирующему, так и вычитающему счётчику, но работает только одна из связей, которая определяется командой «Реверс» и подается на элемент И–НЕ, включенные в цепи передачи сигнала переноса.

35)Десятичные счетчики.

36)Счетчик с произвольным модулем счета на jk – триггере.

37) Счетчики с принудительным насчетом сигналов

38)Делители частоты.

Счетчиками в цифровой технике называются специальные элементы, позволяющие подсчитывать число поступивших на вход импульсов. Понятие «счетчик импульсов» тесно связано с понятием «делитель частоты». По сути дела, это одно и то же устройство. Но рассмотрим все по порядку.

В качестве простейшего делителя частоты может выступать рассмотренный в предыдущей главе Ж-триггер (см. рис. 1.19). Для того, чтобы этот триггер работал как делитель, нужно на оба входа J и К подать высокий логический уровень. Теперь, если на вход С подать импульсный сигнал некоторой постоянной частоты, то по спаду каждого входного импульса триггер будет переключаться в противоположное состояние.

В результате на выходе JK-триггера мы получим другой сигнал с частотой следования импульсов в два раза меньшей, чем частота импульсов на его входе. Этот процесс наглядно показан на рис. 1.20. Как видно из рисунка, период сигнала на выходе делителя ровно в два раза больше периода входного сигнала. А частота выходного сигнала, соответственно, в два раза ниже входного.

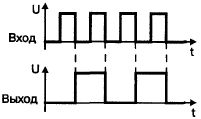
Рис. 1.20. Деление частоты

Второй вариант делителя частоты приведен на рис. 1.21. Он построен на основе D-триггера. Для того, чтобы перевести D-триггер в_счетный режим, нужно соединить инверсный выход триггера Q с его D-входом, так как это показано на рис. 1.21. Теперь, если подать сигнал на вход С, такая схема тоже будет работать как делитель. Выходной сигнал такого делителя снимается с выхода Q триггера.

Рассмотрим подробнее работу этой схемы. Предположим, что после включения триггер установился в единичное состояние. Это означает, что на инверсном выходе триггера (Q) присутствует логический ноль. Этот ноль поступает на D-вход. Подадим на вход делителя некоторый цифровой сигнал, такой же, как мы подавали и в предыдущем случае (см. рис. 1.20).

По спаду первого входного импульса D-триггер перейдет в нулевое состояние, так как на его D-входе сигнал логического нуля. После этого на инверсном выходе триггера устанавливается логическая единица. Поэтому по спаду следующего входного импульса триггер переключится в единичное состояние. И так далее.

Результат работы делителя на D-триггере точно такой же, как и делителя на JK-триггере, и выходной сигнал нового варианта так же полностью соответствует рис. 1.20. Следует заметить, что в настоящее время Ж-триггеры применяются довольно редко. Гораздо большее распространение благодаря своей простоте и универсальности получили D-триггеры.

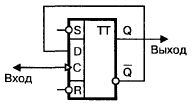
Рис. 1.21. Простейший делитель частоты

Делители широко используются в цифровой технике. Цепочка последовательно соединенных D-триггеров позволяет получить сигналы требуемой частоты путем деления импульсов задающего генератора.

Пример. Соединенные последовательно два делителя позволят получить сигнал с частотой в четыре раза меньшей, чем входная. Трехкаскадный делитель (три последовательно соединенных D-триггера) дадут деление на восемь. Четыре каскада будут делить на шестнадцать. И так далее.

На рис. 1.22 изображена схема четырехкаскадного делителя частоты на D-триггерах. Импульсы тактового генератора поступают на вход первого каскада деления. Если частота сигнала на входе равна f, то на выходах делителя мы получим сигналы со следующими частотами:

Q0 — f/2;          Q1 —f/4;           Q2 —f/8;               Q3 — f/16.

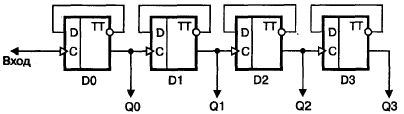
Рис. 1.22. Четырехкаскадный делитель частоты