
- •1)Обобщенная схема цвм.
- •2)Автомат Мура.
- •3)Основы анализа логических схем с обратными связями.
- •4)Анализ логических схем с помощью карт Карно.
- •7)Элементарные автоматы. Элементарные автоматы с одним входом.
- •8)Элементарные автоматы с двумя входами.
- •9)Обобщенная схема цифрового автомата.
- •10) Синтез комбинационных схем с помощью сднф и диаграмм Вейча.
- •11)Синтез цифровых автоматов.
- •Дешифраторы (декодеры)
- •15,16) 15 И 16 билеты совместно, про rs – триггеры на и элементах в 5 билете.
- •17)Серии цифровых логических микросхем (мс). Мс выключающие триггеры.
- •18)Синтез триггерных схем.
- •19)Д-триггер.
- •20)Т-триггер.
- •21)Jk-триггер.
- •22)Двойные триггеры.
- •23)Синтез двойного jk-триггера на элементах “и-не”.
- •24)Синтез двойного jk-триггера на элементах “или-не”.
- •25)Синхронный rs-триггер с динамическим управлением.
- •26)Синхронный jk-триггер с динамическим управлением.
- •27)Синтез синхронных триггеров со статическим управлением.
- •28)Регистры.
- •29) Регистр к555ир1
- •30) Регистр с тремя выходными состояниями. Кр 1804 ир1.
- •31) Счетчики. Двоичные суммирующие счетчики с последовательным переносом.
- •33) Вычитающие двоичные счетчики.
- •35)Десятичные счетчики.
- •36)Счетчик с произвольным модулем счета на jk – триггере.
- •37) Счетчики с принудительным насчетом сигналов
- •39)Делители частоты с модулем деления на 3.
- •40)Сумматоры. Сумматор на регистрах и кс суммирования.
- •43)Основные элементы памяти.
- •44)Организация памяти в вычислительной технике.
- •45) Дешифраторы. 3-х разрядный дешифратор на элементах “и”.
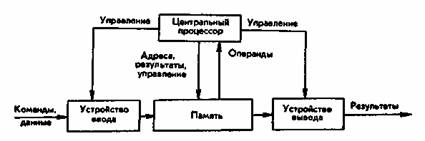
1)Обобщенная схема цвм.
Определение электронной вычислительной машины (с учетом программного принципа управления) предполагает, что ЭВМ строится по следующей схеме (рис. 1.2).
Определение конечного автомата.
Конечный автомат – дискретный автомат, в котором переход из одного состояния в любое другое может быть совершено за конечное число шагов (таким автоматом, например, является процессор).
Схему конечного автомата удобно представлять в виде комбинационной схемы, реализующей характеристические функции перехода и выхода , и памяти, сохраняющей на один такт предыдущее состояние автомата:
Здесь aA, bB, qQ – символы алфавитов в соответствующем временном такте t=1,2,3,…
Автомат Мили.
Автомат Мили (англ. Mealy machine) — конечный автомат, выходная последовательность которого (в отличие от автомата Мура) зависит от состояния автомата и входных сигналов. Это означает, что в графе состояний каждому ребру соответствует некоторое значение (выходной символ). В в вершины графа автомата Мили записываются выходящие сигналы,а дугам графа приписывают условие перехода из одного состояния в другое,а так же входящие сигналы. Кодировка автомата Мили: Вершина (операторная или логическая),стоящая после вершины "Начало" ,а так же вход вершины "Конец" помечается символом S1,вершины,стоящие после операторных помечаются символом Sn (n=2,3..).
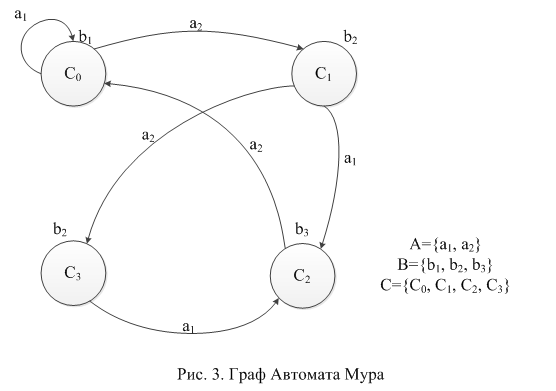
2)Автомат Мура.
Зависимость выходного сигнала только от состояния представлена в автоматах типа Мура (англ. Moore machine). В автомате Мура функция выходов определяет значение выходного символа только по одному аргументу — состоянию автомата. Эту функцию называют также функцией меток, так как она каждому состоянию автомата ставит метку на выходе.
Представление автоматов с помощью графов.
Граф автомата –
это ориентированный связный граф,
вершины которого символизируют внутренние
состояния автомата, а дуги – переходы
из одного состояния в другое.
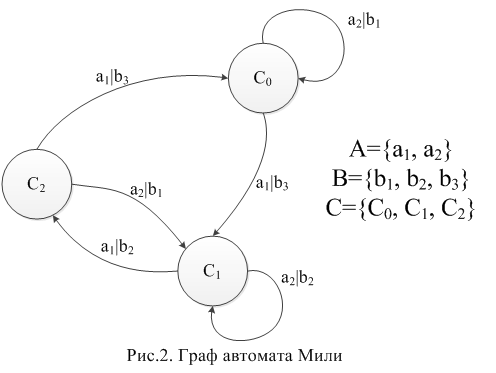 Для
графа Мили на дугах указываются сходные
и выходные буквы. Выходные буквы пишутся
над дугами, символизируя то, что выходное
состояние зависит от состояния автомата
в предыдущий момент времени.
Для
графа Мили на дугах указываются сходные
и выходные буквы. Выходные буквы пишутся
над дугами, символизируя то, что выходное
состояние зависит от состояния автомата
в предыдущий момент времени.
3)Основы анализа логических схем с обратными связями.
Особенностью логических схем с обратными связями является зависимость состояния выходов схемы как от входных переменных в данном такте, так и от входных переменных, действовавших в предыдущем такте. Поэтому такая схема может быть рассмотрена как последовательностное устройство, как конченый автомат.
Схема с обратными связями может находиться в устойчивом состоянии или в неустойчивом состоянии. Неустойчивое состояние схемы будет такое, в котором схема находится короткое время. Наличие в схеме двух и более устойчивых состояний указывает на то, что схема может быть использована для запоминания некоторых входных значений переменных.
4)Анализ логических схем с помощью карт Карно.
Карты Карно (КК) можно рассматривать как развертки геометрических кубов на плоскости. Карта Карно, предназначенная для задания и минимизации функций n переменных, имеет 2n клеток. Каждая клетка соответствует набору переменных. В тех клетках, которые соответствуют значениям функции, равным 1, записываются единицы, а в остальных – нули (или вместо нулей оставляются пустые клетки).
Разметка карт. Разметка предназначена для установления взаимно однозначного соответствия между наборами ЛФ и клетками. Начнем с n = 2:


 или
или 
Соседние наборы различаются только одной координатой
n = 3: n = 4 (даны два варианта возможной разметки):



Пример заполнения карты и минимизации для n = 3.
. ƒ(x1, x2,
x3)
ƒ(x1, x2,
x3)
Исходная функция:
f =
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (Са = 12, Сb
= 16). Соседние клетки, заполненные
единицами, можно объединить в контур,
используя 2к соседних клеток.
Каждому контуру будет соответствовать
конъюнктивный терм ДНФ. Результат
минимизации: f =
(Са = 7, Сb
= 10).
(Са = 12, Сb
= 16). Соседние клетки, заполненные
единицами, можно объединить в контур,
используя 2к соседних клеток.
Каждому контуру будет соответствовать
конъюнктивный терм ДНФ. Результат
минимизации: f =
(Са = 7, Сb
= 10).
5) RS-триггер на элементах “И-НЕ”. Анализ с помощью таблицы Карно и переходов.
Т риггером
(Т) называют логическую схему с
положительной обратной связью, имеющую
два устойчивых состояния, которые
называются единичным
и нулевым
и обозначаются 1 и 0. Перевод триггера в
единичное состояние путем воздействия
на его входы называют установкой
(set)
триггера, а устанавливающий сигнал и
вход, на который он воздействует,
обозначают S
(от set).
Перевод триггера в нулевое состояние
называют сбросом
(reset),
а соответствующий сигнал и вход обозначают
R.
риггером
(Т) называют логическую схему с
положительной обратной связью, имеющую
два устойчивых состояния, которые
называются единичным
и нулевым
и обозначаются 1 и 0. Перевод триггера в
единичное состояние путем воздействия
на его входы называют установкой
(set)
триггера, а устанавливающий сигнал и
вход, на который он воздействует,
обозначают S
(от set).
Перевод триггера в нулевое состояние
называют сбросом
(reset),
а соответствующий сигнал и вход обозначают
R.
Схема простейшего триггера (рис.4.1,а) получается, если включить кольцом два элемента И-НЕ. Такой триггер имеет два входа R и S, два выхода Q и называется RS-триггером. Его обозначение на функциональных схемах показано на рис. 4.1, б.
а) б) в)
Рис.4.1. RS-триггер на элементах И-НЕ
Пока на обоих управляющих входах R и S уровни сигналов не активны, в данном случае R=S=1, триггер находится в каком-либо одном из двух устойчивых состояний. Если значение сигнала на выходе Q равно 1, то, как видно из схемы, этот единичный сигнал, поступая по цепи обратной связи на вход элемента 2, вызывает появление на выходе сигнала с нулевым уровнем. В свою очередь нулевой уровень выхода , поступая на вход элемента 1, поддерживает Q в состоянии 1. Иначе говоря, при входных сигналах R и S, равных 1, появившаяся по любой причине на выходе Q единица по цепи обратной связи будет сама себя поддерживать сколь угодно долго. Когда на прямом выходе Q сигнал равен 1, говорят, что триггер находится в состоянии 1 или что он установлен.
В силу симметрии схемы она будет столь же устойчива в своем противоположном - нулевом состоянии, когда Q =0, а =1. В этом случае говорят, что триггер сброшен. Режим RS-триггера, когда оба управляющих сигнала R и S неактивны, называют режимом хранения.
На рис. 4.1,в показана временная диаграмма переходных процессов в схеме при подаче на нее управляющих сигналов. Исходное состояние триггера - нулевое, на его входы поступают по очереди сначала сигнал S, затем, после его окончания - сигнал R.
Из диаграммы видно, что после окончания входного сигнала триггер способен сохранять свое новое состояние также сколь угодно долго. Говорят, что триггер запоминает входной сигнал. Это специфическое и очень важное свойство триггера, отличающее его от всех рассмотренных ранее схем, не имевших обратных связей: после исчезновения входного сигнала выходной сигнал в тех схемах также исчезал.
Если на входы R и S подать одновременно нулевые сигналы, то на обоих выходах Q и появятся единицы . Если теперь одновременно снять нули со входов R и S, то оба элемента начнут переключаться в нулевое состояние, каждый стремясь при этом оставить своего партнера в состоянии 1. Какой элемент одержит в этом поединке победу, будет зависеть от скоростей переходных процессов и ряда других неизвестных заранее факторов. Для разработчика схемы результирующее состояние триггера оказывается неопределенным, неуправляемым. Поэтому комбинация R=S=0 считается запрещенной, и в обычных условиях ее не используют. Такую комбинацию допустимо применять, лишь когда обеспечено не одновременное, а строго поочередное снятие R и S-сигналов.
Основное назначение триггеров в цифровых схемах - хранить выработанные логическими схемами результаты. Для отсечения еще не установившихся, искаженных переходными процессами результатов между выходом логической схемы и входом триггера можно включить конъюнкторы, управляемые синхросигналом . Это решение оказалось очень эффективным, быстро стало типовым и побудило изготовителей триггеров ввести конъюнкторы в состав триггера. Так появились синхронные триггеры, которые переключаются в состояние, предписываемое управляющими входами, лишь по сигналу синхронизации, поступающему на вход С триггера.

а) б)
Рис. 4.2. Синхронный RS-триггер
Схема простейшего синхронного RS-триггера показана на рис.4.2,а. При С=0 триггер 3-4 отключен от управляющих S и R входов и находится в режиме хранения ранее полученной информации. При С=1 схема функционирует как обычный RS-триггер. Условное изображение синхронного RS-триггера показано на рис.4.2,б. Синхровход С может в принципе иметь и активный низкий уровень; в этом случае он, как обычно, помечается кружочком. Характерной особенностью схемы является то, что в течение всего отрезка времени, когда синхросигнал равен 1, как сами потенциалы на управляющих S и R входах, так и любые их изменения тут же передаются на выход.
О такой схеме можно сказать, что она прозрачна по S - и R - входам при C=1. Не все схемы синхронных триггеров обладают этим свойством.
6) RS-триггер на элементах “ИЛИ-НЕ”. Анализ с помощью таблицы Карно и переходов.
