
- •7. Теорема Больцано-Вейерштрасса
- •Доказательство:
- •Замечание
- •Интересно знать:
- •10. Непрерывность функции в точке
- •2) Частная производная
- •§ 4. Дифференцируемость функции нескольких переменных
- •1. Дифференцируемые функции нескольких переменных.
- •15. Теорема (о дифференцировании сложной функции)
- •Доказательство
- •16. Теоремы о дифференцируемых функциях
- •18. Производные и дифференциалы высших порядков
- •19. Производная по направлению
- •Связь с градиентом
19. Производная по направлению
У этого термина существуют и другие значения, см. Производная.
В математическом анализе, производная по направлению — это обобщение понятия производной на случайфункции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.
Производная функции одной переменной показывает, как изменяется её значение при малом изменении аргумента. Если мы попытаемся по аналогии определить производную функции многих переменных, то столкнёмся с трудностью: в этом случае изменение аргумента (то есть точки в пространстве) может происходить в разных направлениях, и при этом будут получаться разные значения производной. Именно это соображение и приводит к определению производной по направлению.
Рассмотрим
функцию ![]() от
от ![]() аргументов
в окрестности точки
аргументов
в окрестности точки ![]() .
Для любогоединичного
вектора
.
Для любогоединичного
вектора ![]() определим
производную функции
в
точке
определим
производную функции
в
точке ![]() по
направлению
по
направлению ![]() следующим
образом:
следующим
образом:
![]()
Значение этого выражения показывает, как быстро меняется значение функции при сдвиге аргумента в направлении вектора .
Если направление сонаправленно с координатной осью, то производная по направлению совпадает с частной производной по этой координате.
Связь с градиентом
Производную по направлению дифференцируемой по совокупности переменных функции можно рассматривать как проекцию градиента функции на это направление, или иначе, как скалярное произведение градиента на орт направления:
![]()
Отсюда следует, что максимальное значение в точке производная по направлению принимает, если направление совпадает с направлением градиента функции в данной точке
21.
Точка ![]() называется точкой
локального максимума функции
называется точкой
локального максимума функции ![]() ,
если существует такая окрестность этой
точки, что для всех
,
если существует такая окрестность этой
точки, что для всех ![]() из
этой окрестности выполняется
неравенство:
из
этой окрестности выполняется
неравенство: ![]() .
.
Точка
называется точкой
локального минимума функции
,
если существует такая окрестность этой
точки, что для всех
из
этой окрестности ![]()
Т
е о р е м а 1. Пусть ![]() -
стационарная точка функции
-
стационарная точка функции ![]() (т.
е.
(т.
е. ![]() )
и
имеет
вторую непрерывную производную в
окрестности
.
Тогда:
)
и
имеет
вторую непрерывную производную в
окрестности
.
Тогда:
если ![]() ,
то
есть
точка локального максимума
;
,
то
есть
точка локального максимума
;
если
же ![]() ,
то
есть
точка локального минимума
.
,
то
есть
точка локального минимума
.
Д
о к а з а т е л ь с т в о. Разложим
по
формуле Тейлора по степеням ![]() при
при ![]() .
Так как
.
Так как ![]() ,
то формула Тейлора функции
в
окрестности точки
имеет
вид
,
то формула Тейлора функции
в
окрестности точки
имеет
вид
 .
(2)
.
(2)
В
этой формуле может быть ![]() .
.
Пусть
.
Так как производная ![]() по
условию непрерывна в окрестности
по
условию непрерывна в окрестности ![]() ,
то найдется
,
то найдется ![]() такое,
что
такое,
что
![]() .
.
Но тогда остаточный член в формуле (2)
 ,
,
что показывает, что
![]() .
.
т. е. имеет в локальный максимум.
Аналогично,
если
,
то ![]() в
некоторой окрестности
и
в
некоторой окрестности
и ![]() .
Поэтому остаточный член формулы (2) в
окрестности
неотрицательный,
а вместе с ним и
.
Поэтому остаточный член формулы (2) в
окрестности
неотрицательный,
а вместе с ним и ![]() ,
т. е.
имеет
в
локальный
минимум.
,
т. е.
имеет
в
локальный
минимум.
2)
Экстремумом
функции называется
максимальное (минимальное) значение
функции на заданном множестве. Точка,
в которой достигается экстремум
называется точкой
экстремума.
Точка
называется
точкой локального
максимума функции ![]() ,
если выполняется условие:
,
если выполняется условие: ![]()
![]()
![]() Аналогично
точка
называется
точкой локального
минимумафункции
,
если выполняется условие:
Аналогично
точка
называется
точкой локального
минимумафункции
,
если выполняется условие:
![]()
Точки, в которых производная равна нулю, называютсястационарными точками. Точки, в которых функция непрерывна, а её производная либо равна нулю, либо не существует, называются критическимиточками.
Теорема (необходимое условие экстремума)
Если точка — точка экстремума функции , то она критическая.
Доказательство
По
условию точка
—
точка экстремума функции
![]() по
теореме Ферма производная
по
теореме Ферма производная ![]() точка
является
критической.
точка
является
критической.
Пример:
Найти
экстремум функции ![]()
![]() .
Найдем
производную этой функции:
.
Найдем
производную этой функции:![]() критические
точки задаются уравнением
критические
точки задаются уравнением ![]() .
Корни этого уравнения
.
Корни этого уравнения ![]() и
и ![]() .
.
Как
видно по рисунку функция имеет максимум
в точке 1, а минимум в точке 3.
Подставим
эти значения чтобы убедиться в исходную
функцию: ![]()
![]() и
и ![]() в
точке
функция
имеет минимум, равный -4, а в точке
функция
имеет максимум, равный 0.
в
точке
функция
имеет минимум, равный -4, а в точке
функция
имеет максимум, равный 0.
Замечания:
Не всякая критическая точка является точкой экстремума.
22. Теорема (первое достаточное условие экстремума в терминах первой производной)
Пусть функция определена и дифференцируема в некоторой окрестности точки , кроме, быть может, самой точки и непрерывна в этой точке. Тогда:
Если производная
 меняет
знак с «-» на «+» при переходе через
точку
:
меняет
знак с «-» на «+» при переходе через
точку
: 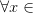
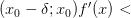
 и
и
 ,
то
—
точка строго минимума функции
,
то
—
точка строго минимума функции
Если производная меняет знак с «+» на «-» при переходе через точку :
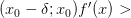 и
и
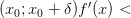 ,
то
—
точка строго максимума функции
,
то
—
точка строго максимума функции
Доказательство
Пусть,
например,
меняет
знак с «-» на «+». Рассмотрим точку
на
сегменте ![]() Воспользуемся
теоремой о конечных приращениях
Лагранжа:
Воспользуемся
теоремой о конечных приращениях
Лагранжа: ![]()
![]() ,
, ![]() .
Поскольку при переходе через точку
функция
меняет знак с «-» на «+», то
.
Поскольку при переходе через точку
функция
меняет знак с «-» на «+», то ![]() и
и ![]() ,
то
,
то ![]()
![]() Аналогично
рассмотрим сегмент
Аналогично
рассмотрим сегмент ![]() ,
получим
,
получим
![]()
![]() —
точка строгого минимума функции.
—
точка строгого минимума функции.
Замечания:
Если
—
точка строго экстремума, то из этого не
следует, что производная ![]() меняет
знак при переходе через точку
меняет
знак при переходе через точку ![]()
Теорема (второе достаточное условие строгого экстремума в терминах второй производной)
Пусть
дана функция
,
она определена в некоторой окрестности
точки
, ее
первая производная
и
пусть ![]() ,
тогда:
,
тогда:
Если
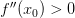 ,
то точка
—
точка строгого минимума;
,
то точка
—
точка строгого минимума;Если
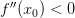 ,
то точка
—
точка строгого максимума.
,
то точка
—
точка строгого максимума.
Доказательство
Докажем
теорему для первого случая, когда
.
По скольку ![]() непрерывна,
то на достаточно малом интервале
непрерывна,
то на достаточно малом интервале ![]() ,
т.к
,
то
,
т.к
,
то ![]() возрастает
в этом интервале.
,
значит
возрастает
в этом интервале.
,
значит ![]() на
интервале
на
интервале ![]() и
и ![]() на
интервале
на
интервале ![]() .
Таким
образом функция
убывает
на интервале
и
возрастает на интервале
по
первому достаточному условию экстремума
функция в точке
имеет
минимум.
Аналогично доказывается
второй случай теоремы.
.
Таким
образом функция
убывает
на интервале
и
возрастает на интервале
по
первому достаточному условию экстремума
функция в точке
имеет
минимум.
Аналогично доказывается
второй случай теоремы.
Замечания:
Если ![]() и
и ![]() ,
то функция
может
и не иметь экстремум в точке
,
то функция
может
и не иметь экстремум в точке
Теорема (третье достаточное условие строгого экстремума в терминах производных порядка больше двух)
Пусть
функция
определена
в некоторой окрестности точки
,
и в этой точке существуют производные
до n-го порядка пусть ![]() ,
, ![]() и
и ![]()
![]() ,
, ![]() Тогда:
Тогда:
Если
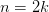 (т.е
(т.е  —
четное), то
—
точка экстремума:
—
четное), то
—
точка экстремума:если
 ,
то
—
точка локального максимума;
,
то
—
точка локального максимума;если
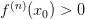 ,
то
—
точка локального минимума;
,
то
—
точка локального минимума;
Если
 (т.е
—
нечетное), то
—
не является точкой экстремума.
(т.е
—
нечетное), то
—
не является точкой экстремума.
Доказательство
Воспользуемся
формулой Тейлора в окрестности точки
с
остатком в форме Пеано: ![]()
![]()
![]()
![]()
![]() .
По
скольку все производные до
.
По
скольку все производные до ![]() порядка
включительно равны нулю получим:
порядка
включительно равны нулю получим: ![]()
![]()
![]() Запишем
полученное выражение в виде:
Запишем
полученное выражение в виде:
![]()
![]() .
Выражение
.
Выражение ![]() .
Пусть
.
Пусть
![]() ,
, ![]()
![]() .
Отсюда следует, что сохранение или
изменение знака приращения функции во
время перехода через точку
зависит
от четности
.
Последний факт и доказывает теорему
.
Отсюда следует, что сохранение или
изменение знака приращения функции во
время перехода через точку
зависит
от четности
.
Последний факт и доказывает теорему
23.
Определение ряда и его сходимость |
Определение 1. Пусть задана бесконечная числовая последовательность u1, u2,…,un,…. Выражение
называется числовым рядом. Числа u1, u2,…,un,… называются первым, вторым, …, n-м, … членами ряда. un также называется общим членом ряда. Определение 2. Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда:
Определение
3. Если
существует конечный предел |
§2. Простейшие свойства числовых рядов |
Теорема 1. Если сходится ряд, полученный из ряда (1) отбрасыванием нескольких его членов, то сходится и ряд (1). Обратно, если сходится данный ряд (1), то сходится ряд, полученный из ряда (1) отбрасыванием нескольких членов. Другими словами: на сходимость ряда не влияет отбрасывание конечного числа его членов. Доказательство. Пусть Sn – n-я частичная сумма ряда (1), Ck – сумма к отброшенных членов (заметим, что при достаточно большом n все отброшенные члены содержатся в сумме Sn), n-k – сумма членов ряда, входящих в сумму Sn и не входящих в Ck. Таким образом:
где Ck – постоянное число, не зависящее от n.
Из
последнего равенства следует, что
если существует
Теорема 2. Если ряд (1) сходится и его сумма равна S, то ряд
где с – число, также сходится и его сумма равна c.S. Доказательство. Пусть Sn и n – n-е частичные суммы соответственно рядов (1) и (2). Тогда
Предел n существует, так как
Теорема 3. Если ряды
и
сходятся
и их суммы равны соответственно
и
(u1-v1)+
(u2-v2)+…+
(un-vn)+…
также
сходятся и их суммы равны
соответственно
Доказательство.
Докажем сходимость ряда (4).
Обозначим n, n=(u1+v1)+(u2+v2)+…+(un+vn)=(u1+u2+…+un)+ +(v1+v2+…+vn)= + Sn. Переходя в этом равенстве к пределу при n, получим
= Таким образом, ряд (4) сходится и его сумма равна + S. Аналогично доказывается, что ряд (5) сходится и его сумма равна -S. Сделайте это самостоятельно. |
2)
Критерий Коши.(необходимые и достаточные условия сходимости ряда) |
|
|
|
Для
того, чтобы последовательность
1.3
Определение. Ряд Теорема. (Критерий Коши равномерной сходимости ряда) Для равномерной сходимости ряда Необходимо и достаточно, чтобы для любого числа e>0 существовал такой номер N(e), что при n>N и любом целом p>0 неравенство
Выполнялось бы для всех х на отрезке [a, b]. Теорема. (Признак равномерной сходимости Вейерштрасса) (Карл Теодор Вильгельм Вейерштрасс (1815 – 1897) – немецкий математик) Ряд Сходится равномерно и притом абсолютно на отрезке [a, b], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами :
Т. е. имеет место неравенство:
Еще
говорят, что в этом случае функциональный
ряд
мажорируется
числовым рядом Ряд Интегральный признак Коши. Если
j(х) – непрерывная положительная
функция, убывающая на промежутке
[1;¥), то ряд j(1) + j(2) + …+ j(n) + … = Пример.
Ряд Следствие.
Если f(x) и j(х) – непрерывные функции
на интервале (a, b] и |
24.


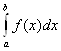 и
и  ведут
себя одинаково в смысле сходимости.
ведут
себя одинаково в смысле сходимости.