
- •7. Теорема Больцано-Вейерштрасса
- •Доказательство:
- •Замечание
- •Интересно знать:
- •10. Непрерывность функции в точке
- •2) Частная производная
- •§ 4. Дифференцируемость функции нескольких переменных
- •1. Дифференцируемые функции нескольких переменных.
- •15. Теорема (о дифференцировании сложной функции)
- •Доказательство
- •16. Теоремы о дифференцируемых функциях
- •18. Производные и дифференциалы высших порядков
- •19. Производная по направлению
- •Связь с градиентом
1)
Несобственные интегралы первого рода
Определение Предположим,
что функция ![]() задана
на бесконечном промежутке вида
задана
на бесконечном промежутке вида![]() и
интегрируема на любом конечном отрезке
и
интегрируема на любом конечном отрезке ![]() ,
где
,
где ![]() .
Таким образом, можно рассмотреть функцию,
зависящую от верхнего предела, как от
переменной:
.
Таким образом, можно рассмотреть функцию,
зависящую от верхнего предела, как от
переменной:
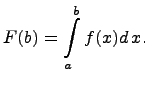
Если
эта функция имеет предел при ![]() ,
то число
,
то число ![]() называется значением
несобственного интеграла первого рода:
называется значением
несобственного интеграла первого рода:
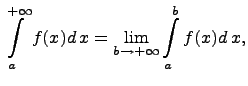
а сам определенный интеграл называется сходящимся. Если же предела не существует, то интеграл называется расходящимся и не имеет никакого числового значения.
Если
функция ![]() определена
и непрерывна на всей числовой прямой,
то может существовать несобственный
интеграл данной функции с двумя
бесконечными пределами интегрирования,
определяющийся формулой:
определена
и непрерывна на всей числовой прямой,
то может существовать несобственный
интеграл данной функции с двумя
бесконечными пределами интегрирования,
определяющийся формулой:
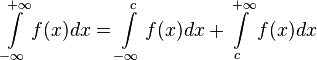 ,
где с — произвольное число.
,
где с — произвольное число.
Геометрический смысл несобственного интеграла I рода
Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.
2)
Определение. Подпоследовательность ![]() называется последовательностью
Коши или фундаментальной,
если
называется последовательностью
Коши или фундаментальной,
если ![]()
Критерий Коши сходимости последовательности
Для того, чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она былафундаментальной.
Доказательство
Необходимость:
Пусть
последовательность имеет конечный
предел. Докажем, что она является
фундаментальной.
Пусть ![]() по
определению предела последовательности:
по
определению предела последовательности: ![]()
Поскольку ![]() произвольное,
то мы можем взять вместо него, к
примеру,
произвольное,
то мы можем взять вместо него, к
примеру, ![]() :
:
![]()
![]() То
есть:
То
есть: ![]() ,
а значит,
,
а значит, ![]() —
фундаментальная по определению.
Необходимость
доказана.
—
фундаментальная по определению.
Необходимость
доказана.
Достаточность:
Пусть
— фундаментальная
последовательность. Докажем, что она
имеет конечный предел. Сначала
покажем,
что ![]() — ограничена.
Поскольку
— фундаментальная последовательность,
то по определению фундаментальной
последовательности:
— ограничена.
Поскольку
— фундаментальная последовательность,
то по определению фундаментальной
последовательности:
![]() и
и ![]()
![]()
Так
как
произвольное,
то возьмем ![]()
![]()
![]()
![]()
![]() —
ограничена.
—
ограничена.
По теореме
Больцано-Вейерштрасса последовательность
имеет сходящуюся подпоследовательность ![]()
Пусть ![]() ,
покажем, что число a и
будет пределом всей
последовательности
:
Поскольку
фундаментальная:
,
покажем, что число a и
будет пределом всей
последовательности
:
Поскольку
фундаментальная:
![]()
![]()
Так
как ![]() сходящаяся:
сходящаяся:
![]()
![]()
![]() Возьмём
Возьмём ![]() ,
тогда:
,
тогда:
Достаточность доказана.
2.

3. Для исследования сходимости и расходимости несобственных интегралов применяется признак сравнения:
Пусть
функция f(x)
и g(x)
удовлетворяют неравенству: ![]() и
несобственный интеграл
и
несобственный интеграл  сходится.
Тогда сходится и несобственный интеграл
сходится.
Тогда сходится и несобственный интеграл  .
.
Доказательство: В
силу сходимости
по
критерию Коши для функции ![]() ,
выполняется неравенство
,
выполняется неравенство  .
Но тогда, ввиду неравенств:
.
Но тогда, ввиду неравенств: ![]() аналогично
неравенство будет справедливо и для
функции f(x),
т.е.
аналогично
неравенство будет справедливо и для
функции f(x),
т.е.

Следовательно, по критерию Коши существует предел:
 ,
т.е. этот интеграл сходится.
,
т.е. этот интеграл сходится.
Замечание1: Аналогичный признак сравнения справедлив и для несобственных интегралов 2 рода.
Замечание2: Отрицанием признака сравнения будет следующее утверждение: если несобственный интеграл расходится, то расходится и несобственный интеграл .
5.




2) Если каждой паре векторов x, y линейного пространства L поставлено в соответствие действительное число (x, y), так, что для любых x, y и z из L и любого действительного числаα справедливы следующие аксиомы:
(x, y) = (y, x),
(α·x, y) = α·(x, y),
(x + y, z) =(x, z) + (y, z),
(x, x)> 0 при x ≠ 0, (0, 0) = 0,
то в пространстве L определено скалярное произведение (x, y).
Если в линейном пространстве определено скалярное произведение, то такое пространство называется евклидовым пространством.
В математике термин евклидово пространство может обозначать один из двух сходных объектов:
1.
Конечномерное вещественное векторное
пространство ![]() с
введённой на нём нормой
с
введённой на нём нормой

где ![]() .
Также назывется конечномерным гильбертовым
пространством
.
Также назывется конечномерным гильбертовым
пространством
2. Метрическое пространство, которое является конечномерным векторным пространством над полем вещественных чисел с метрикой, введённой по формуле:

где
и ![]()
Наглядными
примерами евклидовых пространств могут
служить пространства ![]() размерности n =
1 (вещественная прямая) и
размерности n =
1 (вещественная прямая) и ![]() размерности n =
2 (комплексная плоскость или евклидова
плоскость).
размерности n =
2 (комплексная плоскость или евклидова
плоскость).
Ещё один вариант определения евклидово пространства


3)
|
|
|
|
Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т. д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников. Множества обычно обозначают большими буквами: A, B, C, N, ..., а элементы этих множеств − аналогичными маленькими буквами: a, b, c, n, ... Существуют стандартные обозначения для некоторых множеств. Например,
 −
множество целых чисел;
−
множество целых чисел; −
множество рациональных
чисел;
−
множество рациональных
чисел; −
множество иррациональных
чисел;
−
множество иррациональных
чисел;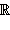 −
множество действительных
чисел;
−
множество действительных
чисел; −
множество комплексных
чисел.
−
множество комплексных
чисел.
Если
элемент a принадлежит
множеству A,
то пишут: a ![]() A.
A.
Множество считается заданным, если для любого объекта можно определить, принадлежит ли этот объект множеству или нет.
Множество,
не содержащее ни одного элемента,
называется пустым
множеством и
обозначается ![]() Если A есть
пустое множество, то пишут: A =
Если A есть
пустое множество, то пишут: A =
Если
любой элемент множества A является
элементом другого множества B,
то говорят, что A есть подмножество множества B,
и пишут:A ![]() B.
B.
Например,
множество всех натуральных чисел ![]() является
подмножеством всех действительных
чисел
является
подмножеством всех действительных
чисел ![]() Из
определения непосредственно следует,
что A
A,
то есть всякое множество является
подмножеством самого себя.
Из
определения непосредственно следует,
что A
A,
то есть всякое множество является
подмножеством самого себя.
|
Если A B, а B A, то пишут A = B и говорят, что множества A и B равны. |
4) Область определения функции — множество, на котором задаётся функция
Если задана функция, которая действует из одного множества в другое, то множество, из которого действует данная функция, называется областью определения.
Более
формально, пусть задано отображение ![]() ,
которое отображает множество
,
которое отображает множество ![]() в
в ![]() ,
то есть:
,
то есть: ![]() ;
тогда
;
тогда
множество называется областью определения функции
и обозначается
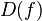 ,
или
,
или 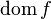 (от
англ. domain «область»).
(от
англ. domain «область»).
Обычно
предполагается, что ![]() ,
из-за чего понятие области определения
выглядит тавтологией: «область определения
функции — это область, где определена
функция». Для того, чтобы придать чёткий
смысл данному понятию, рассматривается
некоторое более широкое множество,
которое бывает областью
отправления,
и тогда область
определения функции
,
из-за чего понятие области определения
выглядит тавтологией: «область определения
функции — это область, где определена
функция». Для того, чтобы придать чёткий
смысл данному понятию, рассматривается
некоторое более широкое множество,
которое бывает областью
отправления,
и тогда область
определения функции ![]() —
это такое подмножество множества
(которое
и есть область отправления функции),
где для каждого элемента
—
это такое подмножество множества
(которое
и есть область отправления функции),
где для каждого элемента ![]() определено
значение функции
определено
значение функции ![]() .
.
Этот
факт коротко записывают в виде: ![]() .
.
6.
7. Теорема Больцано-Вейерштрасса
Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность .
Доказательство:
![]() Предположим,
что
Предположим,
что ![]() -
ограниченна, тогда все члены
последовательности принадлежат
некоторому отрезку
-
ограниченна, тогда все члены
последовательности принадлежат
некоторому отрезку ![]() .
Разделим
пополам.
Мы получим два отрезка. Хотя бы один из
них содержит бесконечное число членов
последовательности. Выберем этот
отрезок. Если оба обладают этим свойством,
то выберем первый. Выбранный отрезок,
который содержит бесконечное число
членов данной последовательности,
обозначим
.
Разделим
пополам.
Мы получим два отрезка. Хотя бы один из
них содержит бесконечное число членов
последовательности. Выберем этот
отрезок. Если оба обладают этим свойством,
то выберем первый. Выбранный отрезок,
который содержит бесконечное число
членов данной последовательности,
обозначим ![]() и
его длина равна
и
его длина равна ![]() .
Разделим отрезок
.
Разделим отрезок ![]() пополам,
выберем из двух получившихся
отрезков
пополам,
выберем из двух получившихся
отрезков ![]() длина
которого
длина
которого ![]() Продолжая
эти рассуждения, мы получим последовательность
отрезков
Продолжая
эти рассуждения, мы получим последовательность
отрезков ![]() таких,
что:
таких,
что:
Следовательно,
по определению, наша
последовательность ![]() стягивающаяся Тогда,
по теореме
Кантора,
существует единственная точка С,
принадлежащая всем отрезкам, то
есть:
стягивающаяся Тогда,
по теореме
Кантора,
существует единственная точка С,
принадлежащая всем отрезкам, то
есть:
![]() (1)
Покажем,
что
(1)
Покажем,
что ![]() Так
как отрезок
содержит
бесконечное число членов последовательности
,
то
Так
как отрезок
содержит
бесконечное число членов последовательности
,
то ![]() .
Отрезок
.
Отрезок ![]() также
содержит бесконечное число членов
данной последовательности, и
поэтому:
также
содержит бесконечное число членов
данной последовательности, и
поэтому:
![]() Вообще,
Вообще, ![]() ,
где
,
где ![]() Следовательно,
существует
подпоследовательность
Следовательно,
существует
подпоследовательность ![]() последовательности
такая,
что
последовательности
такая,
что ![]() (2)
Условия (1) и (2) означают,
что точка С и
принадлежат
отрезку
(2)
Условия (1) и (2) означают,
что точка С и
принадлежат
отрезку ![]() ,
и поэтому расстояние между ними не
превосходит длины отрезка
,
и поэтому расстояние между ними не
превосходит длины отрезка ![]() то
есть:
при
то
есть:
при ![]() По теореме о
трех последовательностях
По теореме о
трех последовательностях
![]() Теорема
доказана
Теорема
доказана ![]()
Замечание
Теорему Больцано-Вейерштрасса можно сформулировать еще и так: любая ограниченная последовательность имеет хотя бы один частичный предел.
Интересно знать:
Метод, примененный в доказательстве данной теоремы ,который состоит в последовательном делении пополам рассматриваемых промежутков, называется методом Больцано, он часто используется при доказательстве других теорем.
Теорему о трех последовательностях называют также теорема о двух милиционерах. Название теоремы происходит из того факта, что если два милиционера держат между собой преступника и при этом идут в камеру, то заключённый также вынужден туда идти. В разных странах её называют по-разному: теорема сжатия, теорема о сэндвиче (или правило сэндвича), теорема о трёх струнах, теорема о двух жандармах, теорема о двух городовых и пр.
8.



9.



10. Непрерывность функции в точке
Пусть функция f(x) определена в некоторой окрестности O(x0) точки x0 (включая саму точку x0).
Функция f(x) называется непрерывной в точке x0, если существует limx → x0 f(x) , равный значению функции f(x) в этой точке:
|
f(x) = f(x0), |
(1) |
т.е.
|
O( f(x0) ) O(x0) : x O(x0) f(x) O( f(x0) ) . |
|
Замечание. Равенство (1) можно записать в виде:
|
f(x) = f (
x ), |
|
т.е. под знаком непрерывной функции можно переходить к пределу.
Пусть Δx = x − x0 — приращение аргумента, Δy = f(x) − f(x0 ) — соответствующее приращение функции.
Необходимое и достаточное условие непрерывности функции в точке
Функция y = f(x) непрерывна в точке х0 тогда и только тогда, когда
|
Δy = 0. |
(2) |
Замечание. Условие (2) можно трактовать как второе определение непрерывности функции в точке. Оба определения эквивалентны.
Пусть функция f(x) определена в полуинтервале [x0, x0 + δ ).
Функция f(x) называется непрерывной справа в точке x0, если существует односторонний предел
|
f(x) = f(x0). |
|
Пусть функция f(x) определена в полуинтервале (x0 − δ, x0].
Функция f(x) называется непрерывной слева в точке x0, если существует односторонний предел
|
f(x) = f(x0). |
|
Непрерывность суммы, произведения и частного двух непрерывных функций
Теорема 1. Если функции f(x) и g(x) непрерывны в точке х0, то в этой точке непрерывны
|
f(x) ± g(x), f(x) · g(x),
(g(x0) ≠ 0). |
|
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 59.
Непрерывность сложной функции
Теорема 2. Если функция u(x) непрерывна в точке х0, а функция f(u) непрерывна в соответствующей точке u0 = f(x0), то сложная функция f(u(x)) непрерывна в точке х0.
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 59.
Все элементарные функции непрерывны в каждой точке их областей определения.
Локальные свойства непрерывных функций
Теорема 3 (ограниченность непрерывной функции). Если функция f(x) непрерывна в точке x0, то существует окрестность O(x0), в которой f(x) ограничена.
Доказательство следует из утверждения об ограниченности функции, имеющей предел.
Свойства непрерывных функций.
1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.
2)
Частное двух непрерывных функций ![]() –
есть непрерывная функция при условии,
что g(x)
не равна нулю в точке х0.
–
есть непрерывная функция при условии,
что g(x)
не равна нулю в точке х0.
3) Суперпозиция непрерывных функций – есть непрерывная функция.
Это свойство может быть записано следующим образом:
Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.
Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.
11.

12.

13. Приращение функции При сравнении значения функции f в некоторой фиксированной точке x0 со значениями этой функции в различных точках x, лежащих в окрестности x0, удобно выражать разность f(x) – f(x0) через разность x – x0, пользуясь понятиями «приращение аргумента» и «приращение функции» . Пусть x – произвольная точка, ледащая в некоторой окрестности фиксированной точки x0. разность x – x0 называется приращение независимой переменной ( или приращением аргумента) в точке x0 и обозначается Δx. Таким образом, Δx = x –x0, откуда следует, что x = x0 + Δx. Говорят также, что первоначальное значение аргумента x0 получило приращение Δx. Вследствие этого значение функции f изменится на величину f(x) – f(x0) = f (x0 +Δx) – f(x0). Эта разность называется приращением функции f в точке x0, соответствующим приращению Δx, и обозначается символом Δf (читается «дельта эф») , т. е. по определению Δf = f (x0 + Δx) – f (x0), откуда f (x) = f (x0 +Δx) = f (x0) + Δf. При фиксированном x0 приращение Δf есть функция от Δx. Δf называют также приращение зависимой переменной и обозначают через Δy для функции y = f(x) .
Другое определение :
Приращение
функции
в
точке ![]() —
функция, обычно обозначаемая
—
функция, обычно обозначаемая ![]() от
новой переменной
от
новой переменной ![]() ,
определяемая как
,
определяемая как
![]()
Переменная называется приращением аргумента.
В случае, когда ясно о каком значении идёт речь, применяется более короткая запись.
![]()
Говорят, что первоначальное значение аргумента получило приращение
 .
Вследствие этого значение функции
получило
приращение
.
Вследствие этого значение функции
получило
приращение
![]()
